Polygones et constructions : corrigé des exercices de maths en 6ème en PDF
Mis à jour le 23 novembre 2025
Exercice 1 – recopier et compléter.
a. Dans le triangle GFH, [GH] est le côté opposé au sommet F.
b. Dans le triangle DHE, E est le sommet opposé au côté [DH].
c. Dans le triangle FEH, [FE] est le côté opposé au sommet H.
d. Dans le triangle EGD, E est le sommet opposé au côté [GD].
Exercice 2 – reproduire les figures.
Réponse a :
Pour dessiner le quadrilatère VETR :
– VT = 3,5 cm
– VE = 2,5 cm
– ET = 4,2 cm
– ER = 4 cm
– TR = 3 cm
Réponse b :
Pour dessiner le trapèze REOU :
– ER = 5,3 cm
– EU = 6,2 cm
– OU = 7 cm
Sachant que les segments RG et OG sont égaux, il faut alors respecter les longueurs et angles donnés pour les reproduire fidèlement.
Exercice 3 – construction de triangles.
Triangle ABC :
Construis un triangle avec les longueurs suivantes :
AB = 3,5 cm, AC = 3 cm, BC = 4 cm.
Triangle DEF :
Construis un triangle avec les longueurs suivantes :
DE = 4,2 cm, DF = 4,8 cm, EF = 4 cm.
Triangle GHI :
Construis un triangle avec les longueurs suivantes :
GH = 6,5 cm, HI = 3,7 cm, GI = 5 cm.
Utilise la méthode du compas et de la règle, en laissant les traits de construction apparents pour chaque triangle.
Exercice 4 – reproduire chaque figure.
a. S, T et W sont alignés.
Pour reproduire la figure, on doit respecter les longueurs et les angles indiqués.
- Tracer la droite STW de sorte que ST = 4,5 \, cm.
- Placer U tel que UT = 3,8 ,cm et les segments SU et SV sont égaux avec la même notation des traits.
- Placer V tel que les segments UT et VT sont égaux avec la même notation des traits.
b. ADE est rectangle en E, BDE est équilatéral et CDE est isocèle en D.
- Tracer le rectangle ADE avec EA = 2 ,cm et ED = 5 , cm.
- Placer B tel que le triangle BDE soit équilatéral, donc BD = DE.
- Placer C tel que le triangle CDE soit isocèle en D, donc CD = DE.
Exercice 5 – donner le nom des quadrilatères.
– Quadrilatère ABCD : Parallélogramme (côtés opposés parallèles).
– Quadrilatère EFGH : Parallélogramme (côtés opposés parallèles).
– Quadrilatère IJKL : Losange (tous les côtés de même longueur).
– Quadrilatère MNOP : Trapèze (une paire de côtés parallèles).
– Quadrilatère QRST : Trapèze (une paire de côtés parallèles).
Exercice 6 – les lunules d’Hippocrate.
Pour reproduire la figure à l’échelle, nous devons d’abord dessiner le triangle ABC avec les dimensions données :
AB = 6 cm, BC = 8 cm et AC = 10 cm.
Ensuite, traçons les demi-cercles :
- Un demi-cercle sur AB de diamètre AB = 6 cm.
- Un demi-cercle sur BC de diamètre BC = 8 cm.
- Un demi-cercle sur AC de diamètre AC = 10 cm.
La lunule d’Hippocrate est l’ensemble des parties colorées entre les deux demi-cercles sous le segment [AC].
Pour vérifier le processus de construction des lunules géométriquement, notez que la somme des aires des deux lunules est égale à l’aire du triangle
ABC .
Calcul de l’aire du triangle ABC en utilisant la formule de Héron :
Le semi-périmètre s est donné par :

L’aire du triangle est :
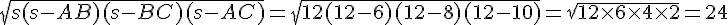
La somme des aires des deux lunules est donc égale à l’aire du triangle, confirmant la propriété des lunules d’Hippocrate.
Exercice 7 – des quadrilatères.
a. Donne la nature de chaque quadrilatère. Justifie.
Quadrilatère ABCD : C’est un losange car tous ses côtés sont égaux (3 cm) et ses diagonales sont perpendiculaires (indiqué par l’angle droit au centre).
Quadrilatère EFGH : C’est un rectangle car ses angles sont droits et ses côtés opposés sont égaux (3 cm et 5 cm).
Quadrilatère JKLM : C’est un carré car tous ses côtés sont de même longueur (7 cm) et tous ses angles sont droits.
Quadrilatère PQRS : C’est un trapèze car il a une paire de côtés parallèles (indiqué par les côtés PQ et SR avec les mesures données).
b. Construis chacun de ces quadrilatères en vraie grandeur.
Pour construire ces quadrilatères :
1. Losange ABCD : Trace un segment de 4,5 cm pour représenter une diagonale. Trace une autre diagonale perpendiculaire de 3 cm. Connecte les points d’intersection pour former le losange.
2. Rectangle EFGH : Trace un côté de 3 cm. À chaque extrémité, trace un angle droit et prolonge de 5 cm pour former l’autre côté. Connecte pour former le rectangle.
3. Carré JKLM : Trace un côté de 7 cm. À chaque extrémité, trace un angle droit, prolonge chaque côté de 7 cm et connecte pour fermer le carré.
4. Trapèze PQRS : Trace un côté de 4 cm. Trace une diagonale PS de 1 cm. Trace un côté parallèle à PS de longueur 7 cm. Complète le trapèze en connectant les extrémités restantes.
Exercice 8 – construction de triangle et parallèles
a. Tracer un triangle ABC.
b. À partir du point A, tracer une droite (d) parallèle à la droite (BC).
À partir du point B, tracer une droite (d’) parallèle à la droite (AC); elle coupe (d) en E.
À partir du point C, tracer une droite (d ») parallèle à la droite (AB); elle coupe (d) en F et (d’) en G.
c. Tracer les droites (EC), (BF) et (AG).
Observation : Les droites (EC), (BF) et (AG) se coupent en un même point, appelé le centre du triangle de Ronce.
Exercice 9 – donner la nature d’un triangle
a. Le triangle 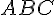
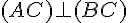
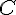
b. Le triangle 

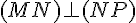
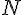
c. Le triangle 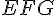
Exercice 10 – construction de triangles.
1. Triangle ABC :
Il s’agit d’un triangle isocèle en A avec AB = AC = 5 cm et BC = 4 cm. Les angles à la base sont égaux.
2. Triangle DEF :
Il s’agit d’un triangle isocèle en E avec DE = DF et EF = 6 cm. L’angle 
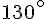
3. Triangle GHI :
Il s’agit d’un triangle équilatéral avec chaque côté de 4 cm.
Tous les angles mesurent 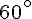
4. Triangle JKL :
Il s’agit d’un triangle rectangle en L avec JL = 5 cm et KL = 6 cm.
En utilisant le théorème de Pythagore, calculons JK :

5. Triangle PQR :
Il s’agit d’un triangle rectangle isocèle en Q avec QR = PQ = 4 cm.
Calculons PR en utilisant le théorème de Pythagore :
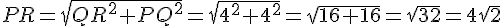
Télécharger ou imprimer cette fiche «polygones et constructions : corrigé des exercices de maths en 6ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.





