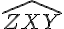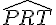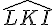Bissectrice d’un angle : corrigé des exercices de maths en 6ème en PDF

Mis à jour le 23 novembre 2025

La bissectrice d’un angle est un concept fondamental en géométrie, essentiel pour les élèves de sixième. Comprendre ce concept permet de développer des compétences clés en maths, telles que la construction géométrique et la mesure des angles. Cet article propose des corrections d’exercices pratiques qui aideront les élèves à maîtriser ce sujet, offrant ainsi une base solide pour leur parcours scolaire. Suivez nos conseils pour exceller dans l’étude de la bissectrice et améliorer votre confiance en mathématiques !

Exercice 1 – construction de la bissectrice d’un angle.

Pour construire la bissectrice d’un angle, suivez ces étapes pour chaque angle donné :

1. Angle $\widehat{xOy}$ de 48°:

$\frac{48}{2}=24$

Utilisez votre rapporteur pour tracer la bissectrice de l’angle $\widehat{xOy}$ , qui est de 24 ° à partir de la demi-droite [Ox).

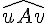
2. Angle $\widehat{uAv}$ de 94°:

$\frac{94}{2}=47$

Utilisez votre rapporteur pour tracer la bissectrice de l’angle $\widehat{xOy}$ , qui est de 47 ° à partir de la demi-droite [Au).

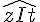
3. Angle $\widehat{zIt}$ de 32° :

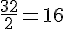
$\frac{32}{2}=16$

Utilisez votre rapporteur pour tracer la bissectrice de l’angle $\widehat{xOy}$ , qui est de 16 ° à partir de la demi-droite [Iz).

Exercice 2 – construction des bissectrices d’un triangle.

Pour construire les bissectrices d’un triangle ABC, voici les étapes :

1. Construction de la bissectrice de l’angle A :

Placez la pointe du compas sur le point A. Tracez un arc qui coupe les côtés AB et AC. Marquez les points d’intersection comme D et E.

Ensuite, placez la pointe du compas sur D et tracez un petit arc à l’intérieur de l’angle. Répétez cela avec la pointe sur E, de telle sorte que les deux arcs se coupent à un point F.

Tracez une droite de A passant par F. Cette droite est la bissectrice de l’angle A.

2. Construction de la bissectrice de l’angle B :

Placez la pointe du compas sur le point B. Tracez un arc qui coupe les côtés BA et BC. Marquez les points d’intersection comme G et H.

Ensuite, placez la pointe du compas sur G et tracez un petit arc à l’intérieur de l’angle.

Répétez cela avec la pointe sur H, de telle sorte que les deux arcs se coupent à un point I.

Tracez une droite de B passant par I. Cette droite est la bissectrice de l’angle B.

3. Construction de la bissectrice de l’angle C :

Placez la pointe du compas sur le point C. Tracez un arc qui coupe les côtés CA et CB.

Marquez les points d’intersection comme J et K.

Ensuite, placez la pointe du compas sur J et tracez un petit arc à l’intérieur de l’angle.

Répétez cela avec la pointe sur K, de telle sorte que les deux arcs se coupent à un point L.

Tracez une droite de C passant par L. Cette droite est la bissectrice de l’angle C.

4. Intersection des bissectrices :

Les trois bissectrices se rencontrent en un même point, appelé le centre du cercle inscrit du triangle.

Exercice 3 – tracer un angle et construire la bissectrice.

a. Tracer un angle de 40° :

1. Tracez une demi-droite horizontale à partir d’un point O .

2. À l’aide du rapporteur, mesurez et tracez un angle de 40 ° en positionnant le centre du rapporteur sur le point O.

3. Tracez une deuxième demi-droite partant de O qui passe par le point marqué pour obtenir l’angle de 40 °.

Construction de la bissectrice :

1. Placez la pointe du compas sur le point Oet tracez un arc qui coupe les deux demi-droites de l’angle.

2. Marquez les points où l’arc coupe les demi-droites comme A et B.

3. Sans changer l’ouverture du compas, tracez deux arcs, l’un centré en A et l’autre en B, qui se croisent à un point C .

4. Tracez la demi-droite [OC). Cela représente la bissectrice de l’angle 40 °.

b. Tracer un angle de 100 ° :

1. Tracez une demi-droite horizontale à partir d’un point O.

2. Avec le rapporteur, mesurez et tracez un angle de 100 °.

3. Tracez une deuxième demi-droite qui passe par le point marqué.

Construction de la bissectrice : Suivez les mêmes étapes pour la construction de la bissectrice comme en a.

c. Tracer un angle de 170 ° :

1. Tracez une demi-droite horizontale à partir d’un point O.

2. Utilisez le rapporteur pour mesurer un angle de 170 °.

3. Tracez une deuxième demi-droite qui passe par le point marqué.

Construction de la bissectrice : Répétez les étapes pour la bissectrice comme en a et b.

Exercice 4 – construction d’un triangle et des bissectrices.

Etapes de construction :

1. Tracer le triangle EFG :

a. Dessiner le segment EF.

b. Dessiner le segment FG.

c. Dessiner le segment GE pour fermer le triangle.

2. Construire la bissectrice de l’angle E :

a. Avec le compas, tracer un arc de cercle centré en E qui coupe les segments EF et EG en deux points.

b. Sans changer l’ouverture du compas, tracer des arcs de cercle centrés sur chaque point d’intersection.

c. Tracer la droite passant par E et le point d’intersection des deux arcs. C’est la bissectrice de l’angle E.

3. Construire la bissectrice de l’angle F :

Répéter les étapes précédentes en utilisant le point F comme centre.

4. Construire la bissectrice de l’angle G :

Répéter les étapes précédentes en utilisant le point G comme centre.

Conclusion : Les trois bissectrices se rencontrent en un seul point appelé l’orthocentre du triangle.

Exercice 5 – angles et bissectrices.

1. Tracer un angle 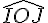$\widehat{IOJ}$ de 80°.

Utilisez un rapporteur pour tracer précisément un angle de 80° en partant du point O.

2. Construire sa bissectrice (d) avec la règle et le compas.

– Placez la pointe sèche du compas sur le sommet O et tracez un arc qui coupe les côtés [OI]et [OJ] de l’angle.

– Notez les points d’intersection A et B.

– Sans modifier l’ouverture du compas, tracez un arc à partir de A et un autre à partir de B pour qu’ils se coupent en un point C.

– Tracez la droite (d) passant par O et C. C’est la bissectrice de l’angle 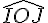$\widehat{IOJ}$ .

3. On note K le point d’intersection de la droite (d) et du segment [IJ].

Pour ce faire, prolongez la bissectrice si nécessaire jusqu’à ce qu’elle coupe le segment [IJ], et notez cette intersection K.

4. Mesurer les angles $\widehat{IOK}$ et $\widehat{KOJ}$ avec le rapporteur.

Chacun de ces angles devrait mesurer 40°, car une bissectrice divise un angle en deux angles égaux.

Le résultat était-il prévisible ?

Oui, le résultat est prévisible car une bissectrice divise toujours un angle en deux parties égales. Ainsi, l’angle initial de 80° est divisé en deux angles de 40° chacun.

Exercice 6 – construire la bissectrice d’un angle donné.

a. 20° :

1. Tracer un angle de 20° avec le rapporteur.

2. Placer la pointe sèche du compas sur le sommet de l’angle et tracer un arc de cercle qui coupe les deux côtés de l’angle.

3. Appeler les points d’intersection obtenus B et C.

4. Sans changer l’écartement du compas, tracer un arc à partir de B et un autre à partir de C, les deux arcs se coupent en un point D.

5. Tracer le segment du sommet de l’angle à D. C’est la bissectrice.

b. 70° :

1. Tracer un angle de 70° avec le rapporteur.

2. Placer la pointe sèche du compas sur le sommet de l’angle et tracer un arc de cercle qui coupe les deux côtés de l’angle.

3. Appeler les points d’intersection obtenus E et F.

4. Sans changer l’écartement du compas, tracer un arc à partir de E et un autre à partir de F, les deux arcs se coupent en un point G.

5. Tracer le segment du sommet de l’angle à G. C’est la bissectrice.

c. 90° :

1. Tracer un angle de 90° avec le rapporteur.

2. Placer la pointe sèche du compas sur le sommet de l’angle et tracer un arc de cercle qui coupe les deux côtés de l’angle.

3. Appeler les points d’intersection obtenus H et I.

4. Sans changer l’écartement du compas, tracer un arc à partir de H et un autre à partir de I, les deux arcs se coupent en un point J.

5. Tracer le segment du sommet de l’angle à J. C’est la bissectrice.

d. 150° :

1. Tracer un angle de 150° avec le rapporteur.

2. Placer la pointe sèche du compas sur le sommet de l’angle et tracer un arc de cercle qui coupe les deux côtés de l’angle.

3. Appeler les points d’intersection obtenus K et L.

4. Sans changer l’écartement du compas, tracer un arc à partir de K et un autre à partir de L, les deux arcs se coupent en un point M.

5. Tracer le segment du sommet de l’angle à M. C’est la bissectrice.

Exercice 7 – déterminer les bissectrices.

La demi-droite rouge semble être la bissectrice de l’angle dans les figures :

Une bissectrice est une ligne qui divise un angle en deux angles égaux. Dans les figures a, c et d, la demi-droite rouge semble partager l’angle de manière égale de chaque côté.

Exercice 8 – indiquer quelle droite est la bissectrice.

Réponse a : La bissectrice est la demi-droite bleue.

Réponse b : La bissectrice est la demi-droite orange.

Exercice 9 – construire la bissectrice des angles.

1. Construction de la bissectrice de l’angle WXY :

– A l’aide d’un compas, trace un arc de cercle centré en X qui coupe les côtés WX et XY, ce qui nous donne les points A et B.

– Sans changer l’ouverture du compas, trace deux arcs de cercle à partir des points A et B pour qu’ils se croisent en un point C.

– La droite XC est la bissectrice de l’angle WXY.

2. Construction de la bissectrice de l’angle WZY :

– A partir du point Z, trace un arc de cercle qui coupe les côtés WZ et ZY aux points D et E.

– Avec la même ouverture, trace deux arcs à partir des points D et E qui se croisent au point F.

– La droite ZF est la bissectrice de l’angle WZY.

Exercice 10 – tracer un angle et la bissectrice.

Réponse a :

Trace un angle 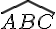$\widehat{ABC}$ = 32 °. Pour tracer sa bissectrice :

Place la pointe sèche du compas sur le sommet B et trace un arc qui coupe les côtés de l’angle en deux points distincts, notons-les D et E.
Sans changer l’ouverture du compas, trace deux arcs à partir de D et E qui se croisent en un point F.
Trace la droite (BF). La droite (BF) est la bissectrice de l’angle $\widehat{ABC}$ .

Réponse b :

Un angle 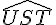$\widehat{UST}$ = 180 ° est un angle plat.
La bissectrice d’un angle plat est la droite elle-même.

Réponse c :

Trace un angle 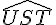$\widehat{UST}$ = 67 °.

Pour tracer la bissectrice :

1. Place la pointe sèche du compas sur le sommet X et trace un arc qui coupe les côtés de l’angle en deux points distincts, notons-les G et H.
2. Sans changer l’ouverture du compas, trace deux arcs à partir de G et Hqui se croisent en un point I.
3. Trace la droite (XI). La droite (XI) est la bissectrice de l’angle $\widehat{ZXY}$ .

Réponse d :

Trace un angle

$\widehat{WZD}$ = 90 °.

Pour tracer la bissectrice :

1. Place la pointe sèche du compas sur le sommet Z et trace un arc qui coupe les côtés de l’angle en deux points distincts, notons-les J et K.
2. Sans changer l’ouverture du compas, trace deux arcs à partir de J et K qui se croisent en un point L.
3. Trace la droite (ZL). La droite (ZL) est la bissectrice de l’angle $\widehat{WZD}$ .

Réponse e :

Trace un angle

$\widehat{PRT}$ = 127 °.

Pour tracer sa bissectrice :

Place la pointe sèche du compas sur le sommet R et trace un arc qui coupe les côtés de l’angle en deux points distincts, notons-les M et N.
Sans changer l’ouverture du compas, trace deux arcs à partir de M et N qui se croisent en un point O.
Trace la droite (RO). La droite (RO) est la bissectrice de l’angle $\widehat{PRT}$ .

Réponse f :

Trace un angle

$\widehat{LKI}$ = 154 °.

Pour tracer sa bissectrice :

Place la pointe sèche du compas sur le sommet K et trace un arc qui coupe les côtés de l’angle en deux points distincts, notons-les P et Q.
Sans changer l’ouverture du compas, trace deux arcs à partir de P et Q qui se croisent en un point R.
Trace la droite (KR). La droite (KR) est la bissectrice de l’angle $\widehat{LKI}$ .

Voter.. post

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «bissectrice d'un angle : corrigé des exercices de maths en 6ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

La division euclidienne et décimale

Aires et périmètres de figures

Statistiques et gestion de données

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 330 034 cours et exercices de maths téléchargés en PDF et 4 250 exercices.