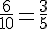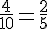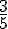Probabilités : corrigé des exercices de maths en 3ème en PDF

Mis à jour le 23 novembre 2025

Les probabilités sont un domaine essentiel des maths enseigné en classe de troisième, qui permet aux élèves de développer des compétences cruciales en analyse et en raisonnement. Comprendre les concepts fondamentaux des probabilités aide non seulement à résoudre des exercices variés, mais aussi à construire une base solide pour des études futures. Dans cet article, nous allons proposer des corrections d’exercices de mathématiques axées sur les probabilités, permettant ainsi aux élèves de maîtriser cette notion clé et d’améliorer leur performance académique.

Exercice 1 – les probabilités

1) Déterminer la probabilité de l’événement :

a. « on gagne 2 € » :

Il y a 1 secteur gris parmi 8 secteurs. Donc, la probabilité est 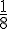$\frac{1}{8}$ .

b. « on gagne 1 € » :

Il y a 1 secteur noir parmi 8 secteurs. Donc, la probabilité est 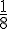$\frac{1}{8}$ .

c. « on perd 2 € » :

Il y a 2 secteurs blancs parmi 8 secteurs. Donc, la probabilité est 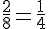$\frac{2}{8}=\frac{1}{4}$ .

2) A-t-on autant de chances de gagner que de perdre ? Justifier.

Pour gagner, il faut gagner 1 € ou 2 €.

Probabilité de gagner 1 € : 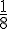$\frac{1}{8}$ .

Probabilité de gagner 2 € : 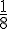$\frac{1}{8}$ .

La probabilité de gagner (1 € ou 2 €) est donc : 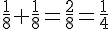$\frac{1}{8}+\frac{1}{8}=\frac{2}{8}=\frac{1}{4}$ .

Pour perdre, il faut soit perdre 1 € ou 2 €.

Probabilité de perdre 1 € : 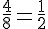$\frac{4}{8}=\frac{1}{2}$ .

Probabilité de perdre 2 € : 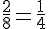$\frac{2}{8}=\frac{1}{4}$ .

La probabilité de perdre est donc : 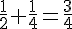$\frac{1}{2}+\frac{1}{4}=\frac{3}{4}$ .

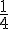
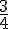
Conclusion : La probabilité de gagner est $\frac{1}{4}$ , tandis que celle de perdre est $\frac{3}{4}$ . Donc, on a moins de chances de gagner que de perdre.

Exercice 2 – probabilités dans une urne

1) Lettre inscrite sur la boule :

a. Issues : A, B, C, D, E, F, G, H, I, J.

b. Non, toutes les issues ont la même probabilité de se produire.

c. Oui, il s’agit d’une situation d’équiprobabilité.

d. Probabilités :

Lettre C : $\frac{1}{10}$
Lettre I : $\frac{1}{10}$
Voyelle : A, E, I donc $\frac{3}{10}$

2) Couleur de la boule :

a. Issues : Blanche, Noire.

b. Non, chaque couleur a la même probabilité de se produire.

c. Oui, il s’agit d’une situation d’équiprobabilité.

d. Probabilités :

Boule blanche : A, B, E, F, I, J donc $\frac{6}{10}=\frac{3}{5}$
Boule noire : C, D, G, H donc $\frac{4}{10}=\frac{2}{5}$

3) Couleur et lettre :

a. Oui, situation d’équiprobabilité.

b. Probabilités :

Blanche : $\frac{3}{5}$
Avec une voyelle : $\frac{3}{10}$
Blanche avec une voyelle : A, E, I donc $\frac{3}{10}$
Blanche ou avec une voyelle : A, B, E, F, I, J donc $\frac{6}{10}=\frac{3}{5}$

Exercice 3 – prendre en compte des informations.

1. Quels sont les différents codes possibles ?

Il y a 3 lettres (A, B, C) et 3 chiffres (1, 2, 3), donc le nombre total de codes possibles est :

$3\times 3=9$

Les codes possibles sont : A1, A2, A3, B1, B2, B3, C1, C2, C3.

2a. Quelle probabilité a-t-elle d’obtenir le bon code ?

Il y a un seul bon code parmi les 9 possibles, donc la probabilité est :

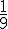
$\frac{1}{9}$

2b. Quelle probabilité a-t-elle de trouver le bon code à son deuxième essai ?

En se trompant à la fois de lettre et de chiffre, elle élimine complètement le code A1 qu’elle a testé. Il reste donc 8 codes possibles. La probabilité de trouver le bon code au deuxième essai est alors :

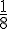
$\frac{1}{8}$

2c. Justifier que, lors de ce deuxième essai, Anna ne se trompe que de lettre, elle est sûre de pouvoir ouvrir la porte lors d’un troisième essai.

Si, lors du deuxième essai, Anna ne se trompe que de lettre, elle connaît maintenant le bon chiffre. Il ne lui reste qu’à essayer les deux autres lettres pour trouver le bon code. Elle est donc sûre de réussir au maximum en 3 essais.

Exercice 4 – comparer une fréquence et une probabilité.

a. Le nombre de lancers donnant la somme 7 est de 170.

La fréquence en pourcentage de ces lancers est :
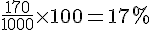
$\frac{170}{1000}\times 100=17\%$

b. Pour obtenir une somme égale à 7 avec deux dés, les combinaisons possibles sont : (1,6), (2,5), (3,4), (4,3), (5,2), (6,1).

Il y a 6 possibilités.

La probabilité d’obtenir cette somme est donc :
$\frac{6}{36}=\frac{1}{6}$ soit environ $16,67\%$

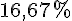
Comparer : La fréquence obtenue dans la simulation (17%) est proche de la probabilité théorique (16,67%).

Exercice 5 – comprendre un programme.

a. Le programme affecte à la variable A la valeur 1 si n < 9, et 0 sinon.

– Pour n = 2, n = 3 : A = 1

– Pour n = 10, n = 9, n = 15 : A = 0

b. Les issues possibles de l’expérience aléatoire sont A = 1 et A = 0. Il y a 8 nombres possibles pour n tels que n < 9 (1 à 8), et 7 nombres pour n \geq\, 9 (9 à 15).

– La probabilité que A = 1 : 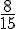$\frac{8}{15}$

– La probabilité que A = 0 : 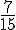$\frac{7}{15}$

Exercice 6 – appliquer un programme.

Analyse :

Dans ce programme, la variable n prend une valeur aléatoire entre 1 et 10 :

A est calculé par : A = 5 + n
B est calculé par : B = 2 \times n

Nous cherchons la probabilité que A = B, donc :

5 + n = 2 \times n

Résolvons l’équation :

5 + n = 2n

5 = 2n – n

5 = n

La seule valeur possible pour n est donc 5.

n peut aller de 1 à 10, donc il y a 10 valeurs possibles.

La probabilité que A = B est donc :

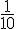
$\frac{1}{10}$

Exercice 7 – probabilités et crayons.

1.a Compléter l’arbre :

– Pour chaque couleur du toit (B, R, J), il y a trois choix possibles pour la couleur de la porte (B, R, J). Ensuite, pour chaque combinaison, il y a encore trois choix possibles pour la couleur de la fenêtre (B, R, J).

1.b Nombre de dessins colorés possibles :

Il y a trois choix pour chaque élément (toit, porte, fenêtre), donc le nombre total de combinaisons possibles est :

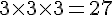
$3\times 3\times 3=27$

2. Calcul de la probabilité :

L’événement 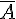$\overline{A}$ est : « L’enfant a utilisé une seule couleur pour les trois éléments ». Il y a 3 manières de tout colorier de la même couleur (BBB, RRR, JJJ).

Donc, la probabilité de 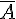$\overline{A}$ est :

$\frac{3}{27}=\frac{1}{9}$

L’événement A est : « L’enfant a utilisé au moins deux couleurs différentes ». La probabilité de A est donnée par :

$1-\frac{1}{9}=\frac{8}{9}$

Exercice 8 – lancer de pièce.

1.a. Compléter l’arbre :

Pour chaque issue du lancer de pièce (Pile ou Face), les couleurs possibles sont : Rouge (R), Vert (V), Bleu (B), Noir (N), et Jaune (J).

1.b. Nombre d’issues : L’expérience compte 2 (Pile, Face) × 5 (couleurs) = 10 issues.

2. Probabilités des événements :

E_1 : « Obtenir la couleur rouge » :

Il y a 2 issues favorables (Pile, Rouge et Face, Rouge) parmi 10 issues possibles, donc :

Probabilité : $\frac{2}{10}=\frac{1}{5}$

E_2 : « Ne pas obtenir la couleur jaune » :

Il y a 8 issues favorables (toutes sauf celles avec Jaune – Pile, Jaune et Face, Jaune) parmi 10 issues possibles, donc :

Probabilité : $\frac{8}{10}=\frac{4}{5}$

Exercice 9 – galettes et probabilités.

1. a. Compléter l’arbre :

Chaque branche de l’arbre indique qui obtient la fève dans chaque galette. Puisque chaque galette peut contenir la fève chez l’un des quatre amis, nous avons pour chaque galette 4 choix possibles. Complétons les branches pour chaque ami (A, B, C, D) pour les deux galettes.

1. b. Nombre d’issues possibles :

Pour chaque galette, il y a 4 possibilités (A, B, C, D). Comme il y a deux galettes et les choix sont indépendants, le nombre total d’issues est :

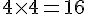
$4\times 4=16$

2. Probabilités :

a. 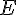$E$ : « Anissa a les deux fèves »

C’est le cas où Anissa (A) obtient la fève dans les deux galettes. Il y a une seule issue favorable : (A, A).

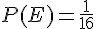
$P(E)=\frac{1}{16}$

b. 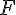$F$ : « Baptiste n’a pas de fève »

Pour Baptiste (B) de ne pas avoir de fève, il ne doit pas être choisi pour aucune des galettes. Il y a 3 possibilités pour chaque galette de ne pas avoir B : (A, C, D). Donc :

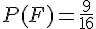
$P(F)=\frac{9}{16}$

c. $G$ : « Coralie a exactement une fève »

Coralie (C) peut avoir la fève soit dans la galette frangipane, soit brioche, mais pas les deux. Il y a deux cas favorables : (C, autre) ou (autre, C).

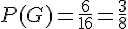
$P(G)=\frac{6}{16}=\frac{3}{8}$

d. 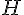$H$ : « Dylan a au moins une fève »

C’est l’événement où Dylan (D) a une fève dans au moins une galette. On soustrait les cas où Dylan n’a pas de fève du total possible :

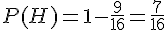
$P(H)=1-\frac{9}{16}=\frac{7}{16}$

Exercice 10 – une roue équilibrée.

1. Liste des issues des événements E, F et G :

– Événement E : « Le numéro repéré est pair. » Les numéros pairs sont : 2, 4, 6, 8, 10.

– Événement F : « Le numéro repéré est multiple de 3. » Les multiples de 3 sont : 3, 6, 9.

– Événement G : « Le numéro repéré est multiple de 5. » Les multiples de 5 sont : 5, 10.

2. Compatibilité des événements :

a. E et F : Ce sont des événements compatibles car il existe un numéro (6) qui est à la fois pair et multiple de 3.

b. E et G : Ce sont des événements compatibles car il existe un numéro (10) qui est à la fois pair et multiple de 5.

c. F et G : Ce sont des événements incompatibles car aucun numéro n’est à la fois multiple de 3 et de 5 (sur la roue, 15 n’existe pas dans les issues).

3. Probabilité de chaque événement :

– Probabilité de E : 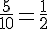$\frac{5}{10}=\frac{1}{2}$

– Probabilité de F : 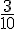$\frac{3}{10}$

– Probabilité de G : $\frac{2}{10}=\frac{1}{5}$

4.8/5 - (32041 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «probabilités : corrigé des exercices de maths en 3ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Arithmétique et décomposition en facteurs premiers

Sections de solides et volumes

Scratch

Les équations

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 373 321 cours et exercices de maths téléchargés en PDF et 4 250 exercices.