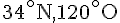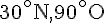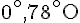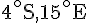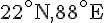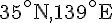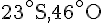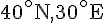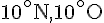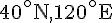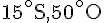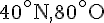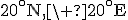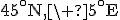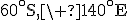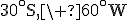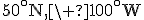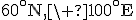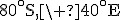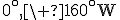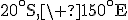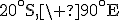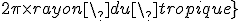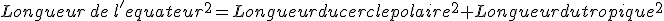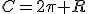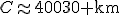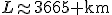Coordonnées géographiques : corrigé des exercices de maths en 3ème en PDF

Mis à jour le 23 novembre 2025

Les coordonnées géographiques jouent un rôle essentiel dans la compréhension des espaces terrestres, un sujet crucial pour les élèves de troisième. Dans cet article, nous allons corriger des exercices de mathématiques qui permettent de développer des compétences fondamentales, telles que la représentation graphique et la localisation sur un plan. Maîtriser ces concepts est indispensable pour réussir dans des domaines variés, allant de la géographie à la navigation. Preuve d’une solide compréhension, ces exercices offriront un atout précieux pour les élèves en quête de succès académique.

Exercice 1 – nom de villes françaises.

1. Rennes est à l’ouest de Paris.

2. Lyon est au Nord de Marseille.

3. Strasbourg est à l’est de Paris.

4. Orléans est au sud de Paris.

Exercice 2 – coordonnées de villes sur le globe terrestre.

1. Quelles sont les villes situées dans l’hémisphère Nord, c’est-à-dire au nord de l’équateur ? Justifier votre réponse.

Les villes situées dans l’hémisphère Nord ont une latitude positive. Ces villes sont :

Abu Dhabi (25^\circ)
Pékin (39^\circ)
Atlanta (33^\circ)

2. Quelles sont les villes situées dans l’hémisphère ouest, c’est-à-dire à l’ouest du méridien de Greenwich ?

Les villes situées dans l’hémisphère ouest ont une longitude négative. Ces villes sont :

Atlanta (\-84^\circ)
Ushuaia (\-19^\circ)

3. Pour chacun des pays suivants, préciser le signe de sa latitude et de sa longitude : USA, Australie, Russie, Argentine.

USA : Latitude positive, longitude négative.
Australie : Latitude négative, longitude positive.
Russie : Latitude positive, longitude positive.
Argentine : Latitude négative, longitude négative.

Exercice 3 – coordonnées géographiques sur le planisphère.

1. a. Repasser en vert le parallèle de latitude $-30^\circ$ . Ce parallèle doit traverser le planisphère à environ un tiers de la distance entre l’équateur et le pôle Sud.

1. b. Repasser en rouge le méridien de longitude 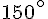$150^\circ$ . Ce méridien doit passer au milieu du Pacifique, proche de la ligne de changement de date.

2. Coordonnées géographiques des villes indiquées :

Los Angeles : $34^\circ\mathrm{N},120^\circ\mathrm{O}$
Nouvelle-Orléans : $30^\circ\mathrm{N},90^\circ\mathrm{O}$
Quito : $0^\circ,78^\circ\mathrm{O}$
Kinshasa : $4^\circ\mathrm{S},15^\circ\mathrm{E}$
Calcutta : $22^\circ\mathrm{N},88^\circ\mathrm{E}$
Moscou : $56^\circ\mathrm{N},38^\circ\mathrm{E}$
Tokyo : $35^\circ\mathrm{N},139^\circ\mathrm{E}$
Sao Paulo : $23^\circ\mathrm{S},46^\circ\mathrm{O}$
Londres : $51^\circ\mathrm{N},0^\circ$

3. Placer les villes suivantes :

Ankara : $40^\circ\mathrm{N},30^\circ\mathrm{E}$
Bamako : $10^\circ\mathrm{N},10^\circ\mathrm{O}$
Kingston : $20^\circ\mathrm{N},80^\circ\mathrm{O}$
Pékin : $40^\circ\mathrm{N},120^\circ\mathrm{E}$
Brasilia : $15^\circ\mathrm{S},50^\circ\mathrm{O}$
Washington : $40^\circ\mathrm{N},80^\circ\mathrm{O}$

Exercice 4 – coordonnées géographiques de points.

1. Sur le schéma, l’équateur est tracé en rouge et le méridien de Greenwich en vert.

2. Coordonnées géographiques des points :

K : 60°N, 60°E
L : 20°N, 80°W
M : 30°S, 40°E
N : 40°S, 20°W

3. Placement des points :

A; 20°S, 10°W
B; 40°N, 30°E
C; 20°S, 10°E
D; 10°S, 30°W

4. Analyse des points :

A et C : Ils ont la même latitude (20°S) mais des longitudes de signes opposés, donc ils sont symétriques par rapport au méridien de Greenwich.
B et D : Ils ont la même longitude (30°) mais des latitudes différentes, situées dans les hémisphères nord et sud, respectivement.

Exercice 5 – temps écoulé entre deux couchers de soleil.

Pourquoi le coucher de soleil à Saint-Claude intervient-il plus tôt qu’à La Rochelle ?

Saint-Claude est situé plus à l’est que La Rochelle (longitude de 5,5 degrés est contre -1,2 degrés ouest). Le Soleil se couche plus tôt à l’est, car la Terre tourne vers l’est.

Calcul du temps écoulé entre les couchers de soleil :

La différence de longitude entre Saint-Claude et La Rochelle est de :

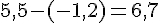
La Terre effectue une rotation complète de 360 degrés en 24 heures, donc elle tourne de :

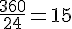
$\frac{360}{24}=15$

degrés par heure.

Le temps écoulé entre les couchers de soleil est donc :

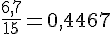
$\frac{6,7}{15}=0,4467$

heures, soit environ 27 minutes.

Conclusion : Le coucher de soleil à Saint-Claude a lieu environ 27 minutes avant celui de La Rochelle.

Exercice 6 – le globe de cristal et coupe du monde de ski.

La ville de Pyeongchang est située approximativement à une latitude de 37° Nord et une longitude de 129° Est.

Exercice 7 – coordonnées géographiques de certaines villes.

1. Étoile : Afrique : $20^\circ\text{N},\ 20^\circ\text{E}$

2. Cercle : Europe : $45^\circ\text{N},\ 5^\circ\text{E}$

3. Cœur : Océanie : $60^\circ\text{S},\ 140^\circ\text{E}$

4. Triangle : Amérique du Sud : $30^\circ\text{S},\ 60^\circ\text{W}$

5. Rectangle : Amérique du Nord : $50^\circ\text{N},\ 100^\circ\text{W}$

6. Ellipse : Asie : $60^\circ\text{N},\ 100^\circ\text{E}$

7. Losange : Antartique : $80^\circ\text{S},\ 40^\circ\text{E}$

8. Soleil : Océan Pacifique : $0^\circ,\ 160^\circ\text{W}$

9. Lune : Océanie : $20^\circ\text{S},\ 150^\circ\text{E}$

10. Nuage : Océan Indien : $20^\circ\text{S},\ 90^\circ\text{E}$

Exercice 8 – latitude et longitude de villes.

1. Lire la latitude de Istanbul, Puerto Montt et Belem :

Istanbul : environ 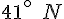$41^\circ\;N$

Puerto Montt : environ 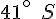$41^\circ\;S$

Belem : environ 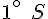$1^\circ\;S$

2. Lire la longitude de Dacca, Londres et Istanbul :

Dacca : environ 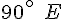$90^\circ\;E$

Londres : environ 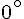$0^\circ$

Istanbul : environ $29^\circ\;E$

3. Placer Saint-Pétersbourg (30° E ; 60° N) :

Saint-Pétersbourg se place légèrement à droite d’Istanbul et plus au nord, vers 60° N de latitude.

Exercice 9 – calculer la longueur du tropique du Capricorne.

1. Calcul de la longueur d’un tropique :

Un tropique est un parallèle, donc sa longueur est donnée par la formule :

$2\pi\times rayon\_du\_tropique}$

Le rayon du tropique est la distance OE. Utilisons le théorème de Pythagore dans le triangle OHE :

$\mathrm{OE}=\sqrt{\mathrm{OH}^2+\mathrm{HE}^2}=\sqrt{6378^2-2543^2}$

Calculons :

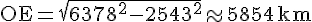
$\mathrm{OE}=\sqrt{6378^2-2543^2}\approx5854\,\text{km}$

La longueur du tropique est alors :

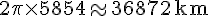
$2\pi\times 5854\approx36872\,\text{km}$

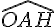
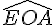
2a. Prouver que $\widehat{OAH}$ et $\widehat{EOA}$ ont la même mesure :

Le triangle OHA est rectangle en H, donc :

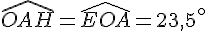
$\widehat{OAH}=\widehat{EOA}=23,5^\circ$

2b. Calculer la longueur du tropique du Capricorne :

Nous avons déjà calculé cette longueur comme étant 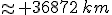$\approx 36872\,km$ .

3a. Calcul d’un cercle polaire :

La latitude d’un cercle polaire est 66,5°. Ainsi, la longueur est :

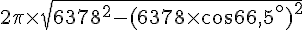
$2\pi\times \sqrt{6378^2-(6378\times \cos66,5^\circ)^2}$

Calculons :

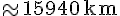
$\approx15940\,\text{km}$

3b. Vérification :

Vérifions que :

$Longueur\,de\,l'equateur^2 = Longueur du cercle polaire^2 + Longueur du tropique^2$

Où l’équateur est :

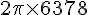
$2\pi\times 6378$

Calculons et comparons :

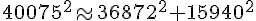
$40075^2\approx36872^2+15940^2$

Les deux côtés de l’équation sont approximativement égaux, vérifiant ainsi la condition donnée.

Exercice 10 – calculer la longueur d’un arc de l’équateur.

1. Calcul de la longueur de l’équateur :

La Terre est considérée comme une sphère de rayon 6 370 km.

La longueur de l’équateur est la circonférence de cette sphère, donnée par la formule :

$C=2\pi R$

En substituant le rayon, on obtient :

$C=2\pi\times 6370$

$C\approx40030\text{ km}$

2. Calcul de la longueur de l’arc AB :

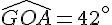
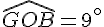
On sait que $\widehat{GOA}=42^\circ$ et $\widehat{GOB}=9^\circ$ .

L’angle total 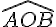$\widehat{AOB}$ est donc :

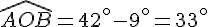
$\widehat{AOB}=42^\circ-9^\circ=33^\circ$

La longueur de l’arc est donnée par :

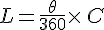
$L=\frac{\theta}{360}\times \,C$

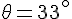
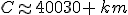
Ici, $\theta=33^\circ$ et $C\approx40030 \,km$ , donc :

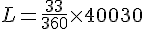
$L=\frac{33}{360}\times 40030$

$L\approx3665\text{ km}$

4.7/5 - (33711 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «coordonnées géographiques : corrigé des exercices de maths en 3ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Fonctions affines

Théorème de Thalès

Généralités sur les fonctions

Trigonométrie

Homothéties

Sections de solides et volumes

Scratch

Calcul littéral

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 373 321 cours et exercices de maths téléchargés en PDF et 4 250 exercices.