Calcul littéral : corrigé des exercices de maths en 3ème en PDF
Mis à jour le 23 novembre 2025
Dans le cadre des mathématiques de troisième, le calcul littéral est une compétence essentielle à maîtriser. Cet article de correction d’exercices vous aidera à comprendre les méthodes et les astuces pour réussir cet aspect fondamental de votre cursus. En développant vos capacités à manipuler les expressions algébriques, vous renforcerez vos connaissances en maths et préparerez efficacement vos examens. Découvrez ici des solutions détaillées qui clarifient ce thème crucial pour votre parcours scolaire.
Exercice 1 – factorisation d’expressions littérales
I. Développement :


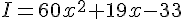
Factorisation :
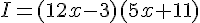
J. Développement :

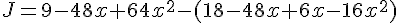

Factorisation :
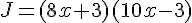
K. Développement :
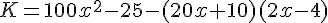
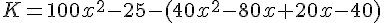
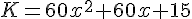
Factorisation :

L. Développement :

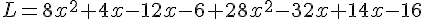
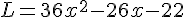
Factorisation :
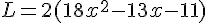
Exercice 2 – développer et réduire – Identités remarquables
A;
Développons l’expression 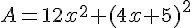
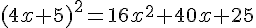
Donc 
Réduction : 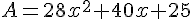
B;
Développons l’expression 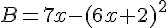
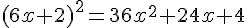
Donc 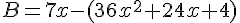
Ce qui donne : 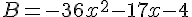
C;
Développons l’expression 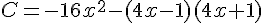
Utilisons la formule de la différence de carrés : 
Donc 
Ce qui donne : 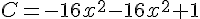
Réduction : 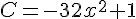
D;
Développons l’expression 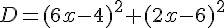
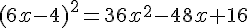
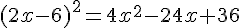
Donc 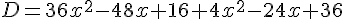
Réduction : 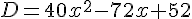
Exercice 3 – calcul littéral.
1. Montre que D s’écrit sous la forme donnée :
Partons de l’expression donnée : 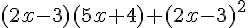
Factorisons par 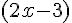

Simplifions l’intérieur de la parenthèse :
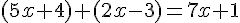
Nous obtenons alors :
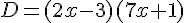
2. Résolution de l’équation 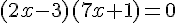
Pour que le produit soit égal à zéro, il faut que l’un des facteurs soit nul :
Premier facteur : 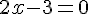
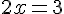
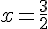
Deuxième facteur : 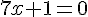
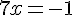
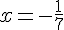
Soluces : 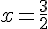
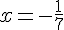
Exercice 4 – calcul littéral-développer et factoriser.
1. Développer puis réduire 
A = (2x – 3)(2x + 3) – (3x + 1)(2x – 3)
Développement :
(2x – 3)(2x + 3) = 4x^2 + 6x – 6x – 9 = 4x² – 9
(3x + 1)(2x – 3) = 6x^2 – 9x + 2x – 3 = 6x² – 7x – 3
Réduction :
A = (4x² – 9) – (6x^2 – 7x – 3) = 4x² – 9 – 6x² + 7x + 3
A = -2x² + 7x – 6
2. Factoriser A .
A = -2x² + 7x – 6
On cherche les racines de l’équation associée :
-2x^2 + 7x – 6 = 0
Discriminant :
Les racines sont :
La factorisation de A est donc :
3. Résoudre l’équation 
On utilise le principe du produit nul :

Pour 
Pour 
Les solutions sont donc 

Exercice 5 – calcul litteral avec les identites remarquables
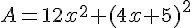
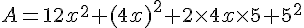

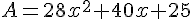
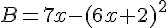

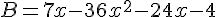
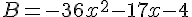

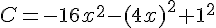
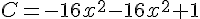
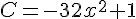
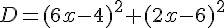
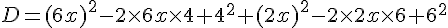
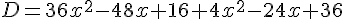
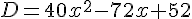
Exercice 6 – aire et identites remarquables
1. Calcul des aires
Première figure :
La grande figure est un carré de côté 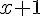
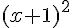
La petite figure blanche à l’intérieur est un carré de côté 1, donc son aire est de 1.
L’aire colorée est donc :
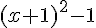
Deuxième figure :
La figure est un rectangle de dimensions 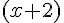


2. Remarque
Nous observons que les deux aires sont égales :
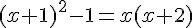
Après simplification, cette égalité revient à une identité remarquable :
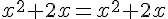
Ce qui est toujours vrai pour tout x.
Exercice 7 – identités remarquables.
A; 
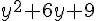
B; 
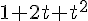
C; 
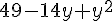
D; 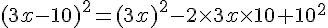
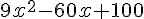
E : 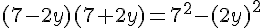
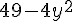
F : 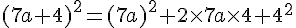
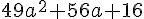
Exercice 8 – développer et réduire.
1. Développer et réduire l’expression B :
On commence par développer chaque partie de l’expression :

Développons 
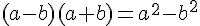
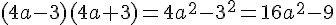
Développons 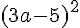
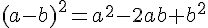
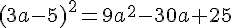
Substituons ces résultats dans l’expression B :
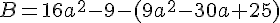
En simplifiant, on obtient :
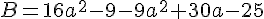
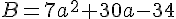
2. Calculer l’expression B pour :
a. a = 1 :
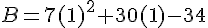
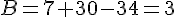
b. a = 0,75 :
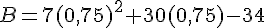
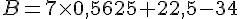
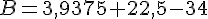
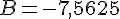
c. a = 0 :
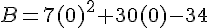
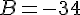
Exercice 9 – calcul numérique.
1. Calcul de 
On utilise l’identité remarquable 
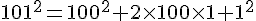
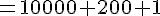

2. Calcul de 
On utilise l’identité remarquable 
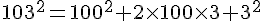
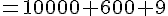
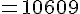
3. Calcul de 
On utilise l’identité remarquable 
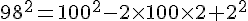
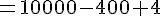

4. Calcul de 
On utilise la formule 
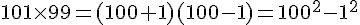


Exercice 10 – développer, réduire et factoriser
1. Développer et réduire l’expression E :
On commence par développer chaque terme :
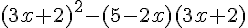
Développons 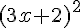
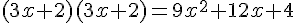
Développons 
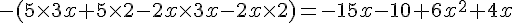
En combinant les termes :
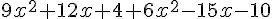
Réduction :
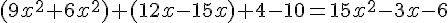
2. Factoriser E :
On cherche à factoriser 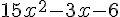
On remarque que le terme commun est 3 :
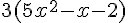
La factorisation du trinôme peut se faire par : 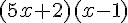
Donc, l’expression factorisée est :
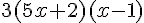
3. Calculer E pour x = -2 :
Remplaçons x par -2 dans l’expression réduite :
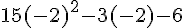
Calcul :
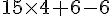

Donc, 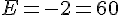
Télécharger ou imprimer cette fiche «calcul littéral : corrigé des exercices de maths en 3ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.












