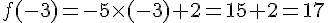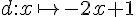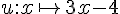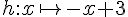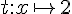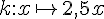Fonctions affines : corrigé des exercices de maths en 3ème en PDF

Mis à jour le 7 avril 2026

Les fonctions affines représentent un concept clé dans le programme de mathématiques de la classe de troisième, essentiel pour développer les compétences analytiques des élèves. Maîtriser ces notions permet d’améliorer la compréhension des equations linéaires et d’appliquer des outils mathématiques dans des situations concrètes. Cet article vous propose des corrections d’exercices pour renforcer vos connaissances et préparer efficacement votre brevet des collèges.

Exercice 1 – les fonctions affines.

a. Les notations $f:x\mapsto3x+7$ et signifient que ce sont des fonctions affines, de la forme ax+b .

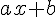
Exercice 2 :

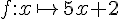
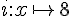
Fonctions affines : $f:x\mapsto5x+2$ , $h:x\mapsto2x$ , $i:x\mapsto8$ , $l:x\mapsto3\sqrt{x}+7$

Fonctions linéaires : $h:x\mapsto2x$

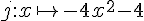
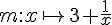
Non affines : $g:x\mapsto-4+3x$ , $j:x\mapsto-4x^{2}-4$ , $k:x\mapsto \frac{3x}{7}$ , $m:x\mapsto3+\frac{1}{x}$

Exercice 3 :

a. Calculer f(2) , f(-3) , f(0) :

$f(2)=-5\times2+2=-10+2=-8$
$f(-3)=-5\times(-3)+2=15+2=17$

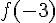
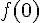
b. Calculer l’image de 4 :

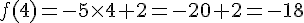
$f(4)=-5\times4+2=-20+2=-18$

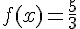
c. Calculer le nombre tel que $f(x)=\frac{5}{3}$ :

$-5x+2=\frac{5}{3}$

$-5x=\frac{5}{3}-2$

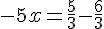
$-5x=\frac{5}{3}-\frac{6}{3}$

$-5x=-\frac{1}{3}$

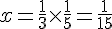
$x=\frac{1}{3}\times\frac{1}{5}=\frac{1}{15}$

Exercice 2 – problème fonction affine et linéaire

1. Reproduire et compléter le tableau :

Nombre de cartouches achetées	2	5	11	14
Prix à payer en magasin en euros	30	75	165	210
Prix à payer par Internet en euros	60	90	150	180

2. Expressions des fonctions :

a. P_A=15x

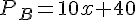
3. Tracer les droites : Les droites d et d’ sont les représentations des fonctions données.

4. Utilisation du graphique :

a. Pour 6 cartouches :

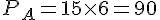
$P_A=15\times6=90$

$P_B=10\times6+40=100$

Il est plus avantageux d’acheter en magasin.

b. Avec 80 euros :

Sonia peut acheter 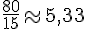$\frac{80}{15}\approx5,33$ cartouches en magasin, soit 5 cartouches.

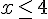
Sur Internet : $10x+40\leq80$ donc $x\leq4$ .

Il est plus avantageux pour elle d’acheter en magasin.

c. Comparaison des prix :

Le prix sur Internet devient inférieur ou égal au prix en magasin lorsque :

5x=40

x=8

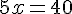
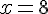
Donc, à partir de 8 cartouches, le prix sur Internet est égal au prix en magasin.

Exercice 3 – fonction affine et volume

1) Montrez que le volume (en m3) de la serre est donné par la formule V = 144 + 16x.

Le volume de la serre est composé du volume du parallélépipède rectangle et du volume de la pyramide qui le surmonte.

Le volume du parallélépipède rectangle est donné par :

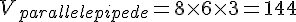
$V_{parallelepipede}=8\times6\times3=144$

Le volume de la pyramide est donné par :

$V_{pyramide}=\frac{1}{3}\times \text{Base}\times \text{Hauteur}=\frac{1}{3}\times (8\times 6)\times x=\frac{48x}{3}=16x$

Donc, le volume total V de la serre est :

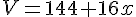
2) Calculez ce volume pour x = 1,5.

En remplaçant x par 1,5 dans l’expression du volume :

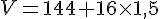
$V=144+16\times1,5$

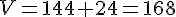
Le volume de la serre pour x = 1,5 est donc de 168 m³.

3) Pour quelle valeur de x le volume de la serre est-il de 200 m³ ?

On résout l’équation suivante :

16x=56

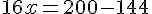
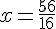
$x=\frac{56}{16}$

x=3,5

La valeur de x pour laquelle le volume de la serre est de 200 m³ est 3,5 mètres.

Exercice 4 – a la recherche de fonctions affines

1) La fonction a une pente de -3 et f(0) = 2, donc elle s’écrit :

2) La fonction s’obtient en ajoutant 6 à x, puis en multipliant par -4, ce qui donne :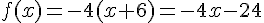

3) La fonction multiplie x par 3, ajoute 4, puis divise par 2, donc : 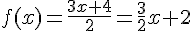$f(x)=\frac{3x+4}{2}=\frac{3}{2}x+2$

4) En développant l’expression donnée : 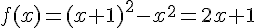$f(x)=(x+1)^{2}-x^{2}=2x+1$

5) La condition d’augmentation implique une pente de 4 et f(0) = 1, d’où :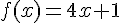

Exercice 5 – fonctions affines, linéaires et problème

1. Expression de A(x) et B(x) :

Avec la formule A : on paie 40 € pour l’adhésion, puis 10 € par mois.

Donc,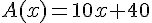

Avec la formule B : on paie 18 € par mois.

Donc,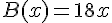

3. Égalité des prix :

a) Du graphique, les prix sont égaux là où les courbes se croisent. Les prix sont les mêmes pour :

40=8x

x=5

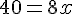
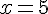
b) Par calcul, on trouve aussi 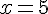x=5

4. Formule la plus avantageuse pour 4 mois :

Pour x = 4 :

Avec la formule A : 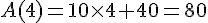$A(4)=10\times4+40=80$

Avec la formule B : 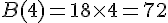$B(4)=18\times4=72$

Pour 4 mois, la formule B est plus avantageuse.

5. Budget de 113 € avec formule A :

On résout 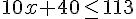$10x+40\leq113$

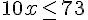
$10x\leq73$

$x\leq7,3$

On peut payer au maximum 7 mois de garderie.

Exercice 6 – fonctions affines, images et antécédents.

1) Soit la fonction affine f définie par f(x) = -2x + 3 .

a) Calculer f(0) . J’ai trouvé x = 3 .

$f(0) = -2 \times 0 + 3 = 3$ . Cela est correct.

b) Calculer l’antécédent de 5.

On résout l’équation -2x + 3 = 5.

L’antécédent de 5 est donc -1 .

2) Soit la fonction affine g telle que g(-2) = -2 et g(3) = 4.

a) Déterminer la fonction g .

La fonction affine s’écrit sous la forme g(x) = ax + b .

Pour x = -2 , g(-2) = -2 = -2a + b .

Pour x = 3 , g(3) = 4 = 3a + b .

Nous avons ainsi deux équations :

En soustrayant la première équation de la seconde :

$a=\frac{6}{5}$

En remplaçant a dans la première équation :
$-2 \times \frac{6}{5} + b = -2$
$-\frac{12}{5} + b = -2$
$b = -2 + \frac{12}{5}$
$b = -\frac{10}{5} + \frac{12}{5}$
$b = \frac{2}{5}$

La fonction $g(x) = \frac{6}{5}x + \frac{2}{5}$ .

b) Calculer g(0) et g(3) .

$g(0) = \frac{6}{5} \times 0 + \frac{2}{5} = \frac{2}{5}$ .

$g(3) = \frac{6}{5} \times 3 + \frac{2}{5} = \frac{18}{5} + \frac{2}{5} = 4$ .
Cela correspond bien à la condition donnée.

3) Dans un même repère $(O, I, J)$.

a) Tracer les représentations graphiques de f et g .

Tracer et $g(x) = \frac{6}{5}x + \frac{2}{5}$ sur le même repère.

b) Calculer les coordonnées du point d’intersection de ces représentations graphiques.

On cherche tel que .
$-2x + 3 = \frac{6}{5}x + \frac{2}{5}$
$-2x - \frac{6}{5}x = \frac{2}{5} - 3$
$-\frac{10}{5}x - \frac{6}{5}x = \frac{2}{5} - \frac{15}{5}$
$-\frac{16}{5}x = -\frac{13}{5}$
$x = \frac{13}{16}$

En remplaçant dans f(x)
= -2 \times \frac{13}{16} + 3 = -\frac{26}{16} + 3 = -\frac{13}{8} + \frac{24}{8} = \frac{11}{8} » class= »LatexImg »>

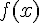
Les coordonnées du point d’intersection sont $(\frac{13}{16}, \frac{11}{8} )$ .

Exercice 7 – tarifs, abonnements et fonctions.

a. Yéro va à la piscine une fois par mois.

Prix pour chaque tarif :

Tarif 1 : €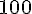

Tarif 2 : 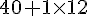$40+1\times12$ € = €

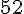
Tarif 3 : 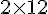$2\times12$ € = €

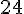
Le tarif 3 est le plus intéressant.

b. Expressions des fonctions :

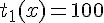
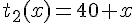
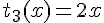
c. Représentation graphique réalisée sur le même repère orthogonal (non fournie ici).

d. Yéro va à la piscine une fois par semaine :

Nombre d’entrées par an : $1\times4\times12$ =

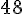
S’il y va deux fois par semaine :

Nombre d’entrées par an : $2\times4\times12$ =

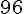
e. Tarifs les plus intéressants :

Pour 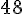entrées :

Tarif 1 : €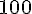

Tarif 2 : 40+48 € = €

Tarif 3 : $2\times48$ € = €

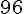
Le tarif 2 est le plus intéressant.

Pour 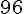entrées :

Tarif 1 : €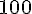

Tarif 2 : 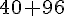40+96 € = 136 €

Tarif 3 : $2\times96$ € = 192 €

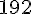
Le tarif 1 est le plus intéressant.

f. À partir de combien d’entrées l’abonnement tarif 1 devient-il intéressant ?

Nous cherchons tel que $100\leq40+x$ et $100\leq2x$ .

$x\geq60$

Exercice 8 – représentation de fonctions linéaires et affines.

Les fonctions affines données sont :

$d:x\mapsto-2x+1$
$u:x\mapsto3x-4$
$h:x\mapsto-x+3$
$t:x\mapsto2$
$k:x\mapsto2,5x$
$m:x\mapsto-2x-3$

Pour les fonctions 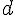et , nous remarquons qu’elles ont le même coefficient directeur, qui est .

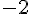
Conclusion : Les représentations graphiques des fonctions 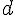et sont des droites parallèles car elles ont le même coefficient directeur. La raison est que le coefficient directeur détermine la pente de la droite, et donc les deux droites sont parallèles entre elles.

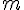
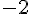
Exercice 9 – déterminer des fonctions linéaires et affines.

1. La fonction horizontale (en violet) est u(x) = 1, car elle est parallèle à l’axe des x à y = 1.

2. La fonction en jaune, passant par l’origine et croissante, a pour pente f(x) = x.

3. La fonction en bleu, décroissante, traversant l’axe des y à y = 2 et passant par (1,0), est g(x) = -2x + 2.

4. La fonction en marron, croissante, traversant l’axe des y à y = -1 et passant également par (1,0), est h(x) = x – 1.

5. Enfin, la fonction en gris, passant par (0,0) et traversant (1,-1), est k(x) = -x.

Exercice 10 – problème sur les fonctions linéaires et affines.

a. Calculer l’aire totale du CDI.

Le CDI a la forme d’un trapèze, donc l’aire se calcule en utilisant la formule de l’aire d’un trapèze :

$A=\frac{1}{2}\times (AB+DC)\times AD$

Avec AB=5 m, DC=8 m et AD=10 m, on trouve :

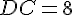
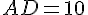
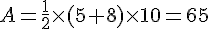
$A=\frac{1}{2}\times(5+8)\times10=65$

B. Quelles sont les valeurs possibles pour x ?

Pour que l’espace rayonnage ait un sens, il faut <img class= »LatexImg » src= »https://maths-pdf.fr/cgi-bin/mimetex.cgi?0 < x < 5″ alt= »0 < x , car 5 m est la largeur totale AB du trapèze.

c. Exprimer, en fonction de x, r(x) l’aire de l’espace rayonnage et c(x) l’aire de l’espace coin lecture en m².

L’aire de l’espace rayonnage est :

$r(x)=x\times AD=x\times 10=10x$

L’aire de l’espace coin lecture est donc :

d. Représenter, par lecture graphique, la valeur de x pour laquelle les vœux de la documentaliste seront pris en compte.

Les areas doivent être équivalentes, donc :

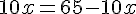
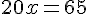
20x=65

x=3,25

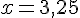
La valeur de pour laquelle les espaces ont la même aire est x=3,25 m.

4.9/5 - (36712 votes)

Télécharger puis imprimer cette fiche en PDF.

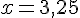
Télécharger ou imprimer cette fiche «fonctions affines : corrigé des exercices de maths en 3ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 15 340 328 cours et exercices de maths téléchargés en PDF et 4 250 exercices.