Généralités sur les fonctions : corrigé des exercices de maths en 3ème en PDF.

Mis à jour le 23 novembre 2025

Les fonctions sont un concept fondamental en mathématiques, particulièrement pour les élèves de troisième, où elles jouent un rôle crucial dans le développement de compétences analytiques. Comprendre les généralités sur les fonctions permet non seulement de résoudre des équations, mais aussi d’analyser des situations diverses en utilisant des représentations graphiques. Dans cet article, nous allons explorer les différentes compétences mathématiques travaillées liées aux fonctions et fournir des corrections d’exercices pour aider les élèves à maîtriser ce sujet essentiel.

Exercice 1 – généralité sur les fonctions

1) Par lecture graphique :

L’image de 6 par la fonction v est environ 250. En lisant le graphique, on estime que v(6) 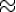$\approx$ 250 .

2) Calcul de la valeur exacte de $v(6)$ :

Utilisons la formule donnée :

$v(x)=18\pi((1+\frac{x}{6})^3-1)$

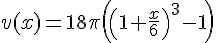
Calculons $v(6)$ :

$v(6)=18\pi((1+\frac{6}{6})^3-1)$

$=18\pi(2^3-1)$

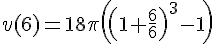
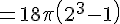
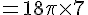
$=18\pi\times 7$

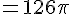
$=126\pi$

Avec ( pi 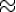$\approx$ 3,14 ), cela donne :

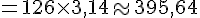
$=126\times 3,14\approx395,64$

3) Arrondir à l’unité :

L’arrondi à l’unité près de la valeur trouvée est 396 .

4) Encadrer l’antécédent de 250 :

D’après le graphique, on trouve que pour v(x) 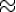$\approx$ 250 , l’antécédent est situé approximativement entre les valeurs 4 et 5.

Donc, $4 \leq\, x \leq\, 5$ .

Exercice 2 – exploitation d’une courbe – Fonctions

1) Peut-on dire que la vitesse du sportif a été constante durant toute sa course ?

Non, la vitesse n’a pas été constante. La courbe présente plusieurs paliers et des variations de pente, indiquant des changements de vitesse.

2) Le coureur s’est-il arrêté ? Si oui, pendant combien de temps ?

Oui, le coureur s’est arrêté entre 20 minutes et 22 minutes puisqu’il n’y a pas de variation de distance pendant ce temps.

3) Quelle est l’image de 5 par la fonction $d:t \mapsto d(t)$ ? Que signifie dans la pratique ce résultat ?

L’image de 5 est 30 minutes. Cela signifie que le coureur a parcouru 5 km en 30 minutes.

4) Quel est l’antécédent de 6 par la fonction $d:t \mapsto d(t)$ ? Quelle a été la durée du parcours de 6 km effectuée par le coureur ?

L’antécédent de 6 est 36 minutes. Le coureur a mis 36 minutes pour parcourir 6 km.

5) Pendant sa course, le coureur a gravi une côte.

Quand a certainement dû débuter l’ascension de cette côte ? Quelle était la longueur de cette côte ?

L’ascension de la côte a probablement débuté vers 15 minutes et s’est poursuivie jusqu’à 20 minutes. La longueur de cette côte est la différence de distances entre 15 et 20 minutes, c’est-à-dire 1 km (de 3 km à 4 km).

6) Pourquoi peut-on supposer que les 10 dernières minutes de course furent effectuées en descente ?

La pente de la courbe est plus raide pendant les 10 dernières minutes (de 26 minutes à 36 minutes), suggérant une vitesse accrue, typique d’une descente.

7) Quelle a été la vitesse moyenne de ce coureur durant les 10 dernières minutes de course ?

Quelle a été la vitesse moyenne de ce coureur sur l’ensemble de sa course ?

Vitesse moyenne des 10 dernières minutes :

Distance parcourue = 6 km – 4 km = 2 km, temps = 10 minutes = 1/6 heure. $\frac{2}{\frac{1}{6}}=12\text{ km/h}$

Vitesse moyenne sur l’ensemble de la course :

Distance totale = 6 km, temps total = 36 minutes = 0,6 heure. $\frac{6}{0,6}=10\text{ km/h}$

Exercice 3 – représentation graphique d’une courbe – Fonctions

a) L’image par h du nombre 8 :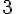

b) h(−1) :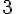

c) Les antécédents par h du nombre 0 : $x=-2\ \text{et}\ x=5$

d) L’image par h du nombre −3 :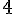

e) Les antécédents par h du nombre −2 :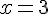

f) Les antécédents par h du nombre 2 : $x=0\ \text{et}\ x=9$

Exercice 4 – géométrie et fonctions

1.a. Construisons un triangle EFG avec les côtés suivants :

EF = 5,4 cm, EG = 7,2 cm, FG = 9 cm.

1.b. M est situé sur le segment [EF] tel que $EM=\frac{2}{3}\times EF$ . Donc :

$EM=5,4\times \frac{2}{3}=3,6$

On place M à 3,6 cm de E.

1.c. En traçant la parallèle à FG passant par M, elle coupe [EG] en N. Calculons EN comme suit :

Puisque EN est parallèle à FG dans le triangle rectangle et partage en deux le triangle, elle forme un autre triangle similaire.

1.d. EFG est un triangle rectangle en E par le théorème de Pythagore :

Donc , prouvant ainsi que le triangle est rectangle et l’aire de EMN :

$\frac{1}{2}\times EM\times EN$ .

2.a. Pour x sur [0, 5,4], M est sur [EF].

2.b. EN en fonction de x est :

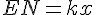
avec k = une constante trouvée par relations de proportionnalité.

2.c. Fonction A(x) est l’aire du triangle EMN :

$A(x)=\frac{1}{2}\times x \times k x = \frac{k}{2}x^2$

2.d. Lecture du graphique :

Pour A(3,5), lisez la valeur approximée sur le graphique.

Puis trouvez x tel que A(x) = 12.

Exercice 5 – problème sur les fractions.

1. Pourquoi x est compris entre 0 et 10 :

La dimension maximale du carré découpé est limitée à la moitié de la longueur du côté de la plaque, c’est-à-dire 10 cm (20 cm : 2), sans quoi les rabats ne se rencontreraient pas pour former une boîte.

2. Quelle est la hauteur de la boîte :

La hauteur de la boîte est la longueur des carrés découpés, donc cm.

3. Calculer l’aire A(x) du carré au fond de la boîte en cm² :

Le côté du carré au fond est 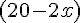cm.

Aire :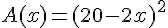

4. Calculer le volume V(x) de la boîte en cm³ :

Volume : 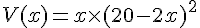$V(x)=x\times (20-2x)^2$

5. Représenter V(x) sur un graphique pour les valeurs précédentes :

Ce graphique est obtenu en traçant V(x) pour 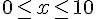$0\leq\,{x}\leq\,10$ .

6. Conjecturer la valeur x pour laquelle le volume est maximum :

En étudiant le graphique, on trouve que le volume est maximal pour 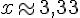$x\approx3,33$ cm.

Exercice 6 – notion de fonctions, calcul d’image et d’antécédent.

a. g(-0,1) =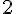

b. g(…) = 1

Réponse :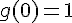

c. g(…) = -4

Réponse :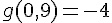

d. g(0,7) =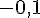

Exercice 7 – lecture d’image et d’antécédent à partir d’un graphique.

a. Quelle est l’image de 0 par la fonction h ?

L’image de 0 par la fonction h est .

b. Quels nombres ont pour image 0 par la fonction h ?

Les nombres qui ont pour image 0 sont 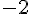et .

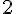
c. Donner une valeur approchée de :

– L’image de 4 par la fonction h.

Une valeur approchée de l’image de 4 par la fonction h est .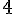

– L’image de -3 par la fonction h.

Une valeur approchée de l’image de -3 par la fonction h est .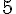

Exercice 8 – tableau de valeurs et nombre d’antécédents.

a. 3,5

L’antécédent de 3,5 est x = 0.

b. -2

Les antécédents de -2 sont x = -1,5 et x = 2.

c. 2

Il n’y a aucun antécédent pour 2 dans ce tableau.

Exercice 10 – hauteur d’un triangle équilatéral et fonctions.

a. Calculons la hauteur et l’aire d’un triangle équilatéral de côté 5 cm.

– La hauteur d’un triangle équilatéral de côté c est donnée par la formule : $h=\frac{\sqrt{3}}{2}\times c$ .

– Pour c = 5 cm, la hauteur est : $h=\frac{\sqrt{3}}{2}\times 5=\frac{5\sqrt{3}}{2}$

– L’aire A du triangle est : $A=\frac{1}{2}\times base\times hauteur=\frac{1}{2}\times 5\times \frac{5\sqrt{3}}{2}=\frac{25\sqrt{3}}{4}$

b. Exprimer la hauteur en fonction de 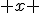$ x $.

– La hauteur h en fonction de x est : $h(x)=\frac{\sqrt{3}}{2}\times x$

c. Déterminer une expression de la fonction f et calculer f(5) , f(3), et 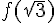$f(\sqrt{3})$ .

– La fonction f(x) qui associe à x l’aire du triangle équilatéral est : $f(x)=\frac{\sqrt{3}}{4}\times x^2$

– Calcul de f(5) : 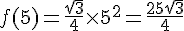$f(5)=\frac{\sqrt{3}}{4}\times 5^2=\frac{25\sqrt{3}}{4}$

– Calcul de f(3) : 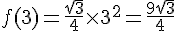$f(3)=\frac{\sqrt{3}}{4}\times 3^2=\frac{9\sqrt{3}}{4}$

– Calcul de 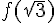$f(\sqrt{3})$ : $f(\sqrt{3})=\frac{\sqrt{3}}{4}\times (\sqrt{3})^2=\frac{3\sqrt{3}}{4}$

4.8/5 - (36623 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «généralités sur les fonctions : corrigé des exercices de maths en 3ème en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Homothéties

Sections de solides et volumes

Arithmétique et décomposition en facteurs premiers

Coordonnées géographiques

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 387 148 cours et exercices de maths téléchargés en PDF et 4 250 exercices.