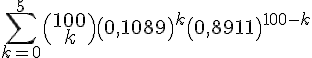Probabilités conditionnelles : corrigé des exercices de maths en terminale en PDF

Mis à jour le 23 novembre 2025

Dans le cadre de leur parcours en maths en terminale, les élèves doivent maîtriser les probabilités conditionnelles, un concept clé pour la compréhension des enjeux statistiques. Ce sujet est crucial non seulement pour réussir l’enseignement supérieur, mais également pour développer des compétences analytiques et logiques indispensables. En corrigant des exercices de probabilités, les étudiants affinent leur résolution de problèmes et leur capacité à interpréter des données complexes, renforçant ainsi leur savoir-faire en statistiques.

Exercice 1 – probabilité et étude de boules dans une urne.

Soit le nombre initial de boules rouges et le nombre initial de boules bleues.

1. Première situation : La première boule tirée est rouge :

Après le remplacement et le doublement, les boules deviennent : rouges et bleues.

La probabilité de tirer une boule rouge au deuxième tir est :

$\frac{2n}{2n+p}=\frac{16}{33}$

On résout alors :

$\frac{2n}{2n+p}=\frac{16}{33}$

Résolvons : $33\times 2n=16\times (2n+p)$

$\frac{n}{p}=\frac{8}{17}$

2. Deuxième situation : La première boule tirée est bleue :

Après le remplacement et le doublement, les boules deviennent : rouges et bleues.

La probabilité de tirer une boule bleue au deuxième tir est :

$\frac{2p}{n+2p}=\frac{17}{21}$

On résout alors :

$21\times 2p=17\times (n+2p)$

$\frac{p}{n}=\frac{17}{8}$

Conclusion : À partir des équations $\frac{n}{p}=\frac{8}{17}$ et $\frac{p}{n}=\frac{17}{8}$ , nous validons les proportions et vérifions l’exactitude.

Valeurs possibles : et où est un nombre entier positif.

Exercice 2 – probabilités et test danss une entreprise.

a) Traduire les informations en probabilités :

– La probabilité qu’un candidat soit un garçon est .

– La probabilité qu’un candidat soit une fille est .

– La probabilité qu’un garçon soit engagé est $P(E\mid G)=0,7$ .

– La probabilité qu’une fille soit engagée est $P(E\mid F)=0,8$ .

b) Représentation par un arbre pondéré :

1. Niveau 1 :

Garçon, probabilité :
Fille, probabilité :

2. Niveau 2 :

Garçon engagé, probabilité conditionnelle :
Garçon non engagé, probabilité :
Fille engagée, probabilité conditionnelle :
Fille non engagée, probabilité :

c) Calcul de la probabilité qu’une candidate soit une fille et soit engagée :

Il s’agit de calculer $P(F\cap E)$ :

$P(F\cap E)=P(F)\times P(E\mid F)=0,4\times 0,8$

Donc, $P(F\cap E)=0,32$ .

Exercice 3 – sondage auprès des vacanciers et arbre pondéré.

a) Arbre pondéré :

Commençons par représenter la situation avec un arbre pondéré :

                      S : 0,45
                     /       \
              N : 0,60     N : 0,40
                /           \
             0,27         0,18
                (Natation) (Pas de natation)

                    S^c : 0,55
                   /       \
             N : 0,70     N : 0,30
               /           \
            0,385        0,165
               (Natation) (Pas de natation)

b) Calcul de la probabilité que le vacancier ne fréquente pas de salle de sport et ne pratique pas la natation :

On utilise la branche correspondant à ne fréquente pas de salle de sport et ne pratique pas la natation.

La probabilité est : $P(S^c\cap\overline{N})=0,55\times 0,30=0,165$

Exercice 4 – une étude de dragées dans une boîte.

1) Recopier et compléter l’arbre pondéré :

Probabilités initiales :
Amande :
Sans amande : $P(\overline{A})=0,7$

Pour les dragées avec amande :
Bleue :
Rose : $P(\overline{B}|A)=0,6$

Pour les dragées sans amande :
Bleue : $P(B|\overline{A})=0,75$
Rose : $P(\overline{B}|\overline{A})=0,25$

2) Montrer que $P(A\cap B)=0,12$

$P(A\cap B)=P(A)\times P(B|A)=0,3\times 0,4=0,12$

3) Calculer

$P(B)=P(A\cap B)+P(\overline{A}\cap B)$

$P(\overline{A}\cap B)=P(\overline{A})\times P(B|\overline{A})=0,7\times 0,75=0,525$

Donc

4) En déduire

$P_B(A)=\frac{P(A\cap B)}{P(B)}=\frac{0,12}{0,645}\approx0,186$

5) Calculer $P_{\overline{B}}(A)$

$P(\overline{B})=1-0,645=0,355$

Pour $P_{\overline{B}}(A)$

$P(A\cap\overline{B})=P(A)\times P(\overline{B}|A)=0,3\times 0,6=0,18$

$P_{\overline{B}}(A)=\frac{P(A\cap\overline{B})}{P(\overline{B})}=\frac{0,18}{0,355}\approx0,507$

6) Sophie préfère les dragées contenant une amande. Doit-elle plutôt choisir une dragée bleue ou bien une dragée rose ?

Sophie a plus de chances de choisir une dragée contenant une amande parmi les dragées roses, car $P_{\overline{B}}(A)\approx0,507$ est supérieur à $P_B(A)\approx0,186$ .

Exercice 5 – une épidémie dans un pays et les probabilités.

1) Représentation par un arbre pondéré

On peut représenter la situation par un arbre de probabilités :

Un individu non touché par la maladie : 90%

Test positif : 1% de 90% soit $0,01\times 0,90$ = 0,009
Test négatif : 99% de 90% soit $0,99\times 0,90$ = 0,891

Un individu touché par la maladie : 10%

Test positif : 0,1% de 10% soit $0,999\times 0,10$ = 0,0999
Test négatif : 0,1% de 10% soit $0,001\times 0,10$ = 0,0001

2a) Montrer que le traitement est donné à 10,89 % de la population

La probabilité qu’un individu ait un test positif est :

Donc, 10,89% de la population.

2b) Pourcentage de la population recevant le traitement à tort

Le traitement est donné à tort aux individus non malades ayant un test positif :

$0,009\times 100=0,9\%$

3a) Probabilité que 10 individus soient sous traitement

On utilise la loi binomiale : .

La probabilité est donnée par la formule de la loi binomiale :

$P(X=10)=\binom\,{100}{10}(0,1089)^{10}(0,8911)^{90}$

3b) Probabilité que 5 individus ou moins soient sous traitement

Il faut calculer : $P(X\leq\,5)$

Cela se fait en calculant la somme des probabilités individuelles de 0 à 5 :

$\sum_{k=0}^{5}\binom\,{100}{k}(0,1089)^{k}(0,8911)^{100-k}$

Exercice 6 – compléter des arbres de probabilité.

Pour compléter l’arbre 2 à l’aide de l’arbre 1, nous devons examiner les probabilités de l’arbre 1 et les transposer dans l’arbre 2.

Première branche:

Dans l’arbre 1, la probabilité d’avoir $A$ est $\frac{1}{5}$ . La branche correspondante dans l’arbre 2 sera :

Pour $B$ après $A$, la probabilité est $\frac{1}{8}$ . Donc pour $A$, la branche sera $\frac{1}{5}\times \frac{1}{8}=\frac{1}{40}$ .
Pour $\,\overline{B}$ après $A$, la probabilité est $\frac{7}{8}$ . Donc pour $\,\overline{A}$, la branche sera $\frac{1}{5}\times \frac{7}{8}=\frac{7}{40}$ .

Deuxième branche:

Pour $\,\overline{A}$, la probabilité est $\frac{4}{5}$ :

Pour $B$ après $\,\overline{A}$, la probabilité est $\frac{4}{9}$ . Donc pour $A$, la branche sera $\frac{4}{5}\times \frac{4}{9}=\frac{16}{45}$ .
Pour $\,\overline{B}$ après $\,\overline{A}$, la probabilité est $\frac{5}{9}$ . Donc pour $\,\overline{A}$, la branche sera $\frac{4}{5}\times \frac{5}{9}=\frac{20}{45}=\frac{4}{9}$ .

En résumé, l’arbre 2 est complété comme suit :

$(A, B)$ avec une probabilité de $\frac{1}{40}$ .
$(A, \,\overline{B})$ avec une probabilité de $\frac{7}{40}$ .
$(\,\overline{A}, B)$ avec une probabilité de $\frac{16}{45}$ .
$(\,\overline{A}, \,\overline{B})$ avec une probabilité de $\frac{4}{9}$ .

Exercice 7 – une tombola et l’expérience aléatoire.

1) Calcul de la probabilité pour le deuxième lot :

Pour calculer la probabilité $ x $ d’obtenir le lot de 2 €, on doit d’abord calculer le coût attendu par ticket. On veut que ce coût soit de 1,71 €.

Calculons d’abord le coût moyen d’un ticket gagnant :

– 80 % de chance d’obtenir 1 € : $0,8\times 1$

– $ x $ % de chance d’obtenir 2 € : $\frac{x}{100}\times 2$

– $ (20-x) $ % de chance d’obtenir 100 € : $\frac{20-x}{100}\times 100$

Le coût moyen pour un ticket gagnant est donc :

$0,8\times 1+\frac{x}{100}\times 2+\frac{20-x}{100}\times 100$

On a 20 % de tickets gagnants, donc :

$0,2\times (0,8+\frac{x}{50}+\frac{2000-100x}{100})=1,71$

En résolvant cette équation, on trouve $ x \approx 15,5 $ %.

2) Expérience aléatoire proposée :

Pour réaliser ce tirage au sort, on peut utiliser un générateur de nombres aléatoires :

Générer un nombre entre 1 et 100 :

Si le nombre est entre 1 et 80, lot de 1 €.
Si le nombre est entre 81 et 95, lot de 2 €.
Si le nombre est entre 96 et 100, lot de 100 €.

Exercice 8 – achat de pain et événement.

1) Calculer $ p_2 $ et $ p_3 $.

La probabilité que Bill achète du pain le 2ème jour, sachant qu’il en a acheté le 1er jour, est donnée par :

Pour le 3ème jour, la probabilité que Bill achète du pain est :

$p_3=0,8\times 0,3+0,3\times 0,3=0,39$

2) Représenter la situation par un arbre.

Voici un arbre montrant les événements :

– Jour 1 : $ P(A_1) = 1 $

– Jour 2 : Si $ A_1 $, alors $ P(A_2|A_1) = 0,3 $, sinon $ P(A_2|\overline{A_1}) = 0,8 $

– Jour 3 : Combinaison $ P(A_3|A_2) $ et $ P(A_3|\overline{A_2}) $

3) Montrer que $ p_{n+1} = 0,8 – 0,5 p_n $.

Nous avons :

$p_{n+1}=(0,8\times (1-p_n))+0,3p_n$

Calcul : $p_{n+1}=0,8-0,5p_n$

4) Montrer que $ p_n = \frac{7}{15}(1-(\frac{1}{2})^{n-1})+\frac{8}{15} $ pour tout $ n \in \mathbb{N}^* $.

Nous avons une suite géométrique où :

– La solution de l’équation est obtenue en résolvant l’équation récurrente.

– La forme générale est en fonction de n.

5) a) En déduire $\lim_{n \to +\infty} p_n$.

En posant la limite lorsque $ n \to +\infty $, nous trouvons :

$\lim_{n\to+\infty}p_n=\frac{8}{15}$

b) Interpréter concrètement le résultat de la question précédente.

Le résultat montre que, à long terme, la probabilité que Bill achète du pain tend vers $\frac{8}{15}$, ce qui signifie qu’il achètera du pain environ 53% du temps.

Exercice 9 – deux événements indépendants.

a) Pour les événements indépendants $A$ et $B$, nous savons que :

$P(A \cap B) = P(A) \times P(B)$

En remplaçant les valeurs, nous avons :

$0,085 = 0,15 \times P(B)$

Donc, $P(B) = \frac{0,085}{0,15}$

$P(B)=\frac{0,085}{0,15}\approx0,567$

b) Pour les événements indépendants $E$ et $F$, nous avons :

$P(E \cap F) = P(E) \times P(F)$

Avec $P(F) = 1 – P(\overline{F}) = 1 – 0,53 = 0,47$

En remplaçant les valeurs, nous avons :

$0,25 = P(E) \times 0,47$

Donc, $P(E) = \frac{0,25}{0,47}$

$P(E)=\frac{0,25}{0,47}\approx0,532$

c) Pour les événements indépendants $C$ et $D$, nous avons :

La formule pour l’union $P(C \cup D) = P(C) + P(D) – P(C \cap D)$

Comme $C$ et $D$ sont indépendants, $P(C \cap D) = P(C) \times P(D)$.

En remplaçant les valeurs, nous avons :

$0,23 = 0,11 + P(D) – (0,11 \times P(D))$

Donc, $P(D) = \frac{0,23 – 0,11}{0,89}$

$P(D)=\frac{0,12}{0,89}\approx0,135$

Exercice 10 – don de sang et probabilité sur les autorisations.

Calculons la probabilité que Ben soit là quand Nat’ rentrera.

On note :

L’événement A : « Nat’ n’est pas autorisée à donner son sang »
L’événement B : « Ben choisit d’aller faire du vélo »

On sait que :

La probabilité que Nat’ ne soit pas autorisée à donner son sang est $\frac{1}{5}$
La probabilité que Ben aille faire du vélo est

Puisque les événements sont indépendants, la probabilité que Nat’ ne soit pas autorisée et que Ben aille faire du vélo est :

$P(A\cap B)=P(A)\times P(B)=\frac{1}{5}\times 0,85$

Calculons cette probabilité :

$\frac{1}{5}\times 0,85=0,17$

La probabilité que Ben soit là quand Nat’ rentrera est donc :

La probabilité que Ben soit là quand Nat’ rentrera est

4.9/5 - (33981 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «probabilités conditionnelles : corrigé des exercices de maths en terminale en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Logarithme népérien

Produit scalaire de l’espace

Raisonnement par récurrence

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 344 318 cours et exercices de maths téléchargés en PDF et 4 250 exercices.