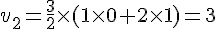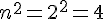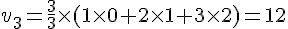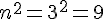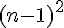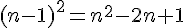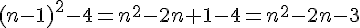Limites de suites : corrigé des exercices de maths en terminale en PDF
Mis à jour le 25 novembre 2025
Exercice 1 – tableur et conjecture de l’expression de la suite en fonction de n.
a) Pour comparer 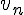
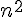

On observe que 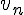
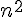

b) Conjecturons une expression de 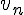

Calculons le terme général :
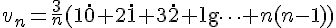
En utilisant la somme des entiers de 1 à 
Ce qui simplifie à :
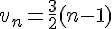
c) En admettant cette conjecture, déterminons la limite de la suite 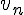
La limite de 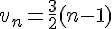
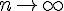

Exercice 2 – donner la limite de chaque suite.
a) Pour tout 


La limite est 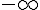
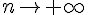

b) Pour tout 


La limite est 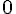

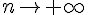
c) Pour tout 

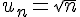
La limite est 

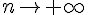
d) Pour tout 

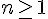

La limite est 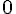

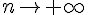
Exercice 3 – dire si la suite définie a pour limite l’infini.
a) 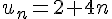
La suite 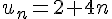
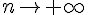
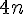
b) 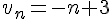
La suite 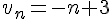
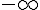
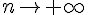
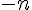
c) 
La suite 
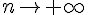
d) 
La suite 
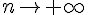
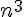
Exercice 4 – tableur et conjecture de la limite.
1. Suite 
On observe que les valeurs de 
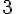

Il n’y a pas de limite, car la suite tend vers l’infini.
2. Suite 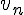
Les termes de 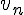
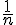
En augmentant 
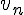
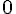
3. Suite 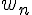
Les termes de 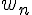
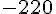
Ainsi, on conjecture que la limite est :
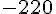
4. Suite 
Les termes de 

La limite de cette suite est :
Exercice 5 – calculatrice et limite de chacune des suites.
a) Tabuler les premiers termes de chaque suite u et v :
Pour 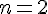

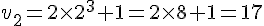
Pour 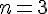
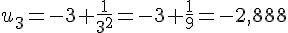
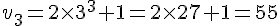
Pour 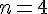
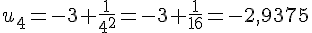
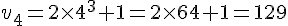
b) Conjecturer la limite de chacune des suites.
La suite 
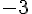
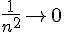
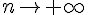
La suite 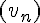

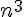
c) À partir de quel rang a-t-on :
![u_n\in]-3,01;-2,99[](https://maths-pdf.fr/latex-images/0b149e99f4390d083150b4e2340282e0.png)
Il faut 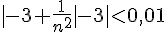

Comme 



![v_n\in]10^4;+\infty[](https://maths-pdf.fr/latex-images/ea17c8859eac64a6edf5f357dab38602.png)
Il faut 
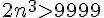

En prenant la racine cubique, on trouve 

Exercice 6 – algorithme et suites numériques.
a) Expliquer son rôle. Cet algorithme permet de déterminer le plus petit entier 
tel que la suite 
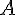
Il initialise 
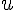


b) Coder l’algorithme dans un langage de programmation.
python
def trouve_n(A):
n = 0
u = 2
while u <= A:
n += 1
u = (3 * n + 4) ** 0.5
return n
# Exemple de test
print(trouve_n(50))
print(trouve_n(100))
print(trouve_n(500))
c) Exécuter le programme. En exécutant le programme :
- Pour
- Pour
- Pour
d) Conjecturer la limite de la suite 
La suite 

Démontrer cette conjecture.
Pour démontrer que la suite 
on remarque que :

Le terme dominant dans l’expression sous la racine est 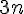
e qui implique que 
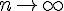
Exercice 7 – démontrer que la suite converge.
Pour montrer que la suite 
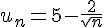
nous devons prouver que pour tout 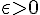
il existe un entier naturel 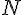

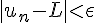
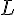
Observons que:
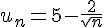
Lorsque 
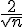

On doit donc montrer que pour tout 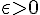
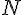


Calculons l’écart :

Nous voulons que : 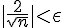
Ainsi, pour 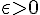



Conclusion : La suite 
Exercice 8 – démontrer que la suite a pour limite l’infini.
1. Conjecturer la limite de la suite :
Avec la calculatrice, en observant les premiers termes de la suite définie par 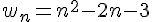


2a. Vérification de l’expression :
Vérifions que pour tout 
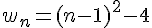
- Développement de
- Donc
- Les expressions sont équivalentes, donc la vérification est correcte.
2b. Démonstration que la suite a pour limite +∞ :
Pour montrer que la suite 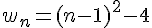

- Les termes
- En ajoutant
- Donc quand
Exercice 9 – convergence d’une suite et étude.
1. Étude de la suite 
a) Démontrer que, pour tout 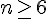

La suite 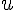
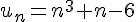
Nous devons montrer que : 
En simplifiant, cela revient à : 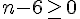
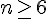
b) En déduire la limite de la suite 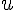
Pour 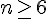


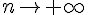
Donc, par le théorème de comparaison, la limite de 

2. Étude de la convergence de la suite 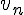
La suite 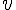

Pour étudier la convergence de 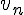

Ainsi, 
Or, la série 
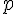
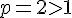

Donc, la suite 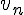
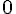
Exercice 10 – suite et preuve par récurrence.
a) Démontrer que, pour tout 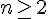

Pour démontrer cette inégalité, on commence par écrire :
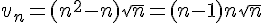
Pour que 

En simplifiant par 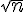
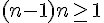
Pour 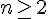
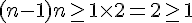
Donc, pour tout 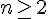

b) En déduire la limite de la suite 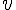
Pour trouver la limite de la suite 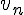
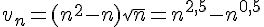
Lorsque 


Donc, la limite de 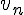

Télécharger ou imprimer cette fiche «limites de suites : corrigé des exercices de maths en terminale en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.