Intervalles de fluctuation : corrigé des exercices de maths en terminale en PDF
Mis à jour le 25 novembre 2025
Exercice 1 – des fusées pour un feu d’artifice.
1) Quelle loi suit X ? Préciser ses paramètres.
La variable aléatoire 


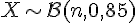
2) Déterminer l’intervalle de fluctuation asymptotique de la fréquence de fusées opérationnelles au seuil de 95% en fonction de 
L’intervalle de fluctuation asymptotique au seuil de 95% pour la fréquence est donné par :
3) En déduire l’intervalle de fluctuation asymptotique du nombre de fusées opérationnelles au seuil de 95% en fonction de 
Multipliant l’intervalle précédent par 
4) Déterminer la quantité de fusées que Samuel doit acheter pour être sûr au seuil de 95% d’avoir au moins 100 fusées opérationnelles.
Pour garantir avec 95% de confiance qu’il y ait au moins 100 fusées opérationnelles, il faut que le bord inférieur de l’intervalle de fluctuation asymptotique du nombre de fusées soit au moins 100 :
En résolvant cette inéquation, Samuel doit acheter environ 123 fusées.
Exercice 2 – intervalle de fluctuation et équilibre d’un dé.
1) 200 fois le nombre 1 :
La fréquence obtenue est 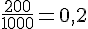
Cette fréquence n’appartient pas à l’intervalle [0,143 ; 0,190].
Conclusion : Le dé n’est probablement pas équilibré.
2) 150 fois le nombre 1 :
La fréquence obtenue est 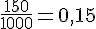
Cette fréquence appartient à l’intervalle [0,143 ; 0,190].
Conclusion : Il est probable que le dé soit équilibré.
Exercice 3 – l’intervalle contenant p avec une probabilité.
On sait que l’intervalle suivant contient la fréquence 
![[p-\frac{1}{\sqrt{n}};p+\frac{1}{\sqrt{n}}]](https://maths-pdf.fr/latex-images/24f607f64041809264a7b547303f0f65.png)
On nous demande de prouver que l’intervalle suivant contient 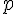
![[f-\frac{1}{\sqrt{n}};f+\frac{1}{\sqrt{n}}]](https://maths-pdf.fr/latex-images/cef87d9f18b00fee8ca5ce3bcd1de424.png)
Si la fréquence 
![f\in[p-\frac{1}{\sqrt{n}};p+\frac{1}{\sqrt{n}}]](https://maths-pdf.fr/latex-images/a8968a9d52070a269fda1ecb9711cd9d.png)
Alors, cela implique directement que 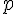
![p\in[f-\frac{1}{\sqrt{n}};f+\frac{1}{\sqrt{n}}]](https://maths-pdf.fr/latex-images/1c7dd732e9fc8abbdd77d1cede52bf87.png)
Ceci découle directement du fait que les intervalles sont centrés sur les valeurs réciproques. Ainsi, l’intervalle ![[f-\frac{1}{\sqrt{n}};f+\frac{1}{\sqrt{n}}]](https://maths-pdf.fr/latex-images/cef87d9f18b00fee8ca5ce3bcd1de424.png)
Exercice 4 – algorithme et probabilités.
1) Compléter les lignes 11 et 13 de l’algorithme.
Ligne 11 : Afficher « On peut rejeter cette hypothèse au seuil de » f
Ligne 13 : Afficher « On ne peut pas rejeter cette hypothèse au seuil de » f
2) Que fait-il ?
Cet algorithme détermine si l’on peut ou non rejeter une hypothèse statistique basée sur une proportion 


3) Modifier l’algorithme pour qu’il demande d’abord à l’utilisateur s’il souhaite un seuil de 95% ou de 99%.
4. Traitement et affichage modifié
5. Demander à l’utilisateur de choisir le seuil (95% ou 99%)
6. Si seuil choisi = 95% Alors
7. Donner 
8. Sinon
9. Donner 
10. Fin Si
11. Demander 
12. Demander 
13. Demander 
14. Donner à 

15. Donner à 

16. (suite identique)
Exercice 5 – une compagnie ferroviaire et fluctuation.
1) Déterminer l’intervalle de fluctuation :
Le pourcentage de trains arrivant à l’heure annoncé est de 90% soit 0,9. On utilise la formule de l’intervalle de fluctuation pour une proportion, qui est :
où p = 0,9 et n = 60.
Calculons :
Intervalle :
2) Cet usager a relevé que son train avait eu 12 fois du retard.
a) Déterminer la fréquence des trains arrivés à l’heure :
Le nombre de jours où le train est arrivé à l’heure est 60 – 12 = 48.
La fréquence est donc :

0,8 n’appartient pas à l’intervalle [0,8242 ; 0,9758].
b) Proposer deux hypothèses :
- Hypothèse 1 : Il se peut que la compagnie ait surévalué le pourcentage de trains arrivant à l’heure.
- Hypothèse 2 : Les conditions de circulation peuvent être moins favorables sur la ligne que cet usager emprunte.
Exercice 6 – une étude de l’INSEE sur les bébés français hors mariage.
1) Déterminer l’intervalle de fluctuation asymptotique au seuil de 95 % :
On considère que la proportion de naissances hors mariage en 2006 est de 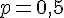

L’intervalle de fluctuation asymptotique à 95 % pour une proportion se calcule avec la formule :
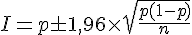
En remplaçant par les valeurs données :
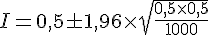
Calculons l’écart-type : 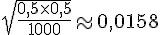
L’intervalle devient :
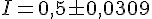
Soit un intervalle de :
![[0,4691;0,5309]](https://maths-pdf.fr/latex-images/8beccadb827347073e71417a68c5d6a3.png)
2) Que peut-on en déduire concernant l’hypothèse émise ?
La proportion observée en 2010 est 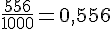
Puisque 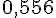
![[0,4691;0,5309]](https://maths-pdf.fr/latex-images/8beccadb827347073e71417a68c5d6a3.png)
Exercice 7 – un producteur de jus de pomme et sa commercialisation.
1) Loi suivie par X :
Sous l’hypothèse que la proportion n’a pas changé, X suit une loi binomiale de paramètres 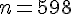
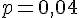
2) Intervalle de fluctuation asymptotique à 95% :
On utilise l’approximation normale car 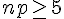
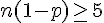
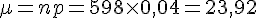
et l’écart-type est
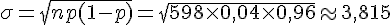
L’intervalle de fluctuation à 95% est :
![[np-1,96\sigma;np+1,96\sigma]](https://maths-pdf.fr/latex-images/8c5527f03f55eb33f279fc06846695df.png)
qui donne environ :
![[23,92-1,96\times3,815;23,92+1,96\times3,815]](https://maths-pdf.fr/latex-images/465bf169f27226dfff4bc6f82875aaa9.png)
soit :
![[16,49;31,35]](https://maths-pdf.fr/latex-images/7ddff5dc21111cf9da06ac6cdc682c21.png)
3) Conclusion :
Le producteur a trouvé 19 bouteilles non commercialisables. Ce nombre est dans l’intervalle de fluctuation [16,49;31,35]. Il ne peut donc pas affirmer avec une confiance de 95% qu’il a fait mieux que l’année dernière.
Exercice 8 – déterminer l’intervalle de fluctuation asymptotique.
Réponse 1 : Pour 
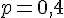
L’intervalle est donné par :
En calculant :
Résultat final :
Réponse 2 : Pour 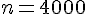
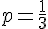
L’intervalle est donné par :
Résultat final :
Réponse 3 : Pour 
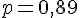
L’intervalle est donné par :
Résultat final :
Exercice 9 – la population française et le port de lunettes.
1) Quelle loi suit X ?
X suit une loi binomiale de paramètres 


2) Vérification des conditions :
Vérifions les conditions :
:
:
:
Les conditions sont bien vérifiées.
3) Intervalle de fluctuation au seuil de 95 % :
Utilisons l’approximation normale pour calculer l’intervalle :
La moyenne : 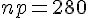
La variance : 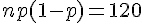
Écart-type : 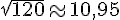
L’intervalle de fluctuation asymptotique à 95 % est donné par :
![[np-1,96\times\sigma\,;\,np+1,96\times\sigma]](https://maths-pdf.fr/latex-images/920967d121015054d2254a6898e8f3c3.png)
Calculons :
![[280-1,96\times10,95\,;\,280+1,96\times10,95]](https://maths-pdf.fr/latex-images/9295ac3b0d946920667176b5819ce8c0.png)
![[258,54\,;\,301,46]](https://maths-pdf.fr/latex-images/63959668acb983da9c5432e16037ebc8.png)
4) Interprétation :
Concrètement, cela signifie que, si l’on répète plusieurs tirages d’échantillons de 400 personnes, dans 95 % des cas, le nombre de personnes portant des lunettes ou des lentilles sera compris entre 259 et 301.
Exercice 10 – lancers d’une pièce équilibrée.
1) a) Intervalle de fluctuation asymptotique de la fréquence de « pile » au seuil de 95%
Pour un seuil de confiance de 95%, on utilise une valeur critique de 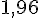
La fréquence théorique de « pile » est 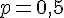
L’intervalle est donné par :
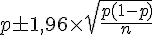
Donc :
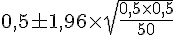
Calculons :
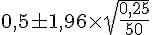
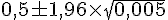
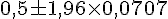
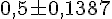
Ce qui donne l’intervalle :
b) Intervalle de fluctuation asymptotique de X au seuil de 95%
On multiplie l’intervalle précédent par 
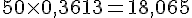
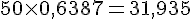
Ce qui arrondi donne l’intervalle pour X :
2) Intervalle de fluctuation asymptotique de X au seuil de 99%
Pour un seuil de confiance de 99%, on utilise une valeur critique de 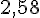

Donc :
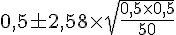
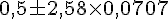
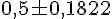
L’intervalle des fréquences est :
Pour X, cela donne :
Soit :
Avec des valeurs arrondies, on obtient :
Télécharger ou imprimer cette fiche «intervalles de fluctuation : corrigé des exercices de maths en terminale en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.

![[0,85 -1,96\times \sqrt{\frac{0,85\times 0,15}{n}},0,85 +1,96\times \sqrt{\frac{0,85\times 0,15}{n}}]](https://maths-pdf.fr/latex-images/2399e44c432df1ed6e96c7a64ea00e81.png)
![n\times [0,85 -1,96\times \sqrt{\frac{0,85\times 0,15}{n}},0,85 +1,96\times \sqrt{\frac{0,85\times 0,15}{n}}]](https://maths-pdf.fr/latex-images/b787dd3e6babbfd4c3fdb862aa324e89.png)

![]p-1,96\times \sqrt{\frac{p(1-p)}{n}} \; ; \; p+1,96\times \sqrt{\frac{p(1-p)}{n}}[](https://maths-pdf.fr/latex-images/1dd6434401d98741fffec15f9f68867a.png)




![[0,8242 \; ; \; 0,9758]](https://maths-pdf.fr/latex-images/5ffa38b3af6708c5970b0643fe13bbd3.png)
![[p-1,96\times \sqrt{\frac{p(1-p)}{n}}; p+1,96\times \sqrt{\frac{p(1-p)}{n}}]](https://maths-pdf.fr/latex-images/9422bf6df19ca8b9ebc2248753482979.png)
![[0,4-1,96\times \sqrt{\frac{0,4\times 0,6}{100}}; 0,4+1,96\times \sqrt{\frac{0,4\times 0,6}{100}}]](https://maths-pdf.fr/latex-images/a31e4327e9c5d574a8fb536b56ad6eb9.png)
![[0,32; 0,48]](https://maths-pdf.fr/latex-images/8219704d0107c0af4682ccfb4d29de12.png)
![[\frac{1}{3}-1,96\times \sqrt{\frac{\frac{1}{3}\times \frac{2}{3}}{4000}}; \frac{1}{3}+1,96\times \sqrt{\frac{\frac{1}{3}\times \frac{2}{3}}{4000}}]](https://maths-pdf.fr/latex-images/448c3e4ec1107797eb3962fd34362d21.png)
![[0,31; 0,36]](https://maths-pdf.fr/latex-images/b85080e4ac52c50f823f1b2f38c4e69c.png)
![[0,89-2,576\times \sqrt{\frac{0,89\times 0,11}{77}}; 0,89+2,576\times \sqrt{\frac{0,89\times 0,11}{77}}]](https://maths-pdf.fr/latex-images/0f651ff28eb520f97a853053b20e1f76.png)
![[0,83; 0,95]](https://maths-pdf.fr/latex-images/12bafe57b07948c713f2854c32fa2891.png)
 :
: 
 :
: 
 :
: 
![[0,3613\ ;\ 0,6387]](https://maths-pdf.fr/latex-images/1d7d5830037d5ed6c9350c81d32a6fcf.png)
![[18\ ;\ 32]](https://maths-pdf.fr/latex-images/0cfbdca1e64ff1c21eaef95e50ac641e.png)
![[0,3178\ ;\ 0,6822]](https://maths-pdf.fr/latex-images/1c27872b795d9c59a516eeef0cc686d7.png)
![[50\times 0,3178\ ;\ 50\times 0,6822]](https://maths-pdf.fr/latex-images/af83e8839093495b55c505e5fe5d82e6.png)
![[15,89\ ;\ 34,11]](https://maths-pdf.fr/latex-images/6b9b4c16237ae84cd8ccf317308895a7.png)
![[16\ ;\ 34]](https://maths-pdf.fr/latex-images/79c9d83a9fc5074920228bdc1eb17517.png)




