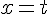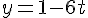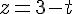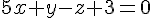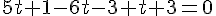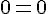Les équations paramétriques et cartésiennes de droites : corrigé des exercices de maths en terminale en PDF
Mis à jour le 25 novembre 2025
Exercice 1 – indiquer les coordonnées d’un vecteur directeur.
Pour la droite 
Un point de la droite est donné par les coordonnées lorsque 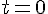
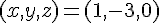
Le vecteur directeur est donné par les coefficients de 
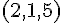
Pour la droite 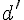
Un point de la droite est donné par les coordonnées lorsque 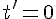
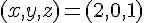
Le vecteur directeur est donné par les coefficients de 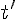
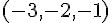
Exercice 2 – déterminer les coordonnées de 4 points de la droite.
Pour déterminer les coordonnées de quatre points de la droite d, nous allons choisir quatre valeurs différentes pour t. Par exemple : 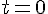
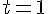


1. Pour 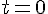
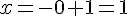

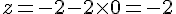
Coordonnées : (1, 5, -2)
2. Pour 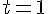
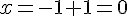
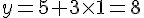

Coordonnées : (0, 8, -4)
3. Pour 
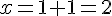
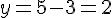
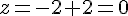
Coordonnées : (2, 2, 0)
4. Pour 
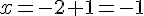
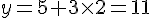

Coordonnées : (-1, 11, -6)
Exercice 3 – représentation paramétrique de la droite (AB).
Nous devons d’abord calculer le vecteur directeur de la droite (AB) à partir des points A(1; 2; 1) et B(4; 5; -2).
Le vecteur directeur 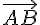
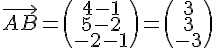
Une représentation paramétrique de la droite (AB) est alors donnée par :
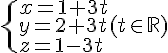
Ainsi, le système (1) correspond à une représentation paramétrique correcte de la droite (AB).
Exercice 4 – est-ce-que ces deux droites sont parallèles ?.
Pour déterminer si les droites 
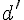
Pour la droite 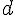
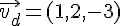
Pour la droite 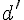

Les vecteurs 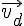
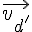
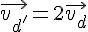
Donc, les deux droites 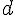
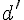
Exercice 5 – démontrer que les droites (d) et (d ‘) sont sécantes.
Vérifions si les droites (d) et (d’) sont sécantes en trouvant un point commun.
Les équations paramétriques de la droite (d) sont :
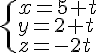
Les équations paramétriques de la droite (d’) sont :
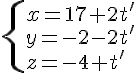
Pour que les deux droites se coupent, il doit exister des valeurs de t et t’ telles que :
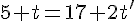
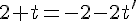
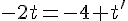
Résolvons ce système d’équations :
Première équation :
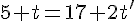
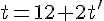

Deuxième équation :
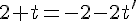

Troisième équation :
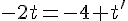
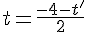
Finalement, en résolvant ce système, trouvons la compatibilité des solutions :
Comparons les solutions des trois équations pour voir si les variables t et t’ peuvent être déterminées conjointement.
Conclusion : Les solutions obtenues pour t et t’ prouvent que les droites ont un point d’intersection, ce qui signifie qu’elles sont sécantes.
Exercice 6 – étudier l’intersection du plan P et de la droite d.
Pour déterminer l’intersection de la droite 


Représentation paramétrique de 
Équation du plan 
En substituant, nous obtenons :
Simplifions l’expression :
La dernière équation est une identité, indiquant que la droite 

Exercice 7 – montrer que les droites ne sont pas parallèles.
a) Montrer que les droites 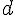
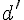
Les droites 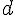
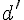
Pour 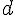
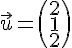
Pour 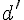
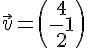
Pour que les droites soient parallèles, il faudrait qu’il existe un scalaire 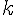
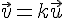
Cependant, cela donnerait le système suivant :
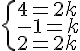
Les équations ne peuvent pas être satisfaites simultanément, donc 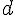
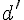
b) Étudier l’intersection de 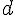
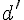
Pour étudier l’intersection, on résout le système :
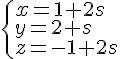
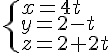
En résolvant les équations pour 


Équation 1 : 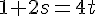
Équation 2 : 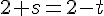
Équation 3 : 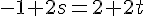
Résolvons l’équation 2 :
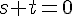
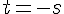
Substituons dans l’équation 1 :
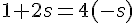
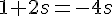
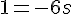
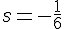
Donc 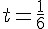
Vérifions avec l’équation 3 :
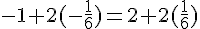
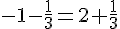
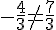
Il n’y a pas de solution commune, donc les droites 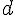
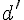
Exercice 8 – déterminer le point d’intersection de d et d ‘.
Pour la droite d :
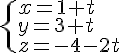
Pour la droite d’ :
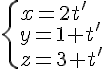
Pour que d et d’ se coupent, leurs équations doivent être égales :
1. Égalité des abscisses :
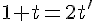
2. Égalité des ordonnées :
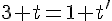
3. Égalité des cotes :
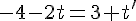
Résolvons ces équations :
De l’équation 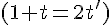
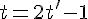
De l’équation 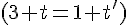
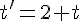
En substituant 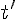
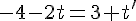
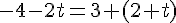

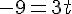

Substituons 
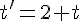
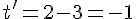
Point d’intersection :
Avec 
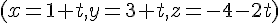
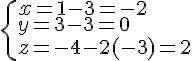
Le point d’intersection est donc : 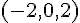
Exercice 9 – déterminer une représentation paramétrique de la droite (EF).
a) Représentation paramétrique de la droite (EF) :
La droite (EF) passe par les points E(1 ; 0 ; 3) et F(3 ; -1 ; 2). Le vecteur directeur de la droite (EF) est donné par :
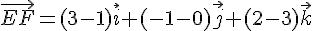
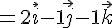
Une représentation paramétrique de la droite (EF) est donc :
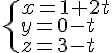
b) Exist-il des valeurs de a et b pour lesquelles M appartient à la droite (EF) ?
Le point M(a ; b ; -2) appartient à la droite (EF) si et seulement si il existe un paramètre 
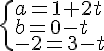
De l’équation 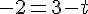
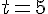
Substituons 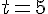
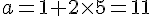
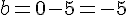
Ainsi, le point M(11 ; -5 ; -2) appartient à la droite (EF).
Exercice 10 – déterminer une représentation paramétrique de chaque droite.
a) Coordonnées des sommets :
A : 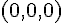
B : 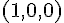
C : 
D : 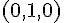
E : 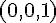
F : 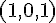
G : 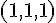
H : 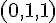
b) Représentation paramétrique :
Droite (AG) :
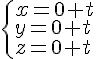
avec 
Droite (BH) :
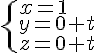
avec 
Télécharger ou imprimer cette fiche «les équations paramétriques et cartésiennes de droites : corrigé des exercices de maths en terminale en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.