Limites de fonctions : corrigé des exercices de maths en terminale en PDF
Mis à jour le 25 novembre 2025
Dans cet article, nous aborderons les limites de fonctions, un concept fondamental en maths pour les élèves de terminale. Comprendre les limites est crucial pour maîtriser des notions avancées comme la continuité et la dérivation, tout en développant des compétences analytiques essentielles. En explorant des exercices corrigés, vous renforcerez vos acquis et préparerez efficacement votre baccalauréat. Ne négligez pas cette étape clé pour réussir dans vos études scientifiques !
Exercice 1 – limite de fonctions et racines carrées.
1) Calculer : 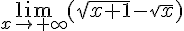
On multiplie et divise par le conjugué :
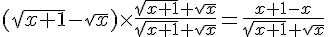
On simplifie et calcule la limite :


2) Calculer : 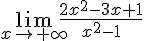
On divise numérateur et dénominateur par 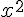
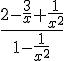
En passant à la limite, on obtient :
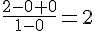
3) Calculer : 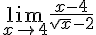
Factorisons en haut et simplifions :
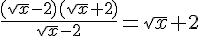
Exercice 2 – calculer ces limites.
1) Réponse : 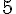
2) Réponse : 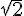
3) Réponse : 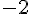
4) Réponse : 
5) Réponse : 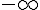
6) Réponse : 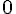
7) Réponse :
8) Réponse : 
Exercice 3 – déterminer la limite en l’infini.
1)
2)
3) 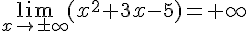
4)
5) 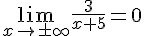
6)
7)
8) 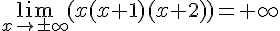
9)
10) 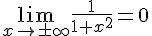
11)
12)
Exercice 4 – limite de f à gauche.
1) Fonction 
À gauche de 

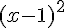
Donc, 
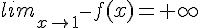
2) Fonction 
À gauche de 

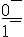
Donc, 
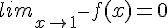
3) Fonction 
Le dénominateur se factorise en 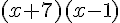
À gauche de 

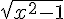
Donc, 
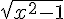

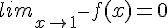
4) Fonction 
À gauche de 


Exercice 5 – justifier que ces implications sont fausses.
1) Contre-exemple : Soit 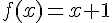
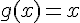
Alors, 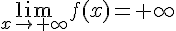
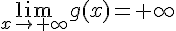

2) Contre-exemple : Soit 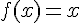
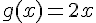
Alors, 
3) Contre-exemple : Soit 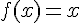
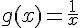
Alors, 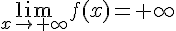
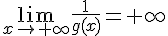
mais 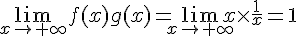
Exercice 6 – implications vraies ou fausses ?.
1) Si 
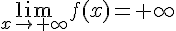
VRAI. Si 

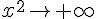
donc 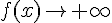
2) Si 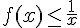
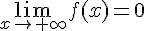
VRAI. Si 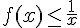

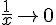
donc 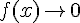
3) Si 
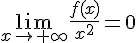
VRAI. Si 

le terme 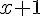
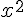
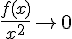
Exercice 7 – déduire l’équation d’une asymptote.
1) La limite 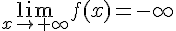
2) La limite 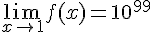
3) La limite 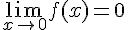
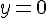
4) La limite 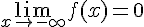
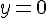
5) La limite 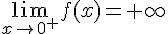
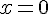
6) La limite 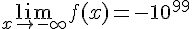
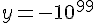
Exercice 8 – limites de f en 1 à droite et à gauche.
1) Justifier que f n’est pas continue sur 
Pour que la fonction 

- La limite de
- Ces limites doivent être égales à
Observons le graphe :
, mais il y a une discontinuité en
.
2) Donner les valeurs de 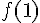
La valeur de 
Calculons les limites :
- Limite à gauche (quand
- Limite à droite (quand
3) Que doit valoir 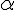

Pour que 

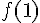
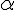
Donc, 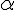
Exercice 9 – fonction cube et calculs de limites.
1) Limites de la fonction cube :
La fonction cube est définie par 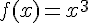
Les limites aux bornes de l’infini sont :
Lorsque 
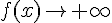
Lorsque 
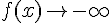
2) Tableau de variation de la fonction cube :
La fonction 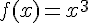

On peut représenter les variations dans un tableau comme suit :
| x | 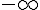
|
0 | 
|
|---|---|---|---|
| f(x) | 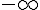
|
0 | 
|
3) Justification des solutions :
a) Pour résoudre 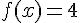
![x\in[1,5;1,6]](https://maths-pdf.fr/latex-images/1ab1c98d298c0eaa4288009872895c20.png)


En résolvant, on obtient ![x=\sqrt[3]{4}](https://maths-pdf.fr/latex-images/6836d47cdc48efa4be773b0bd21dd3de.png)
La seule solution dans l’intervalle donné est 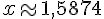
b) Pour résoudre 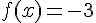


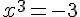
La solution est ![x=\sqrt[3]{-3}](https://maths-pdf.fr/latex-images/a98d9edc05103c35090f1a47f810b506.png)
Cela donne une unique solution 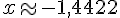
Exercice 10 – fonction valeur absolue.
1) Représentation graphique :
La fonction partie entière ![[x]](https://maths-pdf.fr/latex-images/3e5314e9fd31509fdeb83faa0f729ba2.png)

2) Résolution :
a) ![[x]=\frac{1}{2}](https://maths-pdf.fr/latex-images/e4d07e23f0703884da15996f8159d53c.png)
![[x]](https://maths-pdf.fr/latex-images/3e5314e9fd31509fdeb83faa0f729ba2.png)
b) ![[x]=1](https://maths-pdf.fr/latex-images/13326a511670cd532aa06e8effe0ced2.png)
Les solutions sont les nombres réels tels que 
Télécharger ou imprimer cette fiche «limites de fonctions : corrigé des exercices de maths en terminale en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.











 , mais il y a une discontinuité en
, mais il y a une discontinuité en 





