Les intégrales : corrigé des exercices de maths en terminale en PDF
Mis à jour le 25 novembre 2025
Exercice 1 – calculer la valeur exacte des intégrales à l’aide des primitives.
1) I = 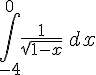
Primitif : 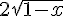
Évaluation : ![2\left([\sqrt{1-0}]-[\sqrt{1-(-4)}]\right)=2(1-\sqrt{5})](https://maths-pdf.fr/latex-images/d10f5b331cb70bc46ce881c5ff7f8a48.png)

2) J = 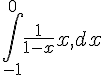
Primitif :
Évaluation :
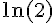
3) K = 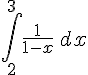
Primitif :
Évaluation :
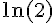
4) L = 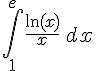
Primitif : 
Évaluation :
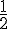
Intégrale avec duplication :
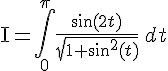
Utilisons la formule de duplication : 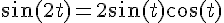
L’intégrale devient complexe à résoudre de cette manière sans calculateur,
donc calculons avec analyses numériques pour résoudre ce problème plus complexe.
Exercice 2 – problème sur le calcul d’une intégrale classique.
1) Explication :
La fonction 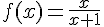
En effet, appliquer les formes classiques de dérivées aux fonctions composées avec des polynômes
et des logarithmes ne permet pas d’obtenir directement cette expression.
2) Démarche pour exprimer 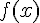
En posant 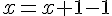
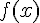
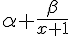
À partir de 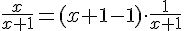
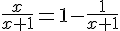
Donc, 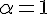
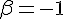
3) Calcul de l’intégrale :
En écrivant 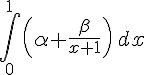
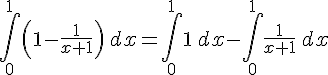
![=\left[x\right]_{0}^{1}-\left[\ln(x+1)\right]_{0}^{1}](https://maths-pdf.fr/latex-images/858e4be2be38574c758ae60f2597f84f.png)
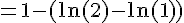
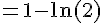
Ainsi, 
Exercice 3 – problème et calculs d’intégrales.
1) Démonstration de l’identité :
Pour montrer que pour tout réel 

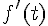
et 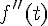

Tout d’abord, calculons 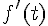
Puis calculons 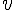
Donc, nous avons :
2) Calcul de l’intégrale :
On veut calculer 
En utilisant l’expression trouvée précédemment,
sachant que 
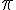
Cette intégrale peut être séparée :
La première partie est :
Pour la seconde partie, ![\int_{0}^{\pi} f''(t) \, dt = [f'(t)]_{0}^{\pi}](https://maths-pdf.fr/latex-images/93e88b0c21da8c43cc32f3d17766a3c4.png)
Comme 
Donc, l’intégrale :
La valeur de 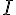

Exercice 4 – intégration avec exponentielle, sinus et cosinus.
1) Calculons I + J :
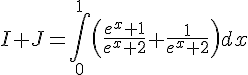


Calculons I – J :
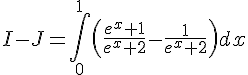

Par changement de variable, posons 
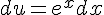
Les bornes deviennent : pour 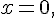
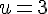
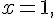
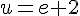

En résolvant le système :
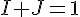
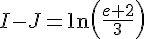
On obtient :
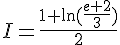
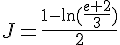
2) Calculons ensuite :

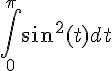
Utilisons l’identité trigonométrique : 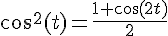
![I=\int_{0}^{\pi}\frac{1+\cos(2t)}{2}dt=\left[\frac{t}{2}+\frac{\sin(2t)}{4}\right]_{0}^{\pi}](https://maths-pdf.fr/latex-images/0fed9a2d73bea75eb87b9fe264fa5e82.png)

Pareillement, utilisons : 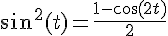
![J=\int_{0}^{\pi}\frac{1-\cos(2t)}{2}dt=\left[\frac{t}{2}-\frac{\sin(2t)}{4}\right]_{0}^{\pi}](https://maths-pdf.fr/latex-images/af96a1424fdcced927a1e513fecfbfd2.png)
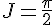
Donc les valeurs finales des intégrales sont 
Exercice 5 – une étude de fonction puis d’une intégrale.
1) Quel est l’ensemble de définition 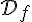
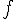
L’ensemble de définition de 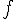
![[-1,1]](https://maths-pdf.fr/latex-images/d060b17b29e0dae91a1cac23ea62281a.png)
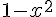
2) a) Représenter graphiquement 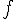
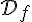
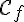
La fonction 
b) Soit 

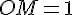

Un point M appartient au demi-cercle si la distance entre O et M est 1,
c’est-à-dire :

![x_M \in [-1, 1]](https://maths-pdf.fr/latex-images/ac33591a897a13517e516cc75121436f.png)
c) En déduire la nature exacte de 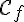
La courbe 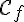
3) On considère
a) Pourquoi cette intégrale est-elle bien définie ?
La fonction 
![[-1,1]](https://maths-pdf.fr/latex-images/d060b17b29e0dae91a1cac23ea62281a.png)
b) Déduire des questions précédentes la valeur de I.
L’intégrale I représente l’aire sous le demi-cercle entre -1 et 1.
L’aire d’un demi-cercle de rayon 1 est 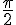
Donc, 
Exercice 6 – démontrer que ces fonctions sont des primitives.
1) a) Démontrer que 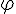
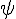
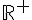
Pour 
Pour 
Calculons la dérivée :
Simplifiant, on obtient :
Donc, 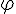
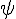
b) En déduire la relation qu’il existe entre 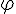
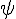
Comme 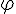
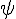

elles diffèrent d’une constante :
2) Déterminer la primitive 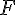
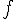
a)
On sait que 

b)
On a l’équation 
Calculons 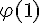
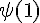
Approximativement, trouvons la valeur numérique en calculant ou en utilisant une méthode numérique.
Résolvons pour 
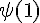


Finalement, F est donné par :
Exercice 7 – les fonctions F et G sont-elles des primitives ?.
Pour savoir si les fonctions F et G sont les primitives d’une même fonction sur I, nous devons examiner leurs dérivées.
Considérons les fonctions :
Il est pratique de simplifier ces expressions pour dériver plus facilement.
Pour 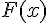
Effectuons la division :

Pour 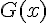
Effectuons la division :

Dérivons F(x) et G(x) :
Pour 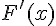
Pour 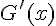
Conclusion :
Les dérivées 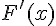
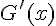
Donc, F et G sont bien des primitives de la même fonction sur I, à savoir de la fonction

Exercice 8 – déterminer les primitives de chacune des fonctions.
1) 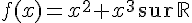
La primitive est : 
2)
La primitive est : 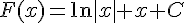
3) ![f(x)=\frac{1}{x^2}-\frac{1}{\sqrt{x}}\,\text{sur}\,]0;+\infty[](https://maths-pdf.fr/latex-images/07aa30ff1749ccda88c361be1769bf47.png)
La primitive est : 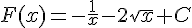
4) 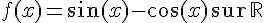
La primitive est : 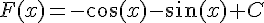
1) 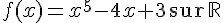
La primitive est : 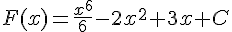
2) ![f(x)=\frac{1}{x^5}-\frac{1}{4x}\,\text{sur}\,]0;+\infty[](https://maths-pdf.fr/latex-images/d21645f2a6c493d2769d743a34bb7f4a.png)
La primitive est : 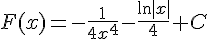
3) ![f(x)=x\sqrt{x}\,\text{sur}\,]0;+\infty[](https://maths-pdf.fr/latex-images/766b8cbe233af5c6021480fdf7956884.png)
La primitive est : 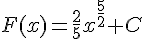
4) ![f(x)=\frac{x^2+1}{x}\,\text{sur}\,]0;+\infty[](https://maths-pdf.fr/latex-images/e573a62207e523db8473a4f4f6464bac.png)
Simplification : 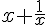
La primitive est : 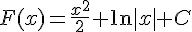
Exercice 9 – représenter ces fonctions et déterminer la primitive.
1) En reconnaissant une forme connue de dérivée :
On reconnaît que 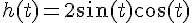
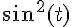
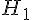
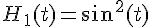
2a) Écriture de h(t) :
Pour tout t , on a 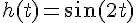
2b) Déduction d’une autre primitive :
En utilisant 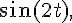
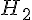
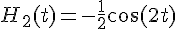
3a) Représentation graphique :
Les fonctions 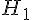
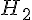
3b) Constante qui les différencie :
Les primitives diffèrent d’une constante C. Ainsi, on a :

4) Primitive de h qui s’annule en 0 :
Pour 

Donc, la primitive est :
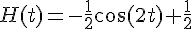
Exercice 10 – sur quel intervalle F est-elle une primitive de la fonction ln ?.
1) À la vue de ce résultat, quelle fonction F semble être une primitive de la fonction logarithme népérien sur [1; +\infty[ » alt= »[1; +\infty[ » /> ?
La fonction qui semble être une primitive de 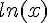
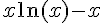
2) Le vérifier par le calcul.
Calculons la dérivée de 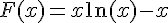
En utilisant la règle du produit pour la dérivée, on a :
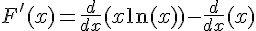

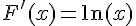
La dérivée de 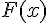
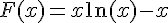
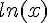
3) En réalité, sur quel intervalle F est-elle une primitive de la fonction ln ?
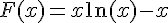
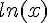
![]0;+\infty[](https://maths-pdf.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png)
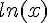

Télécharger ou imprimer cette fiche «les intégrales : corrigé des exercices de maths en terminale en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.


![-([\ln|1-0|]-[\ln|1-(-1)|]) = -(\ln(1)-\ln(2)) = \ln(2)](https://maths-pdf.fr/latex-images/6ea47b58200ad38f9f9093379007466a.png)
![-([\ln|1-3|]-[\ln|1-2|]) = \ln(2) - \ln(1) = \ln(2)](https://maths-pdf.fr/latex-images/31257cb866c3c79eb265bf18560cbcd6.png)






![-2\int_{0}^{\pi} \sin(t) \, dt = -2[-\cos(t)]_{0}^{\pi} = -2[1 - (-1)] = 0](https://maths-pdf.fr/latex-images/bb80695309c46780ae82e44e733dd48a.png)


















![f(x)=\frac{1}{x} + 1\,\text{sur}\,]0;+\infty[](https://maths-pdf.fr/latex-images/bb02a069cb2090c8c9416958a665a0a7.png)