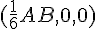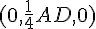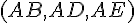Vecteurs de l’espace : corrigé des exercices de maths en terminale en PDF
Mis à jour le 25 novembre 2025
Dans cet article consacré aux vecteurs de l’espace, nous allons corriger divers exercices de mathématiques essentiels pour les élèves de terminales. La maîtrise de ce concept permet non seulement d’améliorer la compréhension des espaces vectoriels, mais également de développer des compétences clés en géométrie et en algèbre. Ces notions sont fondamentales pour réussir le baccalauréat et pour aborder des études supérieures en sciences et en ingénierie.
Exercice 1 – pyramide de sommet A et vecteurs.
a) Exprimer le vecteur 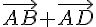
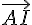
Puisque 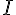
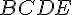
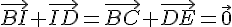
Or, 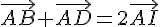
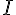
b) Démontrer que 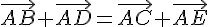
Dans un parallélogramme, la somme des vecteurs joignant un sommet aux points d’intersection des diagonales est égale à la somme des vecteurs joignant ce sommet aux autres sommets opposés. Ainsi, nous avons :
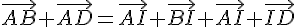
En développant, nous trouvons que 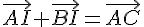
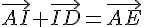
Donc, 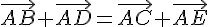
Exercice 2 – parallélépipède rectangle et égalité de vecteurs.
a) Justification :
Dans un parallélépipède rectangle, les milieux des arêtes non parallèles permettent d’obtenir des égalités vectorielles par la relation de Chasles.
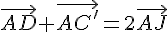
Parce que 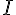
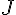
![[AB]](https://maths-pdf.fr/latex-images/5e32d4dbe98ef3af1b5123ccba43cbf7.png)
![[C'D']](https://maths-pdf.fr/latex-images/cc53fcdfbdf6188c17a18daa1518f3b8.png)
De même, 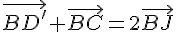
b) Démonstration :
En appliquant la relation de Chasles, nous pouvons écrire :
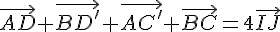
car chaque paire de vecteurs constitue deux fois le vecteur formé par les milieux, conformément à la géométrie du parallélépipède rectangle.
Exercice 3 – cube et milieux d’arêtes.
1. Démontrer que : 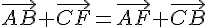
Utilisons la relation de Chasles sur le cube.
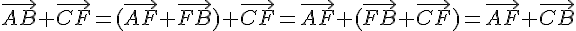
2. I est le milieu de l’arête [FG]. Quel est le point M tel que : 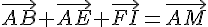
Comme I est le milieu de [FG], on a : 
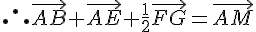
Le point M est donc le point du cube obtenu par translation de vecteur 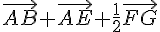
3. Quel est le vecteur 
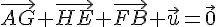
Simplifions l’équation :
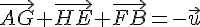
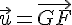
4. J et K sont les milieux respectifs des arêtes [AB] et [AE]. Quel est le point M tel que : 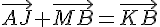
Écrivons les vecteurs en fonction des coordonnées des milieux :
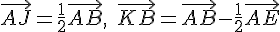
En réarrangeant :
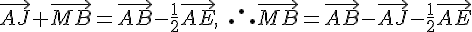
Donc, M est un point à l’intérieur du cube tel que M est à mi-chemin entre B et la projection orthogonale de K.
Exercice 4 – démontrer que la droite est orthogonale au plan.
1) Pour démontrer que la droite (BC) est orthogonale au plan (ADI) :
Dans un tétraèdre régulier, tous les arêtes ont la même longueur et toutes les faces sont des triangles équilatéraux. Le plan (ADI) est le plan médiateur du segment [BC]. Par définition, ce plan est orthogonal au segment [BC] en son milieu I.
Comme I est le milieu de [BC] et que (ADI) est le plan médiateur, chaque point de (ADI) est équidistant de B et C. Cela signifie que la droite (BC) est perpendiculaire au plan (ADI). Ainsi, on a :
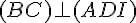
2) En déduire que (BC) ⊥ (AD) :
Comme nous l’avons démontré, le plan (ADI) est orthogonal à (BC), et (AD) appartient au plan (ADI). Cela implique que la droite (BC) est orthogonale à toute droite située dans le plan (ADI) et passant par le point de contact avec (BC). Par conséquent :

Exercice 5 – les propositions sont-elles vraies ou fausses ?.
1) 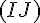
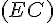
Pour démontrer l’orthogonalité, nous devons montrer que le produit scalaire des vecteurs 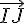
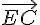
Coordonnées :
– 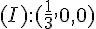
– 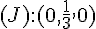
– 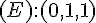
– 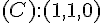
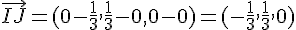
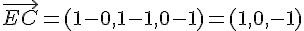
Produit scalaire : 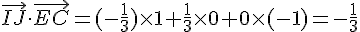
Le produit scalaire n’est pas nul, donc faux.
2) 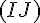
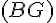
Coordonnées :
– 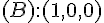
– 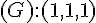
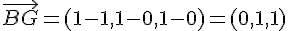
Produit scalaire : 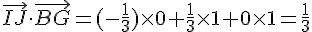
Le produit scalaire n’est pas nul, donc faux.
3) 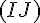
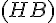
Coordonnées :
– 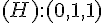
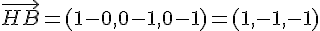
Produit scalaire : 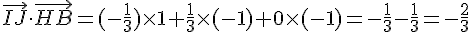
Le produit scalaire n’est pas nul, donc faux.
4) 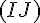
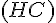
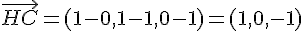
Produit scalaire : 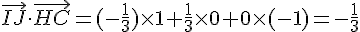
Le produit scalaire n’est pas nul, donc faux.
Conclusion: Toutes les propositions sont fausses.
Exercice 6 – déterminer la valeur de t pour laquelle la longueur est minimale.
a) Exprimons les coordonnées de M en fonction de t : Si 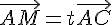
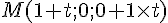
b) La longueur 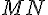

Ce qui simplifie à :
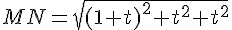
c) Pour minimiser 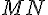
![\frac{d}{dt}[\sqrt{(1+t)^2+t^2+t^2}]=0](https://maths-pdf.fr/latex-images/7423c3b1f900eb57b6bcf164737e9ca0.png)
Après calcul, cela donne 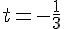
Donc, la valeur de 
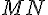
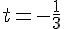
Exercice 7 – déterminer les coordonnées du point M tel que la distance AM soit minimale.
1) Les points A(5;2;6) et B(5;-6;4) appartiennent-ils à la droite 
Pour qu’un point 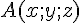


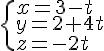
Pour le point 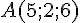
Équation en 
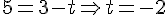
Équation en 
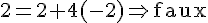
Donc, 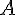

Pour le point 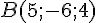
Équation en 
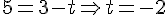
Équation en 
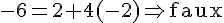
Donc, 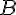

2) Déterminer les valeurs des réels 

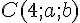

Équation en 
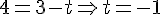
Équation en 
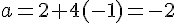
Équation en 
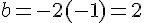
Donc, 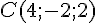

3) Soit 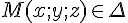
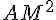

Les coordonnées de 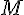
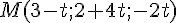
La distance au carré est :
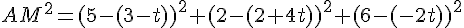
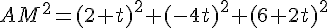
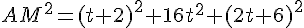
4) Déterminer les coordonnées du point M tel que la distance AM soit minimale.
Pour minimiser 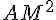
On développe : 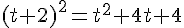
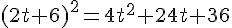
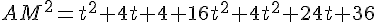
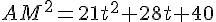
La dérivée est : 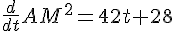
On résout : 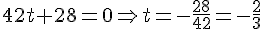
Coordonnées minimales du point 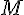
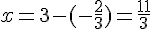
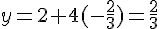
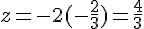
Donc, le point 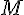
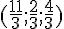
Exercice 8 – démontrer que la droite et le plan sont sécants.
1) Vérification que les points A, B et C définissent un plan :
Pour vérifier que les points A(-2; 0; 1), B(1; 2; -1) et C(-2; 2; 2) définissent un plan, nous devons montrer qu’ils ne sont pas colinéaires. Pour cela, calculons deux vecteurs dans le plan :
Vecteur 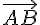

Vecteur 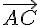
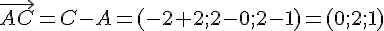
Calculons le produit vectoriel 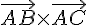
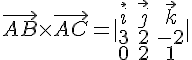
En développant le déterminant, nous obtenons :
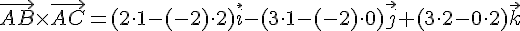
= 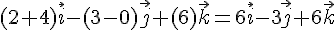
Le vecteur 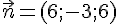
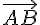
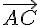
2) Démonstration que la droite (DE) et le plan (ABC) sont sécants :
Considérons la droite (DE) définie par les points D(-2; -1; 0) et E(-2; 5; 2). Le vecteur directeur de (DE) est :
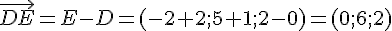
Une équation paramétrique de la droite (DE) est donc :
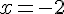
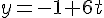
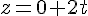
Pour montrer que la droite est sécante avec le plan (ABC), qui a pour vecteur normal 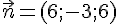
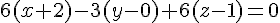
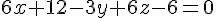
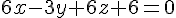
Remplaçons x, y et z par les équations paramétriques de la droite (DE) :
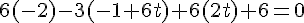
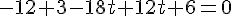
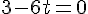
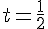
En remplaçant 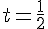
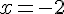
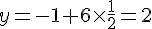
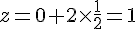
Le point d’intersection I a pour coordonnées (-2; 2; 1).
Exercice 9 – déterminer la section du pavé par un plan.
1) Représentation paramétrique du plan (IJG) :
Les coordonnées de I, J et G sont :
- I :
- J :
- G :
Une équation paramétrique du plan (IJG) est donnée par :
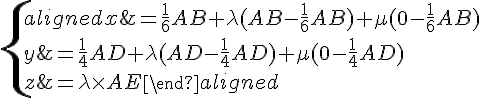
2) Coordonnées du point d’intersection L du plan (IJG) et de la droite (BF) :
On sait que :
B : 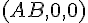
F : 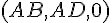
Équation paramétrique de la droite (BF) :
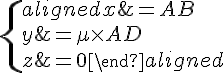
En résolvant pour l’intersection avec le plan (IJG), on remplace dans les équations du plan :
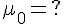
Déterminer 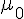
3) Représentation graphique :
Consulter le graphe pour voir la section section du pavé par le plan (IJG).
Exercice 10 – etudier la position de la droite.
1) Cas 1 :
Les vecteurs directeurs des droites sont respectivement :
Pour 
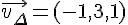
Pour 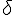
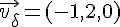
Calculons le produit vectoriel :
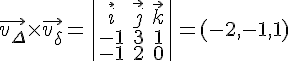
Le produit vectoriel est non nul, donc 
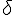
Déterminons s’il existe un point commun en résolvant :
En résolvant ce système, nous trouvons qu’il n’y a pas de solution. Donc, 
2) Cas 2 :
Vecteurs directeurs :
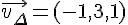
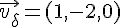
Produit vectoriel :
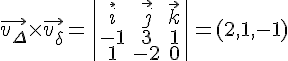
Le produit vectoriel est non nul, donc non parallèles.
Résolution :
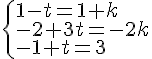
Pas de solution commune. 
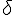
3) Cas 3 :
Vecteurs directeurs :
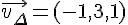
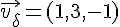
Produit vectoriel :
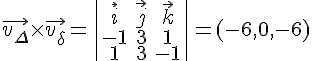
Le produit vectoriel est non nul, donc non parallèles.
Résolution :
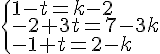
Pas de solution commune. 
Télécharger ou imprimer cette fiche «vecteurs de l'espace : corrigé des exercices de maths en terminale en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.