Droites et plans de l’espace : corrigé des exercices de maths en terminale en PDF
Mis à jour le 25 novembre 2025
Exercice 1 – position relative des droites dans un cube.
Les droites 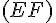

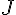

![[EF]](https://maths-pdf.fr/latex-images/17e8d8206f8e7df67a64bc00effc1ef0.png)
![[FG]](https://maths-pdf.fr/latex-images/237cdfdcacceafa47d52196151dc42f3.png)
Ainsi, le vecteur 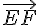

Nous pouvons aussi constater que les longueurs ![[EF]](https://maths-pdf.fr/latex-images/17e8d8206f8e7df67a64bc00effc1ef0.png)
![[HK]](https://maths-pdf.fr/latex-images/8d9662b5d6108a590f7152c17b72fa88.png)
En conclusion, 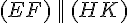
Exercice 2 – déterminer et construire la section d’un cube.
1er Cas :
Dans le premier cas, on considère que:
Pour déterminer et tracer la section du cube par le plan 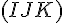
Ce triangle représente la section du cube par le plan requis.
2ème Cas :
Dans le second cas, on a :
Pour déterminer et tracer la section du cube par le plan 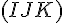
Ce triangle représente la section du cube par le plan requis.
Exercice 3 – construire la section de la pyramide.
1) Reproduction de la figure :
N’oubliez pas de placer les points I et J qui sont les milieux des segments ![[SD]](https://maths-pdf.fr/latex-images/19a43c54ba1f8dbe1397d857e0d1274a.png)
![[AB]](https://maths-pdf.fr/latex-images/5e32d4dbe98ef3af1b5123ccba43cbf7.png)
Cela signifie que les coordonnées de ces points sont obtenues en prenant la moyenne des coordonnées des extrémités de chaque segment.
2) Construction de la section par le plan 
Pour construire la section de la pyramide par le plan 
- Tracer le segment
- Tracer le segment
- La droite passant par
La section est alors un triangle formé par les points 
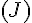
Justification : Le plan 
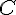
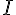
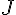
En coupant la pyramide par ce plan, la section obtenue sera un triangle car chaque sommet du triangle appartient à une arete différente de la pyramide.
Exercice 4 – quelle est la nature de cette section ?.
1) Reproduction de la figure :
Reproduisez le tétraèdre régulier 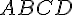
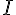
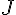

qui sont les milieux des segments ![[BC]](https://maths-pdf.fr/latex-images/25c6a1f25bc97657699ccfd396989bfd.png)
![[AB]](https://maths-pdf.fr/latex-images/5e32d4dbe98ef3af1b5123ccba43cbf7.png)
![[AD]](https://maths-pdf.fr/latex-images/afbbed58216cc750d889958a8effb615.png)
2) Construction de la section par le plan 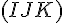
Le plan 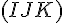
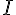
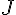

ce qui aide à déterminer la section, puisque chaque paire de ces points est équidistante des sommets correspondants du tétraèdre.
3) Nature de la section :
La section du tétraèdre par le plan 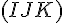
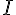
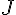

Le plan passant par ces trois points forme une section triangulaire, qui est en fait un triangle médian du tétraèdre.
Ce triangle est un triangle équilatéral car le tétraèdre est régulier.
Exercice 5 – citer des droites orthogonales.
1) Citer six droites orthogonales à la droite (EA) :
Les droites orthogonales à (EA) sont : (AB), (AD), (EF), (EH), (BC) et (FG).
2) Citer six droites orthogonales à la droite (EB) :
Les droites orthogonales à (EB) sont : (AB), (BC), (EH), (ED), (AF) et (HG).
3) Citer deux droites orthogonales au plan (BCG) :
Les droites orthogonales au plan (BCG) sont : (AE) et (DH).
4) Citer deux droites orthogonales au plan (AFG) :
Les droites orthogonales au plan (AFG) sont : (BC) et (DH).
1) Démontrer que la droite (AB) est orthogonale au plan (BCG) :
La droite (AB) est orthogonale au plan (BCG) car elle est perpendiculaire aux droites (BC) et (BG) qui appartiennent à ce plan.
2) En déduire que les droites (AB) et (CF) sont orthogonales :
La droite (CF) est dans le plan (BCG), et comme (AB) est orthogonale à ce plan, elle est donc orthogonale à toute droite dans ce plan, y compris (CF).
Exercice 6 – tracer l’intersection du plan et d’une face.
1) Pour reproduire la figure de l’exercice précédent, assurez-vous d’avoir une représentation claire du pavé ABCDEFGH.
2) Pour tracer l’intersection du plan 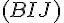
Reliez ces points pour tracer la ligne d’intersection.
3) Pour la face DCGH, appliquez le même principe :
trouvez les points d’intersection du plan 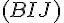
4) Finalement, pour terminer la construction de la section du pavé ABCDEFGH par le plan 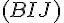
reliez les intersections trouvées précédemment pour dessiner la section complète.
Exercice 7 – construire la section d’un cube par le plan (IJK).
1. Section par le plan (EIJ) :
Le plan est défini par les points E, I, J, qui sont des points spécifiques entre les sommets du cube.
Position des points :
- I est situé sur
- J est situé sur
Pour tracer la section du cube par le plan (EIJ), déterminez les points d’intersection du plan avec les arêtes du cube qui passent par E, I, et J.
Reliez ces points pour représenter la section.
2. Section par le plan (IJK) :
Position des points :
- I est situé sur
- J est situé sur
- K est situé sur
Pour tracer la section du cube par le plan (IJK), trouvez les points d’intersection que le plan a avec les arêtes du cube passant par I, J, et K.
Reliez ensuite ces points d’intersections pour représenter la section.
Exercice 8 – section et construction .
Première situation :
1. Détermination des points
Le cube est noté 
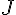

![[BC]](https://maths-pdf.fr/latex-images/25c6a1f25bc97657699ccfd396989bfd.png)
![[EH]](https://maths-pdf.fr/latex-images/70e4cc76690134f18386d4823f150858.png)
2. Construction de la section
Pour construire la section, tracez le plan passant par les points 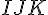
Ce plan coupe le cube selon un quadrilatère.
Conclusion : La section est déterminée par les points 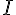
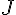

![[AB]](https://maths-pdf.fr/latex-images/5e32d4dbe98ef3af1b5123ccba43cbf7.png)
Deuxième situation :
1. Détermination des points
Les points sont définis comme suit :
2. Construction de la section
Tracez le plan passant par les points 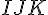
Conclusion :
La section du cube par le plan 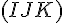
Exercice 9 – donner les coordonnées des vecteurs.
1) Calcul des coordonnées des vecteurs:
Pour le vecteur 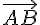
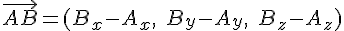
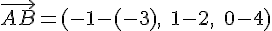

Pour le vecteur 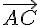
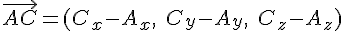
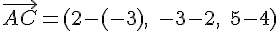
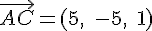
Pour le vecteur 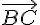

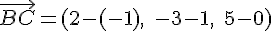
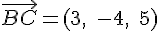
2) Calcul des coordonnées des vecteurs 

Pour le vecteur 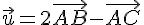
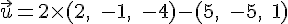
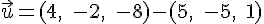
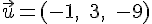
Pour le vecteur 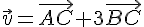
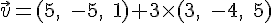

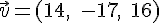
Exercice 10 – déterminer les coordonnées du vecteur.
1) Déterminer les coordonnées du point C défini par 
Le vecteur 


Les coordonnées du point C sont obtenues en ajoutant celles du vecteur 
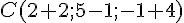
Soit 
2) Déterminer les coordonnées du vecteur 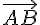
Le vecteur 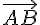

Puisque ABCD est un parallélogramme, 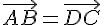
Donc, pour trouver D, on ajoute 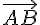

3) Déterminer les coordonnées du centre K de ce parallélogramme.
Le centre K d’un parallélogramme est le milieu des diagonales 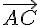
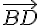
On calcule d’abord les points correspondants :
Pour le milieu K des coordonnées 

En appliquant les coordonnées des points A, B, C et D :

Après calcul, on obtient :
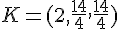
Soit 
Télécharger ou imprimer cette fiche «droites et plans de l'espace : corrigé des exercices de maths en terminale en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.

![[GH]](https://maths-pdf.fr/latex-images/8a8d0adbf34223b9213ef6f0468eb436.png)
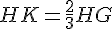
![I\in[AD]](https://maths-pdf.fr/latex-images/3820ebca2f54e2664a79aa5150f31afe.png)
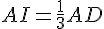
![J\in[FG]](https://maths-pdf.fr/latex-images/e6d14e4baf468128419ccc23e0b83a83.png)
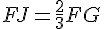
![K\in[AB]](https://maths-pdf.fr/latex-images/af83f75ef277cc7864b8fbef42e12592.png)
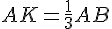
![[CI]](https://maths-pdf.fr/latex-images/9a9af12be0790a90ace380a2fe2fdf4d.png)
![[CJ]](https://maths-pdf.fr/latex-images/672977f90c83f2ca345873308d079acf.png)

![[HD]](https://maths-pdf.fr/latex-images/8ac5e59cdaa2b2074160972f57b78686.png)




![[HG]](https://maths-pdf.fr/latex-images/13e5832f5571902e48f6615c9aa80eb0.png)

![I\in[AE]](https://maths-pdf.fr/latex-images/be31e6051ed7f4ff972662cfebee2b37.png)
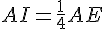
![J\in[DH]](https://maths-pdf.fr/latex-images/708e17a4cb35ea72ab207f84e7b7d853.png)
![K\in[FG]](https://maths-pdf.fr/latex-images/2e672287aa5dca50354a814f47f748bf.png)