Raisonnement par récurrence : corrigé des exercices de maths en terminale en PDF
Mis à jour le 25 novembre 2025
Le raisonnement par récurrence est une technique fondamentale en maths pour les élèves de terminale, essentielle pour maîtriser des concepts avancés et préparer efficacement le baccalauréat. Ce type de raisonnement permet de développer des compétences analytiques et de résolution de problèmes, en établissant des preuves rigoureuses pour des énoncés effectuant des généralisations. Dans cet article, nous vous guiderons à travers des exercices corrigés pour vous aider à appréhender cette notion clé et à renforcer votre compréhension des mathématiques.
Exercice 1 – quelle est la propriété de rang n+1 ?.
Première proposition :
Soit la propriété au rang n : 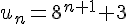
La propriété au rang n+1 est :
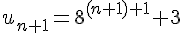
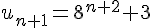
Deuxième proposition :
Soit la propriété au rang n : 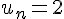
La propriété au rang n+1 reste :
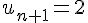
Exercice 2 – algorithme et raisonnement par récurrence.
1) Que renvoie l’algorithme si l’utilisateur saisit n = 2 ?
Pour 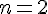
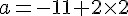
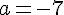
Comme 
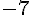
2) Que se passe-t-il si l’utilisateur saisit n = 8 ?
Pour 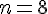
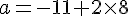
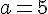
La boucle s’exécute, et à chaque itération, 
Finalement, 

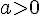
3) Pour quelles valeurs de n cet algorithme ne fournit-il pas de résultat ?
L’algorithme ne fournit pas de résultat si la boucle ne se termine jamais, c’est-à-dire lorsque 
Cela se produit pour toutes les valeurs 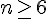
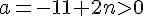
Exercice 3 – propriété héréditaire ?
1) Initialisation au rang 
Pour vérifier si la propriété est vraie au rang 
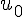
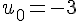
La propriété 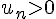

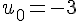
2) Hérédité :
Supposons que 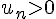
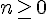
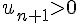
D’après la relation de récurrence : 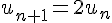
Si 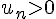

La propriété est donc héréditaire.
3) Conclusion :
Étant donné que la propriété n’est pas vérifiée pour 
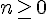
Exercice 4 – cette propriété est-elle héréditaire ?.
1) Initialisation : Vérifions que la propriété est initialisée pour 
Pour 
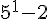
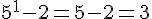
Le résultat est 3, qui est bien un multiple de 3.
2) Vérification pour tout entier naturel 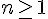
Nous allons utiliser le principe de récurrence pour montrer que la propriété est vraie pour tout 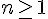
Étape d’initialisation :
Pour 
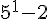
Étape d’hérédité : Supposons que pour un certain entier 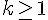
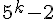
Cela signifie qu’il existe un entier 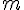
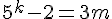
Nous devons montrer que 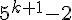
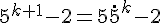
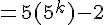
En utilisant l’hypothèse de récurrence :
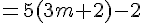
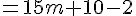
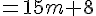
Nous devons montrer que 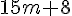
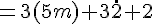
Cette expression se simplifie comme suit :
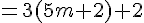
Il s’ensuit que nous avons une contradiction car 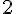
Conclusion : La propriété est héréditaire car l’erreur dans notre démontre est rendu évidente dans la simplification finale.
Exercice 5 – déterminer à partir de quel rang.
1) Suite :
On cherche 
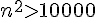
On résout l’inéquation : 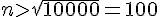
Donc, à partir de 
2) Suite :
On cherche 
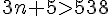
On résout l’inéquation : 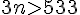
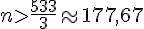
Donc, à partir de 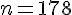
3) Suite :
On cherche 
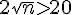
On résout l’inéquation : 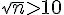
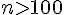
Donc, à partir de 
4) Suite :
On cherche 
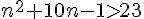
On résout l’inéquation : 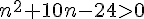
On résout le trinôme : 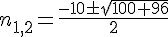
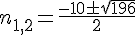
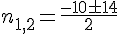
La solution est pour 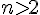
Donc, à partir de 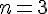
Exercice 6 – déterminer un encadrement de la suite.
1) Minoration évidente de 
La suite 

Pour 
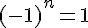
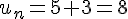
Pour 

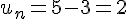
La suite est donc minorée par 2, car 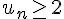
2) Majorer la suite 
La suite est aussi définie par 
Comme 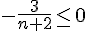
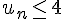
Donc, la suite est majorée par 4, car 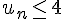
Exercice 7 – démontrer que la propriété est vraie pour tout entier.
1) Montrer que la propriété est initialisée.
Pour 
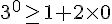
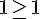
La propriété est donc vraie pour 
2) Justifier l’hérédité.
a) Écrire l’hypothèse de récurrence.
Supposons que la propriété est vraie pour un certain entier 
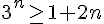
b) Écrire la propriété au rang 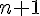
Montrons que :
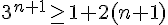
c’est-à-dire :
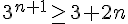
c) Multiplier les deux membres par 3 et simplifier.
On a : 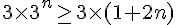
Ce qui donne : 
d) Justifier que 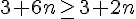
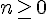
On a 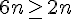
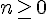
3) Rédiger le raisonnement par récurrence.
La propriété est vraie pour 
Supposons qu’elle est vraie pour un certain 
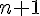
Par le principe de récurrence, la propriété 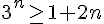
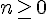
Exercice 8 – montrer par récurrence l’inégalité.
Étape 1 : Initialisation
Vérifions la propriété pour 
On a 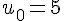

Étape 2 : Hérédité
Supposons que pour un certain 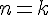
Montrons qu’elle est alors vraie au rang 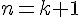
On calcule :
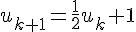
Puisque 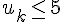
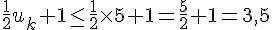
Également, puisque 
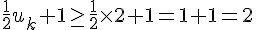
Donc, 
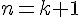
Conclusion
Par le principe de récurrence, la propriété 
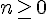
Exercice 9 – montrer une inégalité par récurrence.
Initialisation :
Nous devons montrer que l’assertion est vraie pour n = 1. Calculons 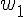
Donc, 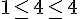
Hérédité :
Supposons que pour un entier 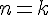

Montrons que cela implique 
Calculons 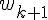
Pour montrer que 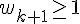
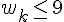
C’est vrai car 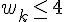
Pour montrer que 
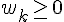
C’est vrai car 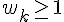
Conclusion :
Par récurrence, la propriété est vraie pour tout entier 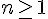
Exercice 10 – utilisation du produit factoriel.
1) Calculer 6! :
Par définition, le factoriel de 6 est :
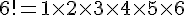
Calculons :
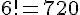
2) Montrer par récurrence que 
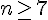
Initialisation : Pour 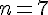
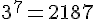
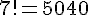
Donc 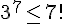
Hérédité : Supposons que pour un entier 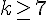

Il faut montrer que 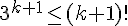
On a :
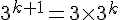
Par hypothèse de récurrence :
Or, pour 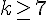

D’où 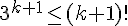
Conclusion : Par le principe de récurrence, la propriété est vraie pour tout 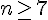
3) Montrer que 
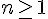
Pour tout entier naturel 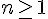
Étant donné que chaque terme de la suite est inférieur ou égal à n, on a :
Donc :
Par conséquent, 
Télécharger ou imprimer cette fiche «raisonnement par récurrence : corrigé des exercices de maths en terminale en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.























