La continuité : corrigé des exercices de maths en terminale en PDF
Mis à jour le 25 novembre 2025
Exercice 1 – fonctions rationnelles et asymptotes.
1) a) Détermination de 

On sait que 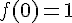
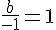
Donc, 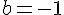
On sait aussi que 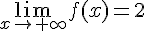
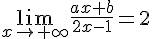
On en déduit que 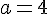
b) Expression de 
En utilisant les valeurs de 

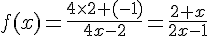
2) Détermination des asymptotes à 
Asymptote horizontale : 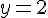
Asymptote verticale : 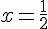
3) Calcul de 

Le signe de 
4) Tableau de variation de 
Sur ![]-\infty;\frac{1}{2}[](https://maths-pdf.fr/latex-images/0a141bd6fcd3d467230eb56d6a8ce513.png)
![]\frac{1}{2};+\infty[](https://maths-pdf.fr/latex-images/9a56ccbe1d9986e6be7ac20bbb073731.png)

5) Tracé de l’allure de 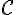
Utiliser les asymptotes et le tableau de variation pour tracer la courbe.
Exercice 2 – sens de variation, signe et solutions de l’inéquation.
1) Montrer que, pour tout 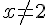
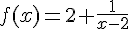
On a 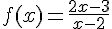
Il s’agit de séparer la fraction ainsi :
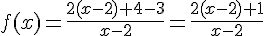
En divisant, on obtient :
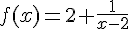
2) Donner les limites aux bornes de 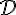
Quand x tend vers 2 par la gauche, 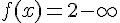
Quand x tend vers 2 par la droite, 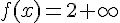
Quand x tend vers 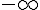
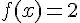
Quand x tend vers 
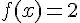
3) En utilisant la forme la plus adaptée, déterminer :
a) Le sens de variation de la fonction f :
La fonction 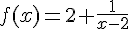
![]-\infty,2[](https://maths-pdf.fr/latex-images/40ecc79751042b27b6d4973ac5a88683.png)
![]2,+\infty[](https://maths-pdf.fr/latex-images/c378ed091c18b633281a211ee32077ab.png)
b) Le signe de f(x) :
Pour 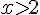
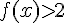
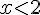
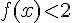
c) Les solutions de l’inéquation 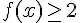
Il s’agit de résoudre 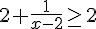
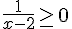
Donc 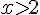
Les solutions sont donc ![]2,+\infty[](https://maths-pdf.fr/latex-images/c378ed091c18b633281a211ee32077ab.png)
Exercice 3 – préciser si les affirmations sont vraies ou fausses.
1) Réponse : Faux.
Si 
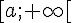
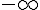
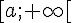
2) Réponse : Vrai.
Si 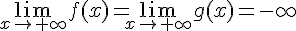
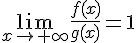
par définition du quotient de deux fonctions ayant la même limite infinie.
3) Réponse : Faux.
Pour 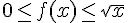
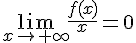
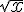

4) Réponse : Vrai.
La droite 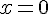
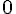
C’est le cas pour une fonction définie sur 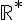
Exercice 4 – trouver la bonne réponse parmi les réponses proposées.
L’équation de la fonction est :
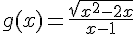
Il faut d’abord simplifier et analyser cette fonction. Le numérateur 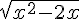
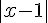
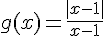
On a donc :
– Si 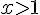
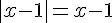
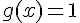
– Si 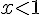
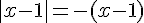
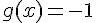
Pour le point 
Pour 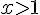
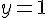
Pour 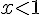
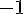
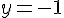
Conclusion : Les réponses correctes sont :
a et d
Exercice 5 – lien entre continuité et dérivabilité.
a) Si 



C’est vrai. En effet, la dérivabilité de 

du taux d’accroissement 
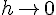
ce qui implique que 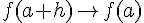
Donc, 

b) Si 



C’est faux. La continuité n’entraîne pas nécessairement la dérivabilité.
Un contre-exemple classique est la fonction valeur absolue 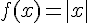
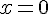
c) Si 

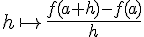
C’est vrai. Par définition même de la dérivabilité, si 


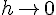
Cette limite est, en fait, 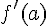
Exercice 6 – le théorème des gendarmes.
1) Réponse : On dit que f admet une limite finie 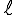

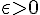
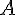
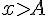
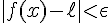
2) Démonstration du théorème des gendarmes :
Étant donné trois fonctions f, g, et h définies sur 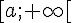
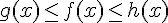

Si 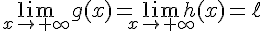


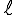
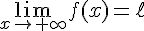
Exercice 7 – continuité en 1 et – 1 d’une fonction.
Première fonction :
Pour déterminer si la fonction est continue en 1, nous devons vérifier :
– La valeur de la fonction en 1 : 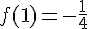
– La limite de la fonction lorsque x tend vers 1 :
Calculons 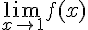
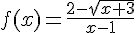
En appliquant le calcul de limite, nous avons :
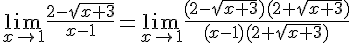
Ce qui se simplifie en :
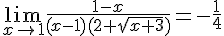
Puisque la limite est égale à la valeur de la fonction en 1, la fonction est continue en 1.
Deuxième fonction :
Pour déterminer si la fonction est continue en -1, nous devons vérifier :
– La valeur de la fonction en -1 : 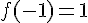
– La limite de la fonction lorsque x tend vers -1 :
Calculons 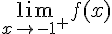

Lorsque x tend vers -1 par la droite :
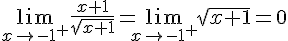
La limite n’étant pas égale à la valeur de la fonction en -1, la fonction n’est pas continue en -1.
Exercice 8 – déterminer les intervalles où f est continue.
Figure a :
1) Continuité : La fonction est continue sur ![]-1,1]\cup]1,2]](https://maths-pdf.fr/latex-images/d9f43ab7762ba71b1adbc3c603ea8b9b.png)
2) Image de 1 : 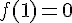
Les limites à gauche et à droite de 1 sont égales à 1, donc ne coïncide pas avec f(1).
Figure b :
1) Continuité : La fonction est continue sur ![]-1,1[\cup]1,2]](https://maths-pdf.fr/latex-images/c9bc561991702db25346ce9ee3fc43bf.png)
2) Image de 1 : 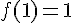
Les limites à gauche et à droite de 1 sont égales à 1, donc coïncide avec f(1).
Figure c :
1) Continuité : La fonction est continue sur ![]-1,1[\cup[1,2]](https://maths-pdf.fr/latex-images/49d12cc350dbb493170d9a6e61eae89c.png)
2) Image de 1 : 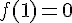
Les limites à gauche et à droite de 1 sont de 0 et 1 respectivement, donc ne coïncide pas avec f(1).
Figure d :
1) Continuité : La fonction est continue sur ![]-1,2]](https://maths-pdf.fr/latex-images/e320e1f8cffcf901e9ff29953f0d5981.png)
2) Image de 1 : 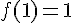
Les limites à gauche et à droite de 1 sont égales à 1, donc coïncide avec f(1).
Exercice 9 – déterminer l’ensemble de définition de f.
1) Déterminer l’ensemble de définition 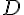

L’expression de la fonction est donnée par :
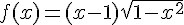
Pour que 
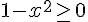
Cela équivaut à :
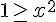
Ce qui donne :
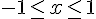
Donc, l’ensemble de définition 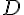
![D=\left[-1,1\right]](https://maths-pdf.fr/latex-images/db109b4bf2105c19f319f1ad29d167ac.png)
2) Représenter graphiquement 
Pour tracer la courbe de 
3) Étudier la continuité de 
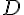
La fonction 
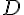
Exercice 10 – La fonction f est-elle continue en 1 ?.
1) Tracer la courbe représentative de f :
La fonction 
– 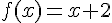
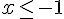
– 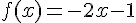

Tracez chaque partie de la fonction pour les valeurs données.
2) La fonction f est-elle continue en 1 ?
Pour qu’une fonction soit continue en un point, la limite à gauche et la limite à droite en ce point doivent être égales et la fonction doit être définie en ce point.
Calculons les limites à gauche et à droite en 
3) Déterminer 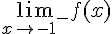
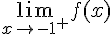
Pour 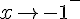
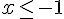
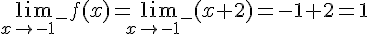
Pour 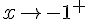

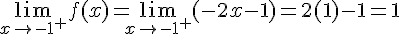
Conclusion : Comme les limites à gauche et à droite en 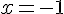

Télécharger ou imprimer cette fiche «la continuité : corrigé des exercices de maths en terminale en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.





