Loi à densité : corrigé des exercices de maths en terminale en PDF
Mis à jour le 25 novembre 2025
Dans cet article, nous aborderons la loi à densité, un concept clé en mathématiques pour les élèves de terminale. Comprendre cette notion est essentiel pour maîtriser les notions de probabilités et de statistiques, compétences fondamentales pour les épreuves du baccalauréat. À travers des exercices corrigés, les étudiants pourront renforcer leur savoir-faire en analyse et interprétation de données, garantissant ainsi leur succès dans cette discipline cruciale.
Exercice 1 – variable aléatoire modélisant une trotteuse.
1) Loi de la variable aléatoire :
La variable aléatoire modélisant la valeur donnée par la trotteuse est uniformément continue sur l’intervalle [0; 60] secondes. Elle suit donc une loi uniforme sur cet intervalle.
2) Probabilité de répondre de manière affirmative :
Paul répond par l’affirmative si la trotteuse indique entre 45 et 60 secondes, soit sur un intervalle de 15 secondes. La probabilité qu’un temps aléatoire soit compris dans cet intervalle est donnée par le rapport de la longueur de cet intervalle sur la longueur totale de 60 secondes :
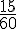
En simplifiant, on obtient :
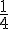
Donc, la probabilité que Paul réponde de manière affirmative est 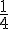
Exercice 2 – loi de densité d’une loi uniforme.
1) Pour la loi uniforme sur ![[-1;1]](https://maths-pdf.fr/latex-images/edb5e4bde1689863ffbe131d9af17a30.png)
La fonction de densité est donnée par :
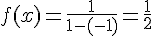
2) Pour la loi uniforme sur ![[0;120]](https://maths-pdf.fr/latex-images/86472a4bf5c724a94db6f18f02f6f69f.png)
La fonction de densité est donnée par :
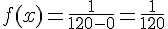
3) Pour la loi uniforme sur ![[-10;20]](https://maths-pdf.fr/latex-images/d071212fff9b76d0852056b7ebacc0e9.png)
La fonction de densité est donnée par :
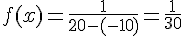
4) Pour la loi uniforme sur ![[-0,1;0,3]](https://maths-pdf.fr/latex-images/9524a25c8e4746e445af2012a056e86c.png)
La fonction de densité est donnée par :
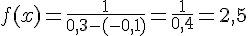
Exercice 3 – variable aléatoire suivant une loi exponentielle.
1) Calcul de P(Y < 1 500)
Pour une variable exponentielle de paramètre 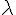
Donc, 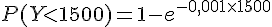
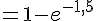
2) Calcul de P(400 ≤ Y ≤ 2 000)
On utilise la formule :
Donc,

3) Calcul de P(Y ≥ 1 000)
On sait que :
Donc, 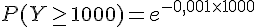
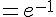
4) Calcul de P_{Y>1000}(Y>2000)
Il s’agit d’une probabilité conditionnelle :
On a déjà calculé 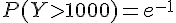
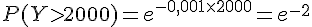
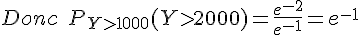
Exercice 4 – calculer une espérance.
1) Déterminer la valeur de 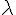
La densité d’une loi exponentielle est donnée par la formule :
On sait que 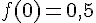
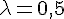
2) Que vaut 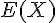
L’espérance 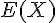
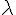

Avec 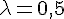
Exercice 5 – une variable aléatoire qui suit une loi exponentielle.
1) Déterminer 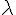
On sait que la probabilité que la variable aléatoire 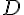
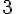
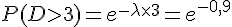
En comparant les exposants, on obtient :
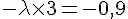
En résolvant cette équation, nous trouvons :
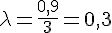
2) Calculer 
La probabilité que 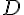
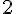
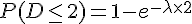
Avec 
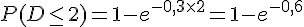
En calculant l’expression, nous trouvons :

Exercice 6 – déterminer les probabilités suivantes.
1) P(8 < X < 9) : La probabilité que X soit entre 8 et 9 est donnée sur le graphe : 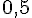
2) P(X ≥ 9) : Puisque la distribution est symétrique, la probabilité qu’X soit supérieur ou égal à 9 est : 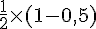
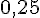
3) P(X ≤ 9) : La probabilité que X soit inférieur ou égal à 9 est l’ensemble de la distribution à gauche de 9 : 
4) P(X > 7)(X ≤ 8) : C’est la probabilité que X soit exactement entre 7 et 8, et cela est symétrique à P(8 < X < 9) : 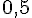
Exercice 7 – calculer la valeur des différentes probabilités.
1)
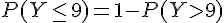
À partir de l’énoncé, on sait que 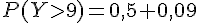
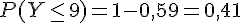
2)
Utilisons le schéma : 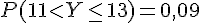
3)
Comme indiqué précédemment, 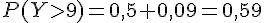
4)
Calculons 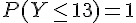
On trouve 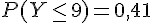
Donc,
Exercice 8 – déterminer une valeur approchée.
Dans une distribution normale, environ 95,4% des valeurs se trouvent dans l’intervalle ![[\mu-2\sigma,\mu+2\sigma]](https://maths-pdf.fr/latex-images/81067b242a88007d05006695480fb4e2.png)
La moyenne 
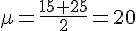
Pour trouver l’écart type 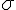
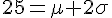
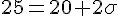
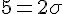
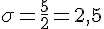
Exercice 9 – déduire des probabilités sans la calculatrice.
1) Déterminer une valeur approchée de 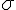
On a :
La probabilité 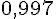
Donc : 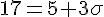
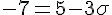
En résolvant l’une de ces équations : 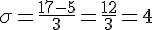
2) Calculer les probabilités suivantes sans utiliser de calculatrice.
a)
On cherche l’écart en nombre d’écarts-types :
– ![[-7\leq\, X\leq\, 17]](https://maths-pdf.fr/latex-images/9495e51f169969a90ce6a3bc537697b8.png)

– L’intervalle ![[1;9]](https://maths-pdf.fr/latex-images/ca8a88f36eb6aaeeaffe7fc708ddc849.png)
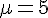
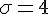
Donc :
b)
Intervalle de 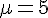
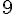

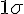
Donc :
Exercice 10 – calculer des probabilités sans calculatrice.
1) Calcul de P(1 ≤ X ≤ 3) :
Nous avons que 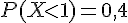
La loi normale est symétrique par rapport à la moyenne 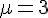
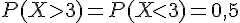
Ainsi,
2) Calcul de P(X>5) :
La probabilité 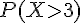
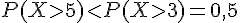
3) Calcul de P(X<5 | X≥1) :
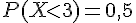
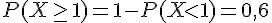
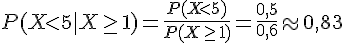
Télécharger ou imprimer cette fiche «loi à densité : corrigé des exercices de maths en terminale en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.












![[\mu - 3\sigma ; \mu + 3\sigma]](https://maths-pdf.fr/latex-images/99a36d230b1bb189fc7876b35d0419af.png)










