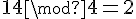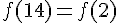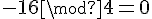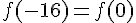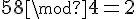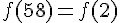Fonctions sinus et cosinus : corrigé des exercices de maths en terminale en PDF

Mis à jour le 25 novembre 2025

Les fonctions sinus et cosinus sont des notions clés en mathématiques, indispensables pour les élèves de terminale. Maîtriser ces fonctions permet de développer des compétences essentielles telles que l’analyse de graphiques, la résolution d’équations trigonométriques et l’application de concepts en physique. Dans cet article, nous vous proposons des corrections d’exercices pour vous aider à consolider vos connaissances et à exceller dans cette discipline cruciale.

Exercice 1 – f dérivable et tableau de variation.

1) Démontrer la limite :

Pour montrer que les limites sont $+\infty$ , on considère le comportement du numérateur et du dénominateur lorsque tend vers $+\infty$ et $-\infty$ .

Quand $x \to +\infty$ :

Le numérateur $x^2 + 2x + 5$ se comporte comme , et le dénominateur $\sqrt{x^2 + 1}$ se comporte aussi comme . Donc :

$f(x) = \frac{x^2 + 2x + 5}{\sqrt{x^2 + 1}} \sim \frac{x^2}{x} = x \to +\infty$

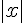
Similairement, quand $x \to -\infty$ , le comportement est identique :

$f(x) = \frac{x^2 + 2x + 5}{\sqrt{x^2 + 1}} \sim \frac{x^2}{|x|} = -x \to +\infty$

Donc, $\lim_{x \to \pm \infty} f(x) = +\infty$ .

2) Dérivabilité de :

La fonction $f(x) = \frac{x^2 + 2x + 5}{\sqrt{x^2 + 1}}$ est dérivable sur $\mathbb{R}$ par composition et division de fonctions dérivables.

La dérivée de est :

$f'(x) = \frac{(x - 1)(x^2 + x - 2)}{(x^2 + 1)\sqrt{x^2 + 1}}$

3) Tableau de variation :

Analysons les variations de à l’aide de :

– Les racines de fournissent les points critiques.

– Posons $g(x) = (x - 1)(x^2 + x - 2)$ . Les racines de $g(x) = 0$ sont obtenues par :

$(x - 1) = 0 \quad \Rightarrow \quad x = 1$

$x^2 + x - 2 = 0 \quad \Rightarrow \quad x = -2, \, x = 1$

(puisque $x = 1$ est déjà trouvé)

Évaluation des signes via :

$x < -2$ : \ négatif.
$-2 < x < 1$ : \ positif.
$x > 1$ : \ positif.

Conclusion : décroît sur $(-\infty, -2)$ , croît sur $(-2, 1)$ et $(1, +\infty)$ .

Exercice 2 – déterminer les limites suivantes.

1) Réponse : Nous utilisons la règle de l’Hôpital en raison de la forme indéterminée $\frac{0}{0}$ .

$\lim_{x\to\frac{\pi}{2}} \frac{\cos x}{(x-\frac{\pi}{2})\sin x}= \lim_{x\to\frac{\pi}{2}} \frac{-\sin x}{\sin x + (x-\frac{\pi}{2})\cos x} = \lim_{x\to\frac{\pi}{2}} \frac{-\sin x}{\sin x} = -1$

2) Réponse : Utilisons la limite remarquable $\lim_{x \to 0} \frac{\sin x}{x} = 1$ .

$\lim_{x\to 0} \frac{\sin(ax)}{\sin x} = \lim_{x\to 0} \frac{a \sin(x)}{ \sin x} = a$

3) Réponse : Appliquons la règle de l’Hôpital.

$\lim_{x\to 0} \frac{\cos x - 1}{\sin^2 x} = \lim_{x\to 0} \frac{-\sin x}{2\sin x \cos x} = \lim_{x\to 0} \frac{-1}{2\cos x} = 0$

4) Réponse : Utilisons l’identité $\cos^2 x - 1 = -\sin^2 x$ et simplifions.

$\lim_{x\to 0} \frac{\cos^2 x - 1}{x} = \lim_{x\to 0} \frac{-\sin^2 x}{x} = \lim_{x\to 0} \frac{-x^2}{x} = 0$

Exercice 3 – résoudre les équations.

1) Résoudre :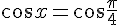

$x=\frac{\pi}{4}\text{ ou }x=-\frac{\pi}{4}$

2) Résoudre : 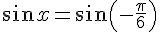$\sin{x}=\sin{(-\frac{\pi}{6})}$

$x=-\frac{\pi}{6}\text{ ou }x=\frac{7\pi}{6}$

3) Résoudre : 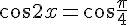$\cos{2x}=\cos{\frac{\pi}{4}}$

$2x=\frac{\pi}{4}\text{ ou }2x=-\frac{\pi}{4}$

Ce qui donne : $x=\frac{\pi}{8}\text{ ou }x=-\frac{\pi}{8}$

4) Résoudre : 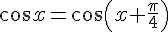$\cos{x}=\cos{(x+\frac{\pi}{4})}$

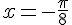
$x=-\frac{\pi}{8}$

5) Résoudre : 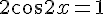$2\cos{2x}=1$

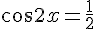
$\cos{2x}=\frac{1}{2}$

Donc : $2x=\frac{\pi}{3}\text{ ou }2x=-\frac{\pi}{3}$

Ce qui donne : $x=\frac{\pi}{6}\text{ ou }x=-\frac{\pi}{6}$

6) Résoudre : 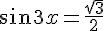$\sin{3x}=\frac{\sqrt{3}}{2}$

$3x=\frac{\pi}{3}\text{ ou }3x=\frac{2\pi}{3}$

Ce qui donne : $x=\frac{\pi}{9}\text{ ou }x=\frac{2\pi}{9}$

7) Résoudre : 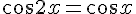$\cos{2x}=\cos{x}$

$2x=x+2k\pi\text{ ou }2x=-x+2k\pi$

Ce qui donne : $x=0\text{ ou }x=\frac{2k\pi}{3}$

8) Résoudre : 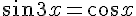$\sin{3x}=\cos{x}$

$3x=\frac{\pi}{2}-x+2k\pi\text{ ou }3x=-\frac{\pi}{2}+x+2k\pi$

Ce qui donne une solution complexe nécessitant plus de calculs pour chaque cas.

Exercice 4 – une étude de la dérivabilité de la fonction cosinus.

Commençons par réécrire la fonction :

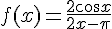
$f(x)=\frac{2\cos{x}}{2x-\pi}$

Nous voulons déterminer la limite de lorsque $x\to\frac{\pi}{2}$ .

Remarquons que nous avons une forme indéterminée $\frac{0}{0}$ à première vue. Nous allons donc utiliser la formule de Taylor pour le cosinus :

$\cos{x}=\cos{\frac{\pi}{2}}-\sin{\frac{\pi}{2}}(x-\frac{\pi}{2})+\frac{\cos{\frac{\pi}{2}}}{2}(x-\frac{\pi}{2})^{2}+\l\dots$

Ce qui simplifie à :

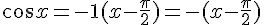
$\cos{x}=-1(x-\frac{\pi}{2})=-(x-\frac{\pi}{2})$

Ensuite, nous remplaçons dans l’expression de :

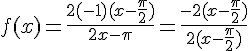
$f(x)=\frac{2(-1)(x-\frac{\pi}{2})}{2x-\pi}=\frac{-2(x-\frac{\pi}{2})}{2(x-\frac{\pi}{2})}$

Simplifions :

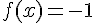
La limite est donc :

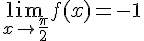
$\lim_{x\to\frac{\pi}{2}}f(x)=-1$

Exercice 5 – fonction homographique et polynôme.

1) Fonction affine :

Une fonction affine $x \mapsto ax + b$ est :

– Paire : Jamais.

– Impaire : Si et seulement si $b = 0$ .

2) Polynôme du second degré :

Une fonction polynomiale de degré 2 $x \mapsto ax^2 + bx + c$ est :

– Paire : Si et seulement si $b = 0$ .

– Impaire : Jamais (car le terme de degré 2 ne permet pas l’imparité).

3) Fonction homographique :

Une fonction homographique $x \mapsto \frac{ax + b}{cx + d}$ est :

– Paire : Si et seulement si $b = 0$ et $d = 0$ .

– Impaire : Si et seulement si $a = 0$ et $c = 0$ .

4) Polynôme du troisième degré :

Une fonction polynomiale de degré 3 $x \mapsto ax^3 + bx^2 + cx + d$ est :

– Paire : Jamais (car la présence de termes impairs empêche la parité).

– Impaire : Si et seulement si $b = 0$ et $d = 0$ .

Exercice 6 – exprimer les nombres en fonction de cosx et sinx.

1.a) $\sin(3\pi+x)=-\sin(x)$

1.b) $\cos(\frac{5\pi}{2}-x)=\sin(x)$

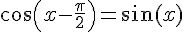
1.c) $\cos(x-\frac{\pi}{2})=\sin(x)$

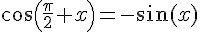
1.d) $\cos(\frac{\pi}{2}+x)=-\sin(x)$

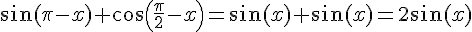
2.a) $\sin(\pi-x)+\cos(\frac{\pi}{2}-x)=\sin(x)+\sin(x)=2\sin(x)$

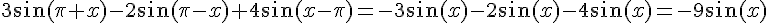
2.b) $3\sin(\pi+x)-2\sin(\pi-x)+4\sin(x-\pi)=-3\sin(x)-2\sin(x)-4\sin(x)=-9\sin(x)$

Exercice 7 – simplifier les cos et sin suivants.

1) Simplification de 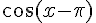$\cos(x-\pi)$ :

$-\cos(x)$

2) Simplification de 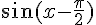$\sin(x-\frac{\pi}{2})$ :

$-\cos(x)$

3) Simplification de 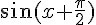$\sin(x+\frac{\pi}{2})$ :

$\cos(x)$

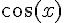
4) Simplification de 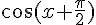$\cos(x+\frac{\pi}{2})$ :

$-\sin(x)$

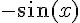
Exercice 8 – déterminer la valeur de cosinus et sinus.

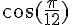
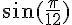
1) Calcul de $\cos(\frac{\pi}{12})$ et $\sin(\frac{\pi}{12})$

On utilise l’identité $\frac{\pi}{12} = \frac{\pi}{3} - \frac{\pi}{4}$ .

Formule de différence :

$\cos(a - b) = \cos a \cos b + \sin a \sin b$

Appliquons-la pour $a = \frac{\pi}{3}$ et $b = \frac{\pi}{4}$ :

$\cos(\frac{\pi}{12}) = \cos(\frac{\pi}{3} - \frac{\pi}{4}) = \cos(\frac{\pi}{3})\cos(\frac{\pi}{4}) + \sin(\frac{\pi}{3})\sin(\frac{\pi}{4})$

Valeurs connues :
$\cos(\frac{\pi}{3}) = \frac{1}{2}$ , $\sin(\frac{\pi}{3}) = \frac{\sqrt{3}}{2}$ , $\cos(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}$ , $\sin(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}$

$\cos(\frac{\pi}{12}) = (\frac{1}{2})(\frac{\sqrt{2}}{2}) + (\frac{\sqrt{3}}{2})(\frac{\sqrt{2}}{2})$

$= \frac{\sqrt{2}}{4} + \frac{\sqrt{6}}{4} = \frac{\sqrt{2} + \sqrt{6}}{4}$

Formule de différence pour le sinus :

$\sin(a - b) = \sin a \cos b - \cos a \sin b$

Appliquons-la pour 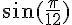$\sin(\frac{\pi}{12})$ :

$\sin(\frac{\pi}{12}) = \sin(\frac{\pi}{3} - \frac{\pi}{4}) = \sin(\frac{\pi}{3})\cos(\frac{\pi}{4}) - \cos(\frac{\pi}{3})\sin(\frac{\pi}{4})$

$= (\frac{\sqrt{3}}{2})(\frac{\sqrt{2}}{2}) - (\frac{1}{2})(\frac{\sqrt{2}}{2})$

$= \frac{\sqrt{6}}{4} - \frac{\sqrt{2}}{4} = \frac{\sqrt{6} - \sqrt{2}}{4}$

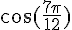
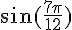
2) Calcul de $\cos(\frac{7\pi}{12})$ et $\sin(\frac{7\pi}{12})$

Utilisons l’identité $\frac{7\pi}{12} = \frac{\pi}{3} + \frac{\pi}{4}$ .

Formule de somme pour le cosinus :

$\cos(a + b) = \cos a \cos b - \sin a \sin b$

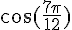
Appliquons-la pour $\cos(\frac{7\pi}{12})$ :

$\cos(\frac{7\pi}{12}) = \cos(\frac{\pi}{3} + \frac{\pi}{4}) = \cos(\frac{\pi}{3})\cos(\frac{\pi}{4}) - \sin(\frac{\pi}{3})\sin(\frac{\pi}{4})$

$= (\frac{1}{2})(\frac{\sqrt{2}}{2}) - (\frac{\sqrt{3}}{2})(\frac{\sqrt{2}}{2})$

$= \frac{\sqrt{2}}{4} - \frac{\sqrt{6}}{4} = -\frac{\sqrt{6} - \sqrt{2}}{4}$

Formule de somme pour le sinus :

$\sin(a + b) = \sin a \cos b + \cos a \sin b$

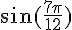
Appliquons-la pour $\sin(\frac{7\pi}{12})$ :

$\sin(\frac{7\pi}{12}) = \sin(\frac{\pi}{3} + \frac{\pi}{4}) = \sin(\frac{\pi}{3})\cos(\frac{\pi}{4}) + \cos(\frac{\pi}{3})\sin(\frac{\pi}{4})$

$= (\frac{\sqrt{3}}{2})(\frac{\sqrt{2}}{2}) + (\frac{1}{2})(\frac{\sqrt{2}}{2})$

$= \frac{\sqrt{6}}{4} + \frac{\sqrt{2}}{4} = \frac{\sqrt{6} + \sqrt{2}}{4}$

Exercice 9 – simplifier et résoudre des équations.

1) Simplifier l’expression suivante :

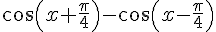
$\cos(x+\frac{\pi}{4})-\cos(x-\frac{\pi}{4})$

On utilise la formule de différence de cosinus : $\cos A-\cos B=-2\sin(\frac{A+B}{2})\sin(\frac{A-B}{2})$

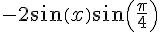
Donc, on a : $-2\sin(x)\sin(\frac{\pi}{4})$

Simplification : 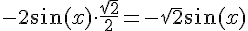$-2\sin(x)\times \frac{\sqrt{2}}{2}=-\sqrt{2}\sin(x)$

2) Établir l’égalité suivante :

$\frac{\sin 5x}{\sin 2x}+\frac{\sin 2x}{\sin x}=\frac{(\sin 3x)^2}{\sin 2x\sin x}$

Écrivons $\sin 5x$ et $\sin 3x$ avec les identités d’angle multiples :

$\sin 5x = \sin(2x + 3x) = \sin 2x \cos 3x + \cos 2x \sin 3x$

On simplifie chaque terme en développant avec les formules connues pour $\sin A\pm B$

Il reste à vérifier l’égalité par substitution et manipulation algébrique des termes.

3) Résoudre dans ]-π ; π] l’équation suivante :

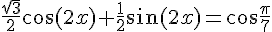
$\frac{\sqrt{3}}{2}\cos(2x)+\frac{1}{2}\sin(2x)=\cos\frac{\pi}{7}$

On exprime le membre de gauche comme un seul cosinus :

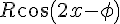
$R\cos(2x-\phi)$

où 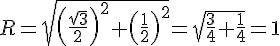$R=\sqrt{(\frac{\sqrt{3}}{2})^2+(\frac{1}{2})^2}=\sqrt{\frac{3}{4}+\frac{1}{4}}=1$

et $\tan\phi=\frac{1/2}{\sqrt{3}/2}=\frac{1}{\sqrt{3}}$

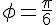
$\phi=\frac{\pi}{6}$

Donc, l’équation devient :

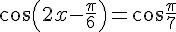
$\cos(2x-\frac{\pi}{6})=\cos\frac{\pi}{7}$

Ce qui donne les solutions :

$2x - \frac{\pi}{6} = \frac{\pi}{7} + 2k\pi \quad \text{ou} \quad 2x - \frac{\pi}{6} = - \frac{\pi}{7} + 2k\pi$

On résout pour dans chaque cas pour obtenir les valeurs entre et .

Exercice 10 – déterminer les coordonnées d’un vecteur.

1) a) Déterminer les coordonnées d’un vecteur $\vec{u}$ telles que $\mathcal{C}_f$ est invariante par translation de vecteur $\vec{u}$ .

Pour que la courbe soit invariante par translation, il faut que le vecteur $\vec{u}$ soit le vecteur période de la fonction. En analysant le graphique, on observe que la fonction recommence son motif toutes les 4 unités sur l’axe des abscisses.

Donc, un vecteur $\vec{u}$ qui traduit la fonction de la même manière est : $\vec{u}=(4\ ;\ 0)$

b) Déterminer la valeur de .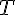

La période 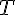de la fonction est donc de 4. Ainsi,

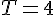
2) Donner l’image par des entiers : 14, -16, 56 et 58.

Étant donné que la fonction est périodique de période 4, on calcule chacune de ces valeurs modulo 4 pour trouver leur équivalent dans une période.

Pour 14 : $14\mod4=2$ donc
Pour -16 : $-16\mod4=0$ donc
Pour 56 : $56\mod4=0$ donc
Pour 58 : $58\mod4=2$ donc

Conclusion :

$f(14) = f(2)$
$f(-16) = f(0)$
$f(56) = f(0)$
$f(58) = f(2)$

En se référant au graphe, on lit :
$f(2) = 2$ et $f(0) = 0$ .

Donc, les images finales sont :
$f(14) = 2$ , $f(-16) = 0$ , $f(56) = 0$ , $f(58) = 2$ .

4.7/5 - (35017 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fonctions sinus et cosinus : corrigé des exercices de maths en terminale en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Limites de suites

Probabilités conditionnelles

Fonction exponentielle

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

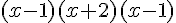
Maths PDF c'est 14 441 548 cours et exercices de maths téléchargés en PDF et 4 250 exercices.