Nombres complexes : corrigé des exercices de maths en terminale en PDF
Mis à jour le 25 novembre 2025
Exercice 1 – vérifier des égalités.
Calculons d’abord 
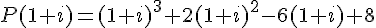
Calculons chaque terme :

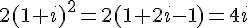
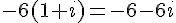
Donc :
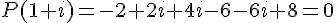
Ensuite, calculons 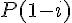
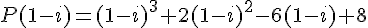
Calculons chaque terme :
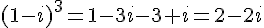
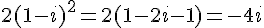

Donc :
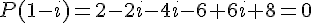
Conclusion : Nous avons vérifié que 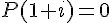
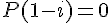
Exercice 2 – une fonction numérique et nombres complexes.
a) Calcul de 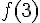
Substituons 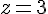
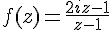

Donc, 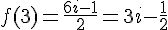
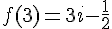
b) Calcul de 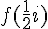
Substituons 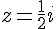
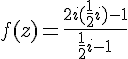

En multipliant le numérateur et le dénominateur par le conjugué du dénominateur :
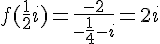
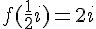
c) Calcul de 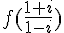
Simplifions d’abord 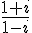
En multipliant le numérateur et le dénominateur par le conjugué du dénominateur :
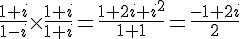
Alors, substituons 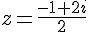
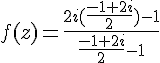
Calculons séparément :
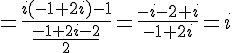
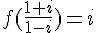
Exercice 3 – vérifier que les nombres sont des imaginaires purs.
Pour vérifier que 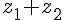
Calculons 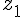

Multiplions le numérateur et le dénominateur par le conjugué de 
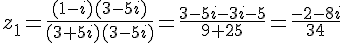
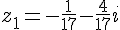
Calculons 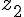
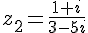
Multiplions le numérateur et le dénominateur par le conjugué de 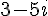


Somme :
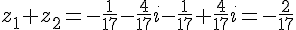
C’est donc un nombre réel.
Différence :
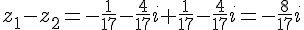
C’est donc un nombre imaginaire pur.
Exercice 4 – résoudre des équations dans C.
a) 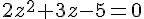
Les solutions sont obtenues en utilisant la formule quadratique.
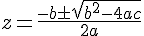
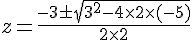
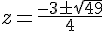
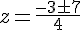
Solutions : 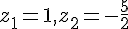
b) 
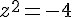
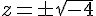
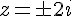
Solutions : 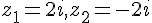
a) 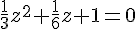
Multiplions par 6 pour simplifier :

Appliquons la formule quadratique :
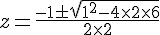
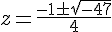
Solutions :
b) 
Appliquons la formule quadratique :
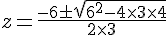
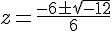
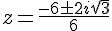
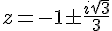
Solutions : 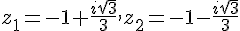
a) 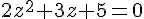
Utilisons la formule quadratique :

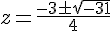
Solutions :
b) 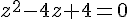
Ceci est un carré parfait :
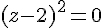
Solutions : 
a) 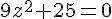
Simplifions :
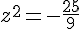
On a :
Solutions : 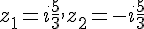
b) 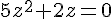
Factorisons :
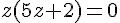
Solutions : 
Exercice 5 – résoudre l’équation avec des nombres complexes.
Pour résoudre l’équation 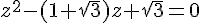
Calcul du discriminant 
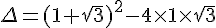
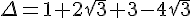
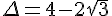
Les solutions sont données par la formule :
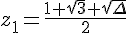
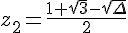
Donc les solutions de l’équation sont :
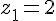
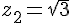
Exercice 6 – nombres complexes et trigonométrie.
Réponse pour a) 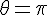
L’équation est 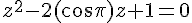
Calculons 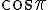
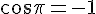
L’équation devient 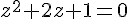
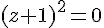
Donc, la solution est 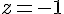
Réponse pour b) 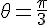
L’équation est 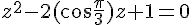
Calculons 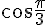
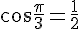
L’équation devient 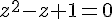
Le discriminant est 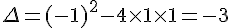
Les solutions sont donc :


Exercice 7 – résoudre dans C l’équation .
Pour résoudre l’équation 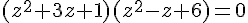
Étape 1 : Résolution de l’équation 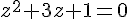
Les racines de cette équation sont données par la formule quadratique :
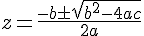
En substituant 
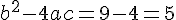
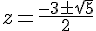
Étape 2 : Résolution de l’équation 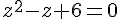
Les racines de cette équation sont données par la formule quadratique :
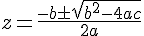
En substituant 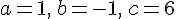

Les solutions sont alors complexes :
Conclusion : Les solutions de l’équation sont :

Exercice 8 – polynôme et résolution de l’équation.
a) Justification :
Pour factoriser le polynôme 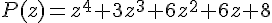
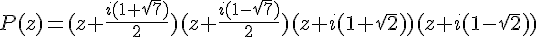
Les facteurs obtenus sont bien conformes à l’affichage. Chaque facteur correspond à une racine complexe du polynôme, obtenue par résolution d’équations quadratiques.
b) Résolution de l’équation :
Pour résoudre 
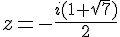
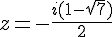
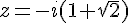
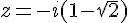
Donc, les solutions de l’équation 

Exercice 9 – systèmes d’équations avec des nombres complexes.
Nous devons résoudre le système d’équations suivant :
1. 
2. 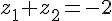
Considérons les équations sous forme de polynômes dont les racines sont 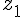
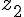
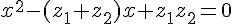
Cela donne :
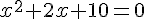
Utilisons la formule quadratique pour résoudre le polynôme :
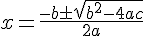
Dans cette équation, 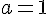
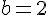
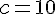
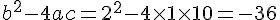
Comme le discriminant est négatif, les solutions sont complexes :
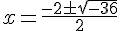
Les solutions sont donc :
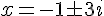
Donc, les nombres complexes recherchés sont :
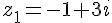
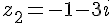
Exercice 10 – déterminer la forme algébrique.
1. Calcul de 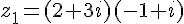
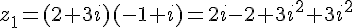

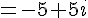
2. Calcul de 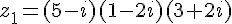
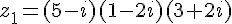
3. Calcul de 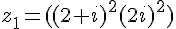
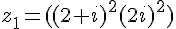
4. Calcul de 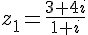
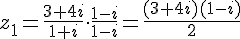

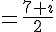
5. Calcul de 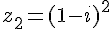
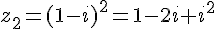
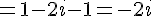
6. Calcul de 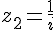
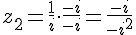
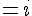
7. Calcul de 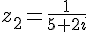
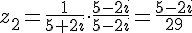
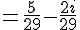
8. Calcul de 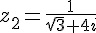
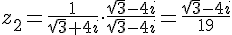
Télécharger ou imprimer cette fiche «nombres complexes : corrigé des exercices de maths en terminale en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.









