Problèmes et calculs : corrigé des exercices de maths en CM1 en PDF

Mis à jour le 23 novembre 2025

Les problèmes et calculs en mathématiques sont essentiels pour les élèves de CM1, car ils leur permettent de développer des compétences cruciales telles que la résolution de problèmes et le calcul mental. Ces exercices aident les enfants à apprendre à analyser des situations, à appliquer des stratégies et à renforcer leur compréhension des nombres et des opérations. Dans cet article, nous allons vous proposer des corrections d’exercices pratiques pour accompagner vos élèves dans leur apprentissage et maximiser leur réussite en mathématiques.

Exercice 1 – une mare rectangulaire.

1a. Le volume de terre retirée est de 6 m³. Sachant que la terre pèse 1,5 tonne par mètre cube :

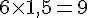
$6\times 1,5=9$ tonnes de terre.

1b. Si la remorque peut transporter jusqu’à 500 kg de terre :

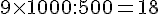
$9\times 1000:500=18$ chargements nécessaires.

1c. Si la remorque pouvait transporter 750 kg de terre :

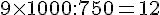
$9\times 1000:750=12$ chargements auraient été nécessaires, ce qui économise 6 voyages.

2a. La bâche a besoin d’une longueur pour recouvrir les bords de la mare.

C’est pourquoi elle mesure 42 m² (6 m de large par 7 m de long). Cela inclut les côtés pour tenir correctement autour de la mare.

2b. Sachant que le m² de bâche coûte 8 € :

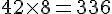
$42\times 8=336$ € pour 42 m².

3a. Les débits des pompes disponibles sont :

Première pompe : $\frac{4500}{60}=75$ L/min
Seconde pompe : $\frac{7500}{60}=125$ L/min

3b. Temps nécessaire pour remplir la mare avec chaque pompe :

Première pompe : $\frac{6000}{75}=80$ minutes
Seconde pompe : $\frac{6000}{125}=48$ minutes

Exercice 2 – la croissance du pogona.

a. Complète ce tableau en lisant son poids en fonction de son âge sur le graphique :

Âge en mois : 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24

Poids en g : 5, 65, 140, 185, 240, 280, 320, 380, 420, 450, 480, 500, 580

b. Tableau de taille : Voici le graphique où vous placez les points pour chaque âge selon la taille fournie :

Âge en mois : 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24

Taille en cm : 8, 18, 24, 31, 36, 41, 51, 56, 57, 58, 58, 59, 60

Exercice 3 – l’alimentation du pogona.

a. Combien mange-t-il de grillons au total, au cours de chacun des quatre premiers stades ?

Bébé : 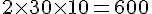$2\times 30\times 10=600$

Juvénile : 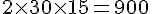$2\times 30\times 15=900$

Juvénile avancé : 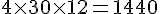$4\times 30\times 12=1440$

Sub adulte : 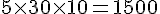$5\times 30\times 10=1500$

Total pour les quatre premiers stades :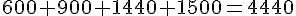

Adulte : 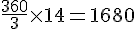$\frac{360}{3}\times 14=1680$

b. Combien de grillons mange un pogona âgé pendant un an ?

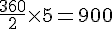
$\frac{360}{2}\times 5=900$

c. Combien de grillons mange un pogona au cours des trois premières années de sa vie ?

Total pour les quatre premiers stades : 4440

Adulte : 1680 (pour la première année adulte)

Âgé : 900 (pour la deuxième année adulte)

Trois premières années :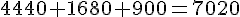

Exercice 4 – problème du spectacle.

a. Ils arrivent, en voiture, 34 minutes avant le début du spectacle. À quelle heure arrivent-ils ?

Le spectacle commence à 17 h 15. En arrivant 34 minutes avant, ils arrivent à :

17 h 15 – 34 min = 16 h 41.

b. Combien de temps dure le spectacle (avec l’entracte) ?

La durée totale du spectacle est la somme des deux périodes et de l’entracte :

55 min + 20 min + 50 min = 125 minutes.

c. À quelle heure quittent-ils la salle de spectacle ?

Le spectacle dure 125 minutes (2 heures et 5 minutes), donc ils quittent la salle à :

17 h 15 + 2 h 5 min = 19 h 20.

d. Ils se sont garés dans un parking souterrain à 2 € de l’heure (l’heure commencée est due). Combien paient-ils ?

Temps total passé au parking :

De 16 h 41 à 19 h 20 = 2 heures et 39 minutes, donc 3 heures sont dues.

Coût total : 3 x 2 € = 6 €.

Exercice 5 – problème de l’anniversaire.

a. Tableau des ingrédients pour 60 choux :

– Eau pour 60 choux : 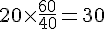$20\times \frac{60}{40}=30$ cL

– Beurre pour 60 choux : 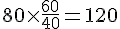$80\times \frac{60}{40}=120$ g

– Œufs pour 60 choux : 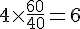$4\times \frac{60}{40}=6$

– Farine pour 60 choux : 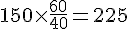$150\times \frac{60}{40}=225$ g

– Sel : 1 pincée

b. Choux dans la pyramide :

Il y a 5 niveaux dans la pyramide, chaque niveau a une base carré de côté 5, 4, 3, 2, 1. Donc le nombre total de choux est :

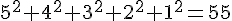
c. Choux pour cinq étages :

Comme déjà calculé, pour cinq étages, le total est :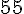

d. Choux pour un sixième étage :

Pour un sixième étage, la base carrée serait de côté 6 :

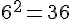
Donc, il lui faut 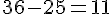choux supplémentaires.

Exercice 6 – problème du cocktail.

a. De quelle quantité de chaque jus de fruits a-t-il besoin ?

Il utilise 1/10 L de sirop de fraise pour 5 verres. Avec 1 L de sirop, il peut préparer :

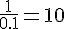
$\frac{1}{0.1}=10$

Il peut donc préparer 10 fois la quantité de 5 verres, soit 50 verres.

Pour 50 verres, il a besoin de :

40 cL de jus de pomme par 5 verres, donc $40\times 10=400$ cL de jus de pomme.
$0.25\times 10=2.5$ L de jus de poire.
$0.25\times 10=2.5$ L de jus d’abricot.
$0.1\times 10=1$ L de sirop de fraise (toute la bouteille).

b. Quelle est la quantité totale de cocktail préparé ?

Pour 50 verres :

Jus de pomme : 400 cL = L
Jus de poire : L
Jus d’abricot : L
Sirop de fraise : L

Quantité totale : 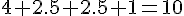L

c. Combien de verres peut-il servir ?

Zolan peut servir 50 verres avec 10 L de cocktail.

Exercice 7 – problème de la piscine.

a. Représentation des bassins :

Le premier bassin mesure 50 m x 20 m et le deuxième a des dimensions réduites de moitié, soit 25 m x 10 m.

b. Calcul des périmètres :

Premier bassin : 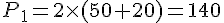$P_1=2\times (50+20)=140$ m

Deuxième bassin : 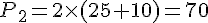$P_2=2\times (25+10)=70$ m

Rapport des périmètres : 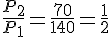$\frac{P_2}{P_1}=\frac{70}{140}=\frac{1}{2}$

c. Calcul des aires :

Premier bassin : 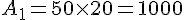$A_1=50\times 20=1000$ m²

Deuxième bassin : 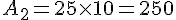$A_2=25\times 10=250$ m²

Rapport des aires : 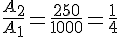$\frac{A_2}{A_1}=\frac{250}{1000}=\frac{1}{4}$

Exercice 8 – problème du bassin olympique.

a. Combien de baignoires de 125 L seraient nécessaires pour remplir ce bassin ?

La capacité du bassin est de 37 500 hL, ce qui équivaut à 3 750 000 L.

Nombre de baignoires nécessaires :
$\frac{3\ 750\ 000}{125}=30\ 000$

b. Et combien d’aquariums de 500 L ?

Nombre d’aquariums nécessaires :
$\frac{3\ 750\ 000}{500}=7\ 500$

c. Quelle est la capacité d’un bassin olympique de profondeur 2 m ?

La capacité est proportionnelle à la profondeur. Donc pour une profondeur de 2 m :
$\frac{2}{3} \times 37\ 500 = 25\ 000\ \text{hL}$

d. Reprends les questions a et b pour un bassin olympique profond de 2 m.

a. Nombre de baignoires nécessaires :
$\frac{2\ 500\ 000}{125}=20\ 000$

b. Nombre d’aquariums nécessaires :
$\frac{2\ 500\ 000}{500}=5\ 000$

Exercice 9 – problème du championnat de France.

Réponse a :

Classement pour 2014 :

1. Zoé – 27.45 s

2. Maëlle – 27.12 s

3. Mathilde – 27.24 s

4. Nolwenn – 27.53 s

5. Solveig – 27.50 s

6. Joana – 27.30 s

7. Alex – 27.59 s

8. Pauline – 27.37 s

Classement pour 2013 :

1. Emma – 26.88 s

2. Julia – 26.95 s

3. Claire – 27.51 s

4. Manon – 27.08 s

5. Meredith – 27.41 s

6. Morgane – 27.73 s

7. Julie – 27.58 s

8. Sandrine – 28.01 s

Réponse b :

Classement global sur les deux ans :

1. Emma – 26.88 s

2. Julia – 26.95 s

3. Maëlle – 27.12 s

4. Manon – 27.08 s

5. Mathilde – 27.24 s

6. Joana – 27.30 s

7. Pauline – 27.37 s

8. Meredith – 27.41 s

9. Zoé – 27.45 s

10. Claire – 27.51 s

11. Solveig – 27.50 s

12. Nolwenn – 27.53 s

13. Julie – 27.58 s

14. Alex – 27.59 s

15. Morgane – 27.73 s

16. Sandrine – 28.01 s

4.9/5 - (32075 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «problèmes et calculs : corrigé des exercices de maths en CM1 en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Les nombres décimaux

Les aires

Durée, longueur, masse et volume

Tableaux et graphiques

Les périmètres

Construction de figures

Proportionnalité

Les fractions

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

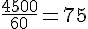
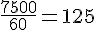
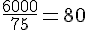
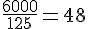
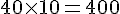
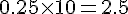
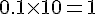
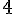
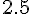
Maths PDF c'est 14 363 634 cours et exercices de maths téléchargés en PDF et 4 250 exercices.