Coordonnées et repérage dans le plan : cours de maths en 2de à imprimer en PDF.

Mis à jour le 14 mars 2025

Sommaire

📚Cours de MathématiquesSeconde • lycée

Coordonnées et repérage dans le plan

⏱️Temps de lecture : 3 min

🎯Difficulté : Avancé

📚Seconde générale

📋Prérequis : Brevet des collèges obtenu

📄Format PDF disponible gratuitement

Les vecteurs du plan et les coordonnées et le repérage à travers un cours de maths en 2de à télécharger en PDF. L’élève devra connaître la définition d’un vecteur et ses différentes caractéristiques. Ainsi que les différentes opérations sur les vecteurs (somme, produit par un nombre réel), savoir calculer les coordonnées ainsi que la valeur de sa norme en appliquant les formules de la leçon en seconde.

I. Définition et vocabulaire

On considère que le plan est muni d’un repère 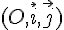$(O,\vec{i},\vec{j})$ .

Définition :

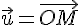
Soit $\vec{u}$ un vecteur du plan. On considère le point M(a,b) tel que $\vec{u}=\vec{OM}$ .

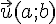
Les coordonnées du vecteur $\vec{u}$ sont celles du point M, nous avons $\vec{u}(a;b)$ .

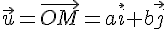
Nous avons $\vec{u}=\vec{OM}=a\vec{i}+b\vec{j}$ .

Propriété :

Deux vecteurs sont égaux si et seulement si ils ont les mêmes coordonnées.

II. Coordonnées et opérations sur les vecteurs

Propriété :

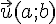
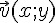
Soient deux vecteurs $\vec{u}(a;b)$ et $\vec{v}(x;y)$ et k un nombre réel. Les coordonnées du vecteur :

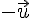
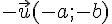
$-\vec{u}$ sont $-\vec{u}(-a;-b)$ ;

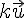
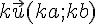
$k\vec{u}$ sont $k\vec{u}(ka;kb)$ ;

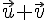
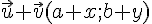
$\vec{u}+\vec{v}$ sont $\vec{u}+\vec{v}(a+x;b+y)$ ;

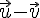
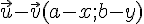
$\vec{u}-\vec{v}$ sont $\vec{u}-\vec{v}(a-x;b-y)$ .

III. Coordonnées de points et longueur

Propriété :

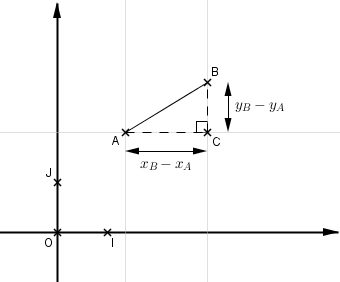
Soient A et B deux points du plan tels que 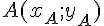et .

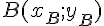
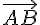
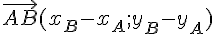
Le vecteur $\vec{AB}$ a pour coordonnées $\vec{AB}(x_B-x_A;y_B-y_A)$ .

Propriété :

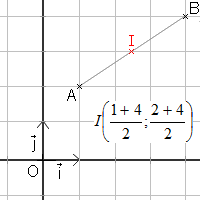
Soient A et B deux points du plan tels que 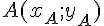et .Soit I le milieu du segment [AB].

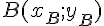
Le point I a pour coordonnées 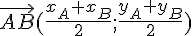$\vec{AB}(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2})$ .

Exemple :

Soit 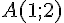et .

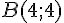
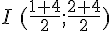
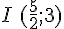
Le milieu I du segment [AB] a pour coordonnées $I\,(\frac{1+4}{2};\frac{2+4}{2})$ , soit $I\,(\frac{5}{2};3)$ .

Propriété :

Soient A et B deux points du plan tels que 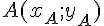et .

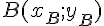
La longueur AB vaut 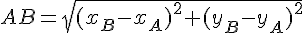$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$ (théorème de Pythagore).

Exemple :

Soit 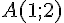et .

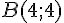
La longueur du segment [AB] est :

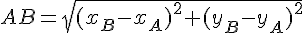
$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$

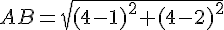
$AB=\sqrt{(4-1)^2+(4-2)^2}$

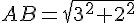
$AB=\sqrt{3^2+2^2}$

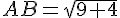
$AB=\sqrt{9+4}$

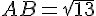
$AB=\sqrt{13}$

4.9/5 - (30349 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «coordonnées et repérage dans le plan : cours de maths en 2de à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Cours de Seconde

Résoudre des équations et inéquations

Fonction linéaire et affine

Calcul littéral, fractions, puissances, racines carrées

Fonction carrée, cube, racine carrée et inverse

Exercices de Seconde

Géométrie dans l’espace

Inéquations

Fonction inverse

Statistiques

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 13 812 143 cours et exercices de maths téléchargés en PDF et 4 250 exercices.