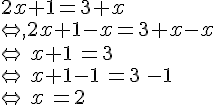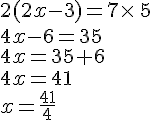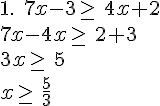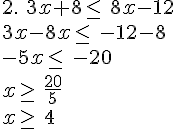Résoudre des équations et inéquations : cours de maths en 2de à imprimer en PDF.

Mis à jour le 29 mai 2025

Sommaire

📚Cours de MathématiquesSeconde • lycée

Résoudre des équations et inéquations

⏱️Temps de lecture : 4 min

🎯Difficulté : Avancé

📚Seconde générale

📋Prérequis : Brevet des collèges obtenu

📄Format PDF disponible gratuitement

Les équations et les inéquations du premier degré à une inconnue à travers un cours de maths en 2de à télécharger en PDF. L’élève devra connaître la définition d’une équation (premier et second membre, inconnue, ensemble solution) ainsi que pour une inéquation. Nous terminerons cette leçon par des applications issues de la vie courante similaires à celles de votre manuel scolaire en seconde.

I. Résoudre des équations :

Définition :

On considère deux expressions algébriques A(x) et B(x) dépendantes de la variable x qui prend ses valeurs dans un ensemble E.

Résoudre dans E l’équation A(x)=B(x) d’inconnue x, c’est déterminer l’ensemble des nombres x

dans E tels que l’égalité A(x)=B(x) soit vraie.

Cet ensemble est appelé l’ensemble solution de l’équation dans E.

A(x) est appelé le premier membre de l’équation et B(x) est appelé le second membre.

Définition :

Deux équations sont équivalentes si elles ont le même ensemble solution.

Exemple :

Considérons l’équation suivante :

$2x+1=3+x\\\Leftrightarrow,2x+1-x=3+x-x\\\Leftrightarrow\,x+1\,=3\,\\\Leftrightarrow\,x+1-1\,=3\,-1\\\Leftrightarrow\,x\,=2$

L’ensemble solution dans $\mathbb{R}$ de cette équation est S={2}.

Propriété : équation-produit.

Un produit de facteur est nul si et seulement si l’un des facteurs, au moins, est nul. $A_1(x)\times \,A_2(x)\times \,A_3(x)\times \,.....A_n(x)=0$

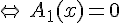
$\Leftrightarrow\,A_1(x)=0$ ou ou ou ……. ou .

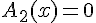
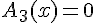
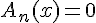
Exemple :

Résoudre l’équation-produit suivantes :

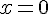
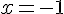
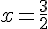
équivaut à ou ou $x=\frac{3}{2}$ .

Propriété :

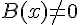
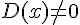
On considère des expressions algébriques A(x), B(x), C(x) et D(x) dépendantes de la variable avec $B(x)\neq0$ et $D(x)\neq0$ .Nous avons :

$\frac{A(x)}{B(x)}=0\Leftrightarrow\,A(x)=0$

$\frac{A(x)}{B(x)}=C(x)\Leftrightarrow\,A(x)=B(x)\times \,C(x)$

$\frac{A(x)}{B(x)}=\frac{C(x)}{D(x)}\Leftrightarrow\,A(x)\times \,D(x)=B(x)\times \,C(x)$

Exemple :

Résoudre l’équation suivante

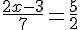
$\frac{2x-3}{7}=\frac{5}{2}$

$2(2x-3)=7\times \,5\\4x-6=35\\4x=35+6\\4x=41\\x=\frac{41}{4}$

II. Résoudre des inéquations :

Définition :

On considère deux expressions algébriques A(x) et B(x) dépendantes de la variable x qui prend ses valeurs dans un ensemble E.

Résoudre dans E l’inéquation A(x)<B(x) d’inconnue x, c’est déterminer l’ensemble des nombres x

dans E tels que l’inégalité A(x)<B(x) soit vraie.

Cet ensemble est appelé l’ensemble solution de l’inéquation dans E.

A(x) est appelé le premier membre de l’inéquation et B(x) est appelé le second membre.

Propriété :

Nous obtenons des inéquations équivalentes lorsque :On additionne un même nombre réels aux deux membres de l’inéquation;

On multiplie (ou divise) chaque membre de l’inéquation par un même nombre réel strictement positif;

On multiplie(ou divise), chaque membre de l’inéquation, par un même nombre réel strictement négatif et en changeant le sens de l’inégalité.

Exemple :

Pour tout nombre x :

$3x+1<2\Leftrightarrow\,3x+1-1<2-1\Leftrightarrow\,3x\,<1\Leftrightarrow\,\frac{3x}{3}\,<\frac{1}{3}\Leftrightarrow\,x<\frac{1}{3}$ .

Autre version de cette leçon

I. Les inéquations du premier degré à une inconnue

Définition :

Une inéquation est une inégalité entre deux expressions comportant des lettres appelées inconnues.

Exemples :

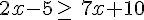
$2x-5\geq\,\,7x+10$

$2xy+7x+x\leq\,\,x^2-y^2+2xy+7x$

Définition :

Résoudre une inéquation d’inconnue x, c’est déterminer toutes les valeurs de x (si elles existent) pour lesquelles l’inégalité est vraie. Chacune de ces valeurs est appelée solution de l’inéquation.

II. résoudre une inéquation du premier degré

Propriétés :

On ne modifie pas le sens d’une inégalité lorsque l’on ajoute (ou soustrait) le même nombre à chaque membre de l’inéquation;
On ne modifie pas le sens d’une inégalité lorsque l’on multiplie (ou divise) chaque membre de l’inéquation par un nombre positif non nul.
On change le sens d’une inégalité lorsque l’on multiplie (ou divise) chaque membre de l’inéquation par un nombre négatif non nul.

Exemples :

Résoudre les inéquations suivantes :

$1.\,\,\,7x-3\geq\,\,4x+2\\7x-4x\geq\,\,2+3\\3x\geq\,\,5\\x\geq\,\,\frac{5}{3}$

$2.\,\,3x+8\leq\,\,8x-12\\3x-8x\leq\,\,-12-8\\-5x\leq\,\,-20\\x\geq\,\,\frac{20}{5}\\x\geq\,\,4$

III. Résolution de problèmes avec des inéquations

1.Sonia a eu 11 notes au cours du trimestre.

Sa moyenne est actuellement de 13,7 sur 20.

Quelle note doit-elle obtenir au minimum à son prochain devoir pour que sa moyenne devienne supérieure ou égal à 14 ?

2. Pour transporter des enseignes, une société souhaite comparer les tarifs de deux entreprises :

l’entreprise « Vitlivré » propose une somme de 3,20 € par kilomètre parcouru, tandis que l’entreprise « Rapido » propose un forfait de 180 € puis une somme de 2 € par kilomètre parcouru.

a.Quelle entreprise faut-il choisir pour un transport de 100 kilomètres ?

b.A partir de quel kilométrage l’entreprise « Rapido » est-elle la plus intéressante ?

4.7/5 - (34222 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «résoudre des équations et inéquations : cours de maths en 2de à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Cours de Seconde

Fonction linéaire et affine

Statistiques

Coordonnées et repérage dans le plan

Probabilités

Exercices de Seconde

resolution graphique equations inequations exercices maths 2de

Résolution graphique d’équations et inéquations

Inéquations

Géométrie dans l’espace

algorithmes programmes exercices maths 2de

Algorithmes et programmes

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 13 856 273 cours et exercices de maths téléchargés en PDF et 4 250 exercices.