L’étude graphique et algébrique des fonctions : cours de maths en 2de à imprimer en PDF.
Mis à jour le 20 décembre 2025
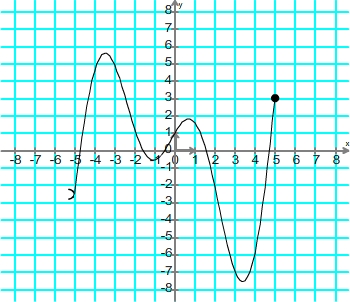
I. Représenter graphiquement une fonction
Dans un repère orthonormé du plan, une fonction f définie sur un ensemble 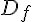
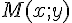
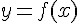
Cet ensemble de points est appelée la courbe représentative de la fonction f et l’ensemble 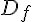
Exemple :
Soit la fonction f définie par 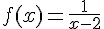
Une fraction est définie lorsque son dénominateur est non nul, par conséquent, 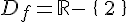
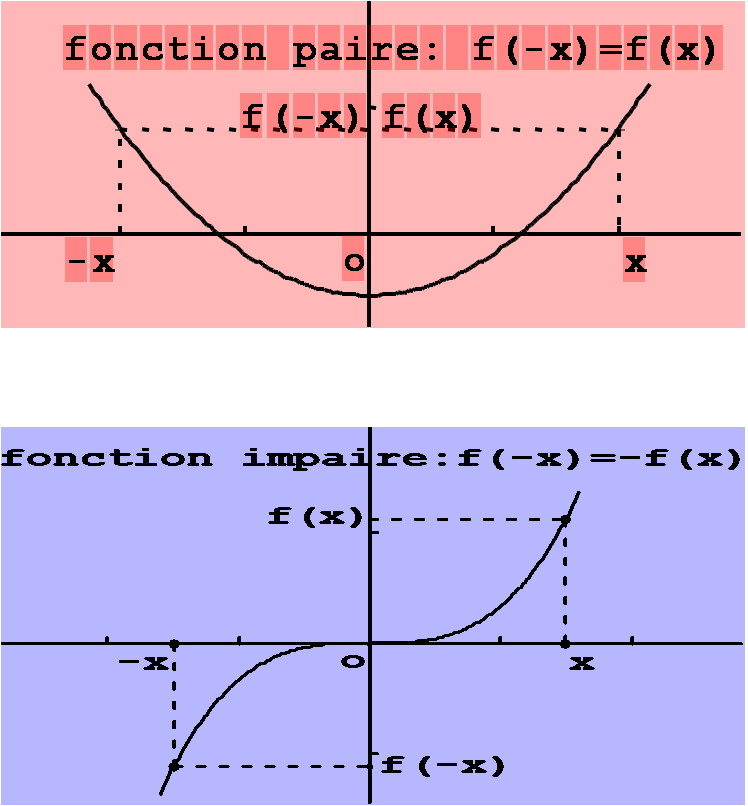
Soit f définie sur un ensemble 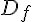
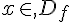
Si pour tout 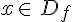
Exemple :
La fonction f définie par 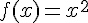
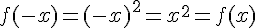
La fonction f définie par 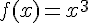
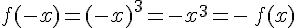
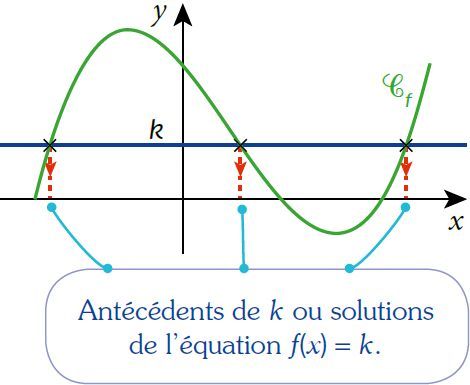
II. Résoudre graphiquement une équation
Résoudre graphiquement l’équation f(x)=k revient à déterminer les abscisses des points d’intersection des courbes y=f(x) et y=k.
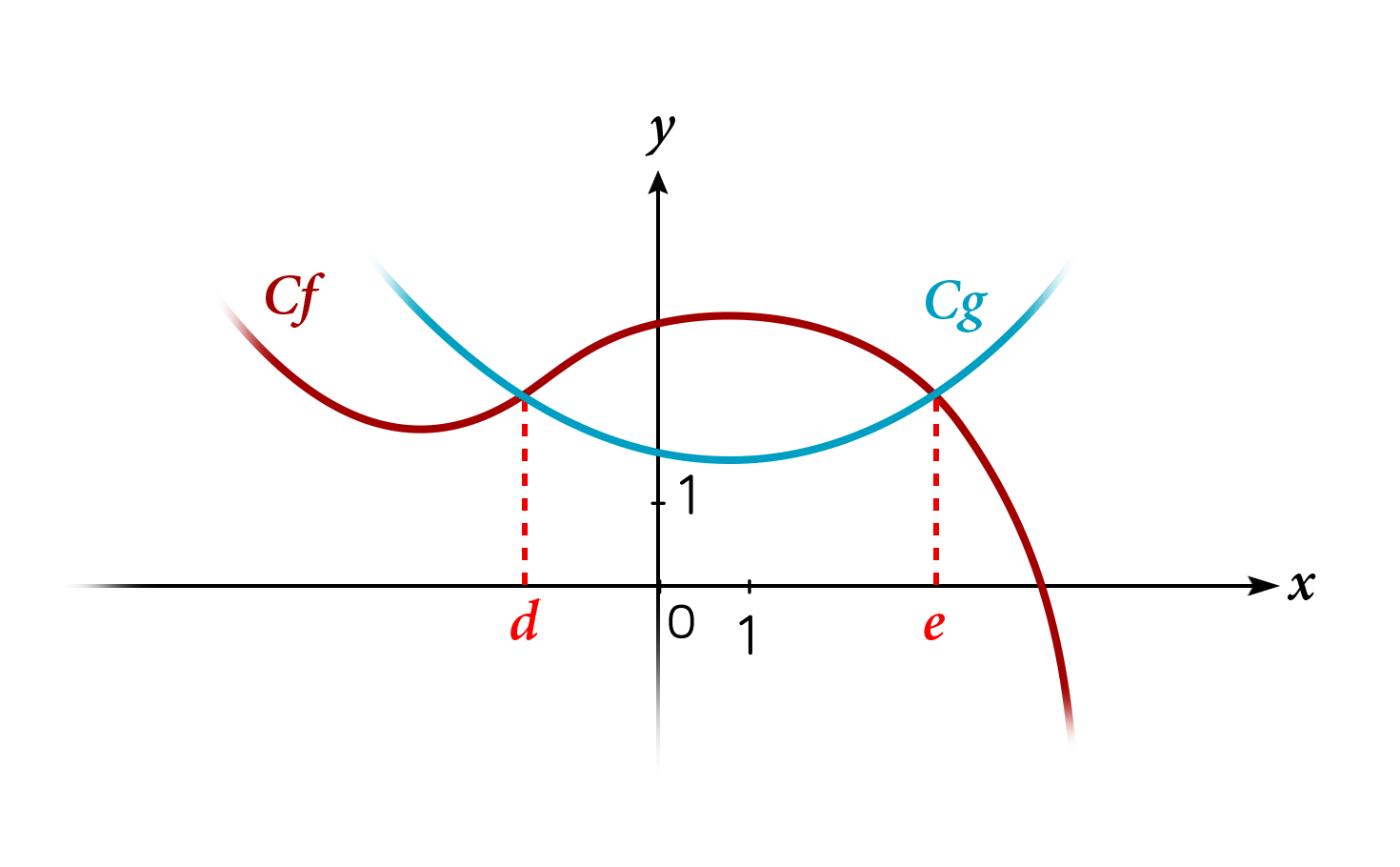
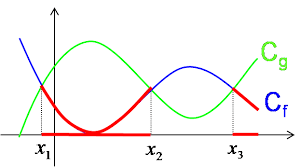
Résoudre graphiquement l’équation f(x)=g(x) revient à déterminer les abscisses des points d’intersection des courbes 
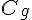
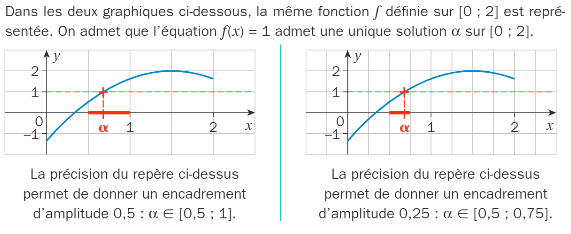
Soit f une fonction définie sur un ensemble 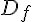
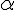
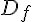
![\alpha\,\in\,[a;b]](https://maths-pdf.fr/latex-images/e416d8945140b70014dbef32857393a6.png)
C’est à dire que 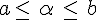
La précision de l’encadrement correspond à l’amplitude de l’intervalle [a ; b] et elle est de b-a.
III. Résoudre graphiquement une inéquation
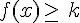

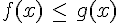
des points de

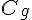
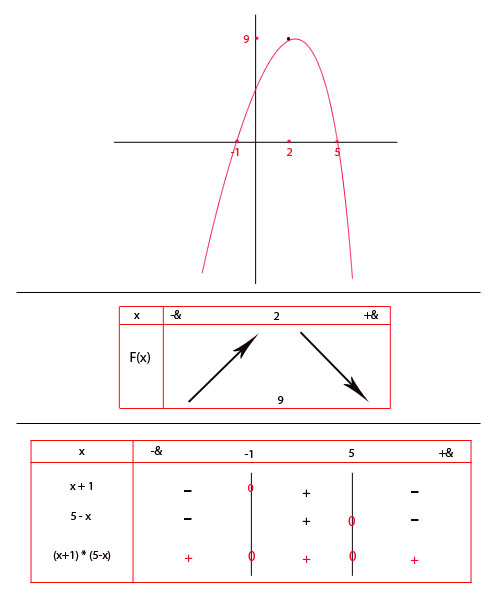
Dresser le tableau de signe d’une fonction f définie sur un ensemble 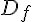

- Si
- Si
- Si
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «l'étude graphique et algébrique des fonctions : cours de maths en 2de à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de Seconde
Exercices de Seconde
Nos applications
Téléchargez la dernière version gratuite de nos applications.