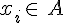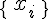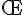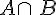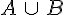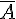Probabilités : cours de maths en 2de à imprimer en PDF.

Mis à jour le 16 mars 2025

Sommaire

Les probabilités à travers un cours de maths en 2de à télécharger en PDF. L’élève devra savoir ce qu’est une expérience aléatoire, un événement et une issue. Développer des compétences en modélisant une expérience aléatoire et en sachant calculer une probabilité en seconde.

I. Probabilité sur un ensemble fini

1.Expérience aléatoire

Définition :

Une expérience est dite aléatoire lorsqu’elle a plusieurs issues ( ou résultats) possibles et que l’on ne peut ni prévoir, ni calculer laquelle de ces issues sera réalisée. On dit que l’ensemble $E=\,\{x_1,x_2,x_3,....,x_n\,\}$ des issues possibles est l’univers de cette expérience aléatoire.

Exemple :

On lance un dé cubique dont les faces sont numérotées de 1 à 6 et on lit le numéro porté par la face supérieure.

L’univers est 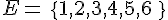$E=\,\{1,2,3,4,5,6\,\}$ , il possède 6 issues.

2.Modélisation d’un expérience aléatoire

Définition :

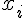
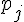
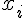
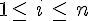
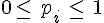
Modéliser une expérience aléatoire, c’est associer à chaque issue x_i , un nombre p_j appelé probabilité de x_i , tel que :Pour tout nombre entier i avec $1\leq\,\,i\,\leq\,\,n$ , $0\leq\,\,p_i\,\leq\,\,1$ et .

3.Modèle d’équiprobabilité

Définition et probabilité :

Lorsque, dans une expérience aléatoire, toutes les issues ont la même probabilité p de se réaliser, on dit qu’il y a équiprobabilité.Si cette expérience aléatoire possède n issues alors 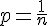$p=\frac{1}{n}$ .

II. Probabilité d’un événement

1.Notion d’événement

Définition :

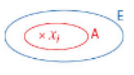
Un événement A est un sous ensemble ( ou une partie) de l’univers E d’une expérience aléatoire.On note 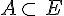$A\subset\,E$ .

Vocabulaire :

Dire qu’une issue de E réalise l’événement A signifie que est un élément de A.
On note $x_i\in\,A$ et on lit x appartient à A.
Une partie $\{\,x_i\,\}$ qui ne contient qu’une issue est appelée événement élémentaire.
L’ensemble vide $\O$ est appelé événement impossible : aucune issue n’appartient à cet ensemble.
L’ensemble E de toutes les issues est appelé événement certain.

2.Probabilité d’un événement

Définition :

La probabilité d’un événement A est la somme des probabilités des issues qui réalisent A.On la note P(A).

Exemple :

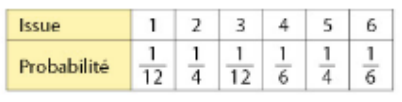
Un dé cubique est truqué de façon que chaque issue ait la probabilité indiquée ci-dessous.

L’événement A : « obtenir un numéro pair » est réalisé par les issues 2,4 et 6.

Donc $P(A),=\frac{1}{4}+\frac{1}{6}+\frac{1}{6}=\frac{7}{12}$ .

Propriété :

Dans une situation d’équiprobabilité, la probabilité d’un événement A est donné par la formule suivante ; $P(A)=\frac{nombre\,issues\,A}{nombre\,issues\,E}$ .

III. Calculs de probabilités

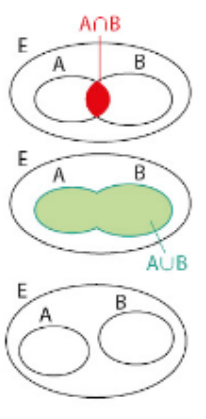
1.Intersection et réunion d’événements

A et B sont deux événements d’un univers E.

Définitions :

L’intersection de A et B est l’événement formé des issues qui réalisent à la fois l’événement A et l’événement B.
On le note $A\cap\,B$ et on lit « A inter B ».
La réunion de A et B est l’événement formé des issues qui réalisent l’événement A ou l’événement B.
On le note $A\,\cup\,B$ et on lit « A union B ».

2.Une formule sur les probabilités.

Propriété :

Pour tout événement A et B. $P(A\,\cap\,B)+P(A\,\cup\,B)=p(A)+P(B)$ .

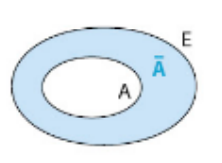
3.Les événements contraires.

Définition :

L’événement contraire à A, noté $\overline{A}$ , est formé des issues qui n’appartiennent pas à A.

Propriété :

Pour tout événement A, $P(A)+P(\overline{A})=1$ .

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «probabilités : cours de maths en 2de à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

D'autres cours et exercices à consulter

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 13 321 027 cours et exercices de maths téléchargés en PDF et 4 250 exercices.