Proportionnalité : corrigé des exercices de maths en 4ème en PDF
Mis à jour le 23 novembre 2025
La proportionnalité est un concept fondamental en mathématiques, essentiel pour les élèves de quatrième. Maîtriser ce sujet permet de développer des compétences cruciales telles que le raisonnement logique et l’analyse de données. Dans cet article, nous vous proposons des corrections d’exercices de mathématiques qui aideront les élèves à renforcer leur compréhension de la proportionnalité et à exceller dans leur apprentissage. Ne manquez pas cette opportunité d’améliorer vos compétences mathématiques !
Exercice 1 – tube d’acier-problème de proportionnalité
Solution 1 :
La masse est proportionnelle à la longueur. On calcule donc la masse d’un tube de 5 m :
Masse de 1 m de tube : 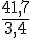
Masse de 1 m de tube : 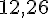
Masse de 5 m de tube : 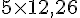
Masse de 5 m de tube : 
Solution 2 :

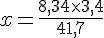

La longueur du tube est donc d’environ 0,68 m.
Exercice 2 – problème du panda-proportionnalité.
1. Masse de bambous mangée en 13 jours :
Un panda mange 
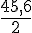
En 13 jours, il mange : 
Calcul :
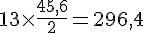
2. Nombre de jours pour manger 1 tonne de bambous :
1 tonne de bambou est 1 000 kg.
Nombre de jours : 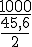
Calcul :
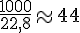
Exercice 3 – calcul de la quatrième proportionnelle
Premier tableau :
On utilise le produit en croix :
Donc, 
En simplifiant, on trouve :
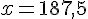
Deuxième tableau :
On utilise le produit en croix :
Donc, 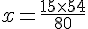
En simplifiant, on trouve :
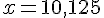
Troisième tableau :
On utilise le produit en croix :
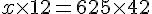
Donc, 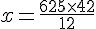
En simplifiant, on trouve :
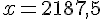
Exercice 4 – mathématiques et environnement
1. Combien de temps faudra-t-il à Marion pour remplir son arrosoir de 10 L ?
Débit de la pompe :
Temps =
Temps =
Temps =
En minutes, Temps =
Donc, cela prendra environ 0,2 minute.
2. Combien de temps faudra-t-il à Marion pour remplir sa citerne de 1 440 L ?
Temps =
Temps =
En minutes, Temps =
Donc, cela prendra environ 29 minutes.
3. Marion a fait fonctionner sa pompe pendant 12 min. Quelle quantité d’eau a-t-elle utilisée ?
Débit :
En heures, Temps =
Quantité d’eau =
4. Si Marion oublie de fermer sa pompe pendant 2 jours, quelle quantité d’eau aura-t-elle utilisée ?
2 jours =
Quantité d’eau =
Exercice 5 – vitesse moyenne et proportionnalité
Convertissons la vitesse de l’objet de m/s en km/h.
1 m/s équivaut à 3,6 km/h, donc pour convertir 100 m/s en km/h, nous faisons :

Ainsi, l’objet se déplace à 360 km/h.
Exercice 6 – vitesse moyenne d’un véhicule.
Pour comparer les deux vitesses, nous devons convertir les vitesses dans la même unité.
La vitesse de Noah est de 2 m/s.
Pour convertir la vitesse de Noah de mètres par seconde en kilomètres par heure, nous utilisons la formule suivante :
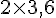
La vitesse d’Emma est de 90 km/h.
En comparant les deux vitesses :
Noah : 7,2 km/h
Emma : 90 km/h
Donc, Emma est plus rapide que Noah.
Exercice 7 – vitesse moyenne d’une girafe
1. a. Convertir 250 m en km.
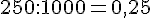
b. Combien de temps met-elle pour parcourir 250 m à cette vitesse ?
Temps = 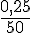
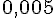
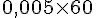
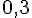
2. Quelle distance parcourt-elle en 3 min à cette vitesse ?
Distance = 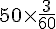
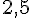
Exercice 8 – eclair et vitesse moyenne, proportionnalité
Pour connaître la distance à laquelle vous vous trouvez de l’éclair, il suffit de multiplier le temps entre l’éclair et le tonnerre par la vitesse du son.
Temps écoulé : 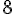
Vitesse du son : 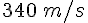
Distance : 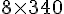
Calcul : 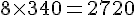
Vous êtes donc à une distance de 2 720 mètres de l’éclair.
Exercice 9 – aire de la portion d’un disque.
Pour calculer l’aire de la zone grisée, nous devons d’abord trouver l’aire du secteur circulaire, puis soustraire l’aire du triangle ABC.
1. Aire du secteur circulaire :
La formule pour l’aire d’un secteur circulaire est :
Où :
En substituant les valeurs :
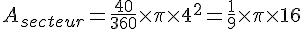
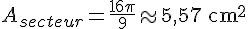
2. Aire du triangle ABC :
Pour trouver l’aire du triangle ABC, nous utilisons :
Avec :
- Ailes (a = b = 4 cm )
- C = 40 °
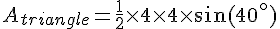
En utilisant 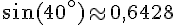
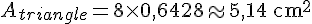
3. Calcul de l’aire de la zone grisée :
L’aire de la zone grisée est la différence entre l’aire du secteur et l’aire du triangle :
Donc, l’aire de la zone grisée est environ (arrondie au dm² près) : 0,43 cm².
Exercice 10 – volume d’eau et proportionnalité.
1. Quel est le volume de glace obtenu à partir de 6 litres de liquide ?
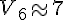
2. Quel volume d’eau liquide faut-il mettre à geler pour obtenir 10 litres de glace ?
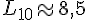
3. Le volume de glace est-il proportionnel au volume d’eau liquide ?
Oui, le volume de glace est proportionnel au volume d’eau liquide car cela forme une droite passant par l’origine.
Coefficient de proportionnalité : 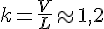
Télécharger ou imprimer cette fiche «proportionnalité : corrigé des exercices de maths en 4ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.


























