Trigonométrie : corrigé des exercices de maths en 3ème en PDF

Mis à jour le 23 novembre 2025

La trigonométrie est un domaine essentiel des mathématiques, particulièrement pour les élèves de troisième, car elle développe des compétences clés comme la résolution de problèmes et l’analyse des formes géométriques. Maîtriser les notions de sine, cosine et tangente permet aux élèves d’appréhender des concepts mathématiques plus avancés. Dans cet article, nous vous proposons des corrections d’exercices de trigonométrie qui aideront les collégiens à renforcer leurs connaissances et à exceller dans cette matière fondamentale.

Exercice 1 – calculs de la mesure d’un angle et trigonométrie.

Figure 1 :

Dans le triangle, nous utilisons la tangente de l’angle en B :

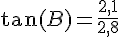
$\tan(B)=\frac{2,1}{2,8}$

Angle B : 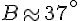$B\approx37^\circ$

Figure 2 :

Dans le triangle, nous utilisons le cosinus de l’angle en L :

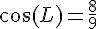
$\cos(L)=\frac{8}{9}$

Angle L : 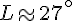$L\approx27^\circ$

Figure 3 :

Dans le triangle, nous utilisons la tangente de l’angle en E :

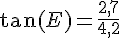
$\tan(E)=\frac{2,7}{4,2}$

Angle E : 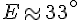$E\approx33^\circ$

Figure 4 :

Dans le triangle, nous utilisons le sinus de l’angle en K :

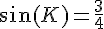
$\sin(K)=\frac{3}{4}$

Angle K : 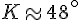$K\approx48^\circ$

Exercice 2 – hauteur d’une tour.

Tour de gauche :

On utilise le triangle rectangle ABC pour calculer la hauteur de la tour h .

La tangente de l’angle $\widehat{BAC}$ est donnée par :

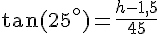
$\tan(25^\circ)=\frac{h-1,5}{45}$

En résolvant pour $ h $ :

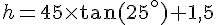
$h=45\times \tan(25^\circ)+1,5$

Calculons :

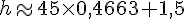
$h\approx45\times 0,4663+1,5$

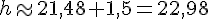
$h\approx21,48+1,5=22,98$

La hauteur de la première tour est donc approximativement 22,98 mètres.

Tour de droite :

On utilise le triangle rectangle ABC. La tangente de l’angle $\widehat{BAC}$ est utilisée pour la hauteur totale, puis on soustrait la hauteur du point A :

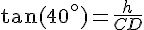
$\tan(40^\circ)=\frac{h}{CD}$

On sait aussi :

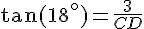
$\tan(18^\circ)=\frac{3}{CD}$

En résolvant pour $ CD $ :

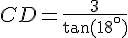
$CD=\frac{3}{\tan(18^\circ)}$

Calculons CD :

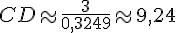
$CD\approx\frac{3}{0,3249}\approx9,24$

En utilisant CD trouvé :

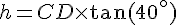
$h=CD\times \tan(40^\circ)$

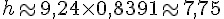
$h\approx9,24\times 0,8391\approx7,75$

La hauteur de la deuxième tour est donc approximativement 7,75 mètres.

Exercice 3 – distance entre deux bateaux.

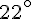
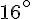
Commençons par identifier les angles dans la configuration triangulaire : d’un côté, nous avons un angle de $22^\circ$ , et de l’autre $16^\circ$ .

La somme des angles d’un triangle étant 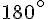$180^\circ$ , nous pouvons déterminer le troisième angle :

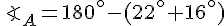
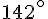
$\angle_A=180^\circ-(22^\circ+16^\circ)$ , soit $142^\circ$ .

Nous utilisons ensuite le théorème des sinus pour trouver la distance entre les deux bateaux :

$\frac{AB}{\sin 142^\circ}=\frac{40}{\sin 22^\circ}$

En résolvant pour 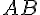, nous trouvons :

$AB=\frac{40\times \sin 142^\circ}{\sin 22^\circ}$

En calculant, nous obtenons :

$AB\approx88,07\ \text{m}$

Donc, la distance séparant les deux bateaux est d’environ 88,07 mètres.

Exercice 4 – bateau et île.

Pour calculer la distance CV, nous devons utiliser le théorème des cosinus dans le triangle CVP.

Considérons le triangle CVP où l’angle 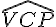$\widehat{VCP}$ est de 70°, CP = 150 m, et CH = 100 m.

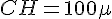
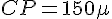
Nous avons : $CH=100\m$ et $CP=150\m$ .

Puisque H est sur la côte, CH est perpendiculaire à la côte, donc CPH est rectangle en H. Cela signifie que HP = 150 m.

En utilisant la trigonométrie : 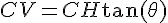$CV=CH\tan(\theta)$ avec $\theta = 70^\circ$ .

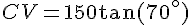
$CV=150\tan(70^\circ)$

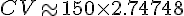
$CV\approx150\times 2.74748$

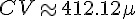
$CV\approx412.12\m$

Ainsi, la distance CV est d’environ 412,12 mètres.

Exercice 5 – problème du géomètre.

Pour calculer la distance GH, on applique le théorème de l’angle externe dans le triangle HAG.

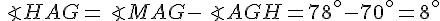
$\angle{HAG}=\angle{MAG}-\angle{AGH}=78^\circ-70^\circ=8^\circ$

Dans le triangle AHG, la somme des angles vaut 180° :

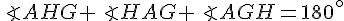
$\angle{AHG}+\angle{HAG}+\angle{AGH}=180^\circ$

Ainsi :

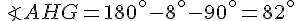
$\angle{AHG}=180^\circ-8^\circ-90^\circ=82^\circ$

Ensuite, on utilise le rapport trigonométrique dans le triangle rectangle AHG :

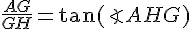
$\frac{AG}{GH}=\tan(\angle{AHG})$

On remplace :

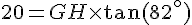
$20=GH\times \tan(82^\circ)$

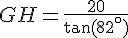
$GH=\frac{20}{\tan(82^\circ)}$

Distance GH : En utilisant une calculatrice, on trouve :

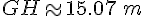
$GH\approx15.07\,m$

Pour calculer la distance GM, on utilise la loi des sinus dans le triangle AGM :

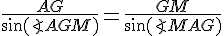
$\frac{AG}{\sin(\angle{AGM})}=\frac{GM}{\sin(\angle{MAG})}$

En remplaçant :

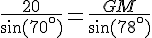
$\frac{20}{\sin(70^\circ)}=\frac{GM}{\sin(78^\circ)}$

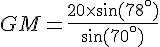
$GM=\frac{20\times \sin(78^\circ)}{\sin(70^\circ)}$

Distance GM : En utilisant une calculatrice, on trouve :

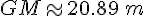
$GM\approx20.89\,m$

Exercice 6 – compléter les pointillés.

a. Dans le triangle ABC rectangle en C, on a :

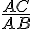
cos $\widehat{BAC}$ = $\frac{AC}{AB}$

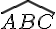
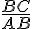
cos $\widehat{ABC}$ = $\frac{BC}{AB}$

b. Dans le triangle BCD, on a :

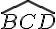
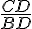
sin $\widehat{BCD}$ = $\frac{CD}{BD}$

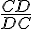
tan $\widehat{DBC}$ = $\frac{CD}{DC}$

c. Dans le triangle ADC, on a :

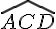
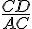
sin $\widehat{ACD}$ = $\frac{CD}{AC}$

Exercice 7 – associer les bonnes formules.

a. Triangle n° 3 : 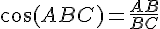$\cos(ABC)=\frac{AB}{BC}$

b. Triangle n° 2 : 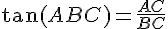$\tan(ABC)=\frac{AC}{BC}$

c. Triangle n° 1 : 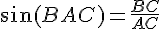$\sin(BAC)=\frac{BC}{AC}$

d. Triangle n° 2 : 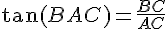$\tan(BAC)=\frac{BC}{AC}$

Exercice 8 – utilisation de la calculatrice.

Pour chaque angle, calculons le sinus et la tangente, arrondis au centième :

Angle	30°	45°	20°	83°	60°
Sinus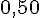
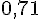
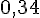
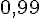
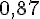
Tangente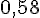

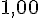
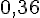
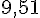
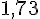
Exercice 9 – produit en croix.

a. Pour résoudre l’équation 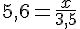$5,6=\frac{x}{3,5}$ , on utilise le produit en croix :

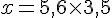
$x=5,6\times 3,5$

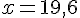
b. Pour résoudre l’équation 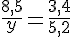$\frac{8,5}{y}=\frac{3,4}{5,2}$ , on utilise le produit en croix :

$8,5\times 5,2=3,4\times y$

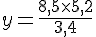
$y=\frac{8,5\times 5,2}{3,4}$

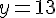
Exercice 10 – calcul de longueurs.

a. Exprime les cosinus, sinus, tangente de l’angle $\widehat{IJK}$ en fonction des longueurs des côtés :

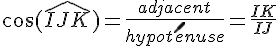
$\cos(\widehat{IJK})=\frac{adjacent}{hypot\acute{e}nuse}=\frac{IK}{IJ}$

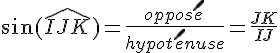
$\sin(\widehat{IJK})=\frac{oppos\acute{e}}{hypot\acute{e}nuse}=\frac{JK}{IJ}$

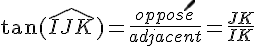
$\tan(\widehat{IJK})=\frac{oppos\acute{e}}{adjacent}=\frac{JK}{IK}$

b. Calcule les longueurs JK et IK en utilisant à chaque fois la formule adéquate :

Pour calculer JK :

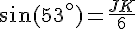
$\sin(53^\circ)=\frac{JK}{6}$

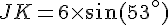
$JK=6\times \sin(53^\circ)$

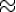
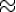
Calcule numérique : JK $\approx$ 6 x 0,7986 $\approx$ 4,79 cm.

Pour calculer IK :

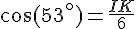
$\cos(53^\circ)=\frac{IK}{6}$

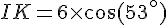
$IK=6\times \cos(53^\circ)$

Calcule numérique :

IK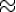 $\approx$ 6 x0,6018 $\approx$ 3,61 cm.

4.9/5 - (37104 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «trigonométrie : corrigé des exercices de maths en 3ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Probabilités

Généralités sur les fonctions

Arithmétique et décomposition en facteurs premiers

Coordonnées géographiques

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 450 971 cours et exercices de maths téléchargés en PDF et 4 250 exercices.