Angles : corrigé des exercices de maths en 5ème en PDF

Mis à jour le 23 novembre 2025

Dans le cadre de leur parcours scolaire, les élèves de cinquième doivent maîtriser les angles, un concept fondamental en géométrie. Comprendre les différents types d’angles, tels que les angles aigus et obtus, est essentiel pour développer des compétences mathématiques clés, notamment la mesure et la construction d’angles. Cet article de corrections d’exercices de mathématiques vous aidera à renforcer vos connaissances et à améliorer votre confiance en la matière.

Exercice 1 – angles complémentaires et supplémentaires.

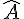
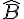
1. Les angles $\widehat{A}$ et $\widehat{B}$ sont complémentaires, donc leur somme est de 90°. Ainsi :

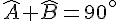
$\widehat{A}+\widehat{B}=90^\circ$

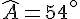
$\widehat{A}=54^\circ$ , donc :

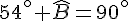
$54^\circ+\widehat{B}=90^\circ$

En soustrayant 54° des deux côtés, on obtient :

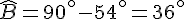
$\widehat{B}=90^\circ-54^\circ=36^\circ$

2. Les angles $\widehat{C}$ et $\widehat{D}$ sont supplémentaires, donc leur somme est de 180°. Ainsi :

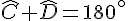
$\widehat{C}+\widehat{D}=180^\circ$

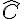
$\widehat{C}$ =84 °, donc :

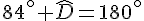
$84^\circ+\widehat{D}=180^\circ$

En soustrayant 84° des deux côtés, on obtient :

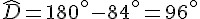
$\widehat{D}=180^\circ-84^\circ=96^\circ$

Exercice 2 – les angles adjacents.

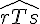
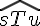
a. $\widehat{rTs}$ et $\widehat{sTu}$

Réponse : oui. Les angles sont adjacents car ils ont un côté commun et partagent le même sommet.

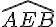
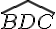
b. $\widehat{AEB}$ et $\widehat{BDC}$

Réponse : non. Les angles ne sont pas adjacents car ils ne partagent ni côté commun ni sommet.

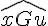
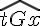
c. $\widehat{xGu}$  et $\widehat{tGx}$

Réponse : non. Les angles ne sont pas adjacents car ils ne partagent pas un côté commun, même s’ils ont le même sommet.

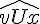
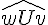
d. $\widehat{vUx}$ et $\widehat{wUv}$

Réponse : oui. Les angles sont adjacents car ils partagent le côté [Uv) et ont le même sommet.

Exercice 3 – les angles opposés par le sommet.

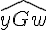
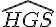
a. Les angles $\widehat{yGw}$ et $\widehat{HGS}$ ne sont pas opposés par le sommet. non.

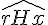
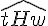
b. Les angles $\widehat{rHx}$ et $\widehat{tHw}$ sont opposés par le sommet. oui.

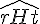
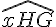
c. Les angles $\widehat{rHt}$ et $\widehat{xHG}$ ne sont pas opposés par le sommet. non.

Exercice 4 – préciser la nature d’un angle.

a. Angles adjacents, angles complémentaires

b. Angles adjacents

c. Angles adjacents, angles supplémentaires

d. Angles adjacents, angles complémentaires

e. Angles adjacents

f. Angles adjacents

Exercice 5 – angles complémentaires ou supplémentaires.

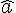
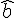
a. Les angles $\widehat{a}$ et $\widehat{b}$ sont complémentaires.

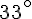
$\widehat{a} = 57^\circ donc \widehat{b} = 90^\circ - 57^\circ =$ $33^\circ$

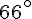
$\widehat{a} = 24^\circ donc \widehat{b} = 90^\circ - 24^\circ =$ $66^\circ$

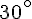
$\widehat{a} = 2 \widehat{b}$ donc $2 \widehat{b} + \widehat{b} = 90^\circ$ , soit $3\widehat{b} = 90^\circ donc \widehat{b} = \frac{90^\circ}{3} =$ $30^\circ$

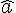
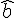
b. Les angles $\widehat{a}$ et $\widehat{b}$ } sont supplémentaires.

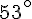
$\widehat{a} = 127^\circ$ donc $\widehat{b} = 180^\circ - 127^\circ$ = $53^\circ$

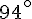
$\widehat{a} = 86^\circ$ donc $\widehat{b} = 180^\circ - 86^\circ =$ $94^\circ$

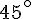
$\widehat{a} = 3 \widehat{b}$ donc $3 \widehat{b} + \widehat{b} = 180^\circ$ , soit $4\widehat{b} = 180^\circ donc \widehat{b} = \frac{180^\circ}{4} =$ $45^\circ$

Exercice 6 – retrouver la position des points.

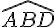
Les angles $\widehat{BAC}$ et $\widehat{ABD}$ sont alternes-internes, donc les points D et C sont à l’opposé des angles autour de la ligne.

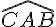
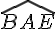
Les angles $\widehat{CAB}$ et $\widehat{BAE}$ sont supplémentaires. Donc, le point E est sur la prolongation de la ligne passant par B.

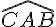
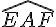
Les angles $\widehat{CAB}$ et $\widehat{EAF}$ sont des angles opposés par le sommet. Ceci indique que le point F est l’opposé du point A.

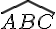
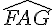
Les angles $\widehat{ABC}$ et $\widehat{FAG}$ sont correspondants, donc le point G se trouve sur la même ligne que A dans le prolongement vers F.

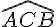
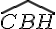
Les angles $\widehat{ACB}$ et $\widehat{CBH}$ sont alternes-internes. Le point H est donc lié au point C.

Exercice 7 – angles correspondants et angles alternes-internes.

a. Deux paires d’angles correspondants, déterminés par la sécante (KC) :

Les angles correspondants sont situés de part et d’autre de la sécante, formant un même angle avec les droites.

Les paires d’angles correspondants par la sécante (KC) sont :

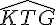
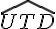
– $\widehat{KTG}$ et $\widehat{UTD}$

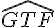
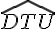
– $\widehat{GTF}$ et $\widehat{DTU}$

b. Deux paires d’angles alternes-internes, déterminés par la sécante (BR) :

Les angles alternes-internes sont situés de part et d’autre de la sécante, entre les deux droites.

Les paires d’angles alternes-internes par la sécante (BR) sont :

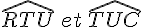
– $\widehat{RTU}\,et\,\widehat{TUC}$

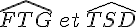
– $\widehat{FTG}\,et\,\widehat{TSD}$

Exercice 8 – calculer mentalement la mesure d’un angle.

Réponse a :

Angle rose : 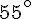$55^\circ$

Angle bleu : 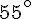$55^\circ$

Angle jaune : 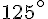$125^\circ$

Réponse b :

Angle rose : 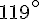$119^\circ$

Angle bleu : 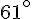$61^\circ$

Angle jaune : 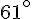$61^\circ$

Exercice 9 – donner la mesure d’un angle.

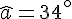
$\widehat{a}=34^\circ$

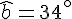
$\widehat{b}=34^\circ$

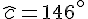
$\widehat{c}=146^\circ$

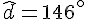
$\widehat{d}=146^\circ$

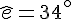
$\widehat{e}=34^\circ$

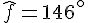
$\widehat{f}=146^\circ$

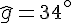
$\widehat{g}=34^\circ$

Exercice 10 – démontrer que les angles ont la même mesure.

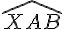
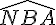
Dans cet exercice, nous devons montrer que les angles $\widehat{XAB}$ et $\widehat{NBA}$ ont la même mesure.

Étant donné que les droites 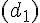et sont parallèles, nous pouvons utiliser la propriété des angles alternes-internes.

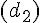
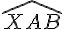
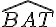
Les angles $\widehat{XAB}$ et $\widehat{BAT}$ sont alternes-internes, donc ils sont égaux :

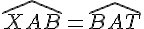
$\widehat{XAB}=\widehat{BAT}$

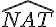
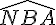
De même, les angles $\widehat{NAT}$ et $\widehat{NBA}$ sont alternes-internes, donc :

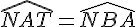
$\widehat{NAT}=\widehat{NBA}$

Comme 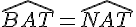$\widehat{BAT}=\widehat{NAT}$ (angle opposé par le sommet), nous pouvons conclure que :

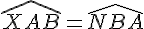
$\widehat{XAB}=\widehat{NBA}$

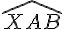
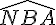
Les angles $\widehat{XAB}$ et $\widehat{NBA}$ ont donc la même mesure.

4.7/5 - (32995 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «angles : corrigé des exercices de maths en 5ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Aires et périmètres de figures

Nombres relatifs

Fractions

Volumes

Priorités opératoires

Triangle

Proportionnalité

Calcul littéral

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 363 559 cours et exercices de maths téléchargés en PDF et 4 250 exercices.