Aires et périmètres de figures : corrigé des exercices de maths en 5ème en PDF

Mis à jour le 23 novembre 2025

Dans cet article, nous allons explorer les aires et les périmètres de figures géométriques, un thème essentiel pour les élèves de cinquième. Comprendre ces concepts mathématiques permet non seulement de renforcer les compétences en géométrie, mais également de développer la logique et la pensée critique des élèves. Grâce à des corrections d’exercices pratiques, les élèves pourront maîtriser ces notions fondamentales et les appliquer dans divers contextes.

Exercice 1 – conversion de surfaces et tableau de conversion

a) 2,6 m² = 260 dm² = 26 000 cm²

$2,6\ \mathrm{m^2} = 260\ \mathrm{dm^2} = 26000\ \mathrm{cm^2}$

b) 3 cm² = 0,3 dm² = 0,0003 m²

$3\ \mathrm{cm^2} = 0,3\ \mathrm{dm^2} = 0,0003\ \mathrm{m^2}$

c) 5,74 km² = 57,4 hm² = 574000 m²

$5,74\ \mathrm{km^2} = 57,4\ \mathrm{hm^2} = 574000\ \mathrm{m^2}$

Exercice 2 – aire de triangle et calcul d’hauteur.

Énoncé : Un triangle d’aire 0,1 dam² a un côté de longueur 800 cm. Calculer la hauteur relative à ce côté.

Conversion des unités : 0,1 dam² = 1000 cm² (car 1 dam = 10 m = 1000 cm, donc 1 dam² = 10000 cm²).

Formule de l’aire du triangle : $A=\frac{1}{2}\times base\times hauteur$

Calcul de la hauteur : Soit A = aire et b = base, ici A = 1000 cm² et b = 800 cm.

On a : $1000=\frac{1}{2}\times 800\times h$

$1000=400\times h$

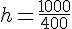
$h=\frac{1000}{400}$

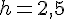
La hauteur relative à ce côté est 2,5 cm.

Exercice 3 – problème de surfaces et conversion d’aires

Étape 1 : Calculer l’aire d’une feuille A4.

Les dimensions d’une feuille A4 sont 21 cm x 29,7 cm. Convertissons ces dimensions en mètres :

$0,21\text{ m} \times 0,297\text{ m}$

Donc, l’aire d’une feuille A4 est :

$0,21\times 0,297=0,06237\text{ m}^2$

Étape 2 : Calculer le poids d’une feuille A4.

1 m² de ce papier pèse 90 g. Donc, une feuille de 0,06237 m² pèse :

$0,06237\times 90=5,6133\text{ g}$

Étape 3 : Calculer le poids de 500 feuilles.

Le poids de 500 feuilles est :

$500\times 5,6133=2806,65\text{ g}$

Étape 4 : Convertir en kilogrammes.

2806,65 g en kilogrammes est :

$2806,65:1000=2,80665\text{ kg}$

Le poids d’une ramette de 500 feuilles de papier A4 est 2,80665 kg.

Exercice 4 – aire d’un trapeze.

Pour calculer l’aire d’un trapèze rectangle, nous utilisons la formule suivante :

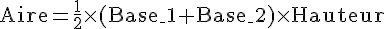
$\text{Aire}=\frac{1}{2}\times (\text{Base\_1}+\text{Base\_2})\times \text{Hauteur}$

Dans notre cas :

Base 1 = 54 m
Base 2 = 35 m
Hauteur = 30 m

En remplaçant ces valeurs dans la formule :

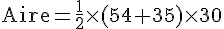
$\text{Aire}=\frac{1}{2}\times (54+35)\times 30$

Calculons :

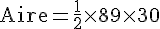
$\text{Aire}=\frac{1}{2}\times 89\times 30$

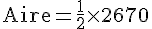
$\text{Aire}=\frac{1}{2}\times 2670$

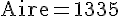
$\text{Aire}=1335$

L’aire du champ est donc 1335 m².

Exercice 5 – calcul de l’aire d’une piece métallique.

Étape 1 : Calculons l’aire du losange.

L’aire du losange est donnée par la formule : $\frac{D\times d}{2}$ , où D et d sont les diagonales.

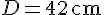
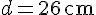
Nous avons : $D=42\,\text{cm}$ et $d=26\,\text{cm}$

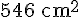
Aire du losange = $\frac{42\times 26}{2}$ = $546\,\text{cm}^2$

Étape 2 : Calculons l’aire du cercle.

L’aire du cercle est donnée par la formule : $\pi r^2$ .

Nous avons : 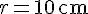$r=10\,\text{cm}$

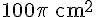
Aire du cercle = $\pi\times 10^2$ = $100\pi\,\text{cm}^2$

Étape 3 : Calculons l’aire hachurée.

Aire hachurée = Aire du losange – Aire du cercle

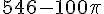
= $546-100\pi$

= (en prenant $\pi \approx 3,1416$ )

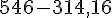
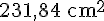
= $231,84\,\text{cm}^2$

L’aire hachurée est 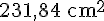$231,84\,\text{cm}^2$

Exercice 6 – calcul de l’aire d’une figure géométrique.

Calcul de l’aire du triangle :

Le triangle ABF est un triangle rectangle. Sa base BF mesure 17 mm et sa hauteur AH mesure 90 mm.

L’aire du triangle est donnée par la formule :

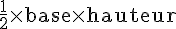
$\frac{1}{2}\times \text{base}\times \text{hauteur}$

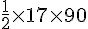
$\frac{1}{2}\times 17\times 90$

mm²

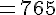
Calcul de l’aire du rectangle :

Le rectangle BFHC a une largeur BF de 17 mm et une longueur de 16 mm.

L’aire du rectangle est donnée par la formule :

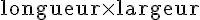
$\text{longueur}\times \text{largeur}$

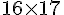
$16\times 17$

mm²

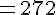
Calcul de l’aire totale de la figure :

L’aire totale est la somme de l’aire du triangle et de l’aire du rectangle :

mm²

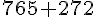
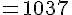
Exercice 7 – calcul de l’aire d’une figure.

1. Calculer le rayon R du cercle :

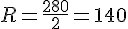
$R=\frac{280}{2}=140$

2. Calculer l’aire du trapèze :

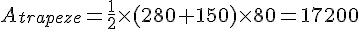
$A_{trapeze}=\frac{1}{2}\times (280+150)\times 80=17200$

3. Calculer l’aire du rectangle :

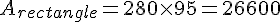
$A_{rectangle}=280\times 95=26600$

4. Calculer l’aire du demi-disque :

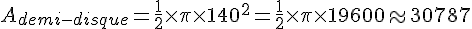
$A_{demi-disque}=\frac{1}{2}\times \pi\times 140^2=\frac{1}{2}\times \pi\times 19600\approx30787$

5. Calculer l’aire totale :

$A_{total}=A_{trapeze}+A_{rectangle}+A_{demi-disque}=17200+26600+30787\approx 74587$

Exercice 8 – périmètre et aire d’une figure

Calcul du périmètre :

Pour calculer le périmètre de la figure, il faut additionner la longueur de tous ses côtés extérieurs.

La figure est constituée de trois rectangles mis ensemble.

Longueur totale :

Horizontalement : 6 cm
Verticalement : 4,5 cm

Les segments horizontaux (de gauche à droite) et verticaux (de bas en haut) sont :

Côté inférieur : 6 cm
Côté droit : 4,5 cm
Côté supérieur :
- – Partie supérieure gauche : 2 cm (3 segments de 2 cm chacun)
- – Partie supérieure droite : non mesurée mais constituée par les restes verts, 2 segments visibles de l’image (4.5/3 = 1,5 chaque segment)
Côté gauche : 4,5 cm

Le périmètre est donc :

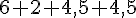
Calcul de l’aire :

L’aire de la figure peut être calculée en décomposant la figure en trois rectangles distincts :

Rectangle 1 : 6 cm × 1,5 cm
Rectangle 2 : 4 cm × 1,5 cm
Rectangle 3 : 2 cm × 1,5 cm

Soit en unités :

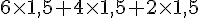
$6\times 1,5+4\times 1,5+2\times 1,5$

Ce qui donne :

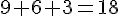
Le périmètre est 19 cm et l’aire est 18 cm².

Exercice 9 – calcul du périmètre d’une figure.

Pour calculer le périmètre de cette figure, nous devons additionner les côtés droits et les courbes semi-circulaires.

Étape 1 : Calculer le périmètre des parties rectangulaires.

Le rectangle a une longueur de 6 cm et une hauteur de 3 cm. Étant donné les deux côtés du rectangle couverts par la figure, il nous reste :

Longueur totale du bas + Longueur totale du haut – 2 x Largeur (car la largeur est interrompue par les demi-cercles).

Étape 2 : Calculer le périmètre des courbes.

Chaque courbe est un demi-cercle. Pour calculer la longueur totale des deux courbes :

Rayon d’un demi-cercle = 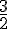$\frac{3}{2}$

Périmètre d’un cercle = 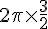$2\pi\times \frac{3}{2}$

Longueur d’un demi-cercle = 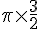$\pi\times \frac{3}{2}$

Étape 3 : Additionner toutes les longueurs pour obtenir le périmètre total.

Périmètre total = 6 + 6 – 3 + \pi \cdot 3 = 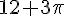$12+3\pi$

Approximativement, cela donne : 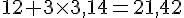$12+3\times 3,14=21,42$

Le périmètre de la figure est d’environ 21,42 cm.

Exercice 10 – calculs d’aires de triangles et conversions d’aires.

a. Conversion de 12 m² en dm² :

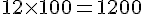
$12\times 100=1200$

b. Conversion de 1,32 dm² en cm² :

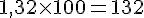
$1,32\times 100=132$

c. Conversion de 4,5 cm² en m² :

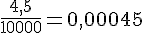
$\frac{4,5}{10000}=0,00045$

d. Conversion de 8 552 m² en km² :

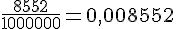
$\frac{8552}{1000000}=0,008552$

4.7/5 - (31121 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «aires et périmètres de figures : corrigé des exercices de maths en 5ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Symétrie centrale

Proportionnalité

Volumes

Priorités opératoires

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 363 691 cours et exercices de maths téléchargés en PDF et 4 250 exercices.