Volumes : corrigé des exercices de maths en 5ème en PDF

Mis à jour le 23 novembre 2025

Les volumes sont une notion clé pour les élèves de cinquième, car ils permettent de comprendre comment mesurer l’espace occupé par des objets en trois dimensions. Maîtriser cette compétence est essentiel pour résoudre des problèmes pratiques et développer des compétences en géométrie et en calcul. Dans cet article, nous allons corriger divers exercices de mathématiques liés aux volumes, afin d’aider les élèves à renforcer leur compréhension et à exceller dans cette matière fondamentale.

Exercice 1 – calculer le volume d’une pièce.

Pour calculer le volume du mur constitué par les cinq pièces, on utilise la formule du volume d’un parallélépipède rectangle :

$V=L\times l\times h$

Où :

L = 9 cm (longueur)
l = 2 cm (largeur ou épaisseur)
h = 4 cm (hauteur)

En substituant les valeurs, on obtient :

$V=9\times 2\times 4$

Calculons le volume :

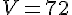
Donc, le volume du mur est de 72 cm³.

Exercice 2 – volume d’un casier à bouteilles.

1. Calculer le volume du pavé droit à partir duquel a été formé le casier.

Le volume du pavé droit est donné par la formule :

$V=L\times l\times h$

Avec L = 42 cm, l = 36 cm, et h = 36 cm}, on obtient :

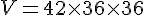
$V=42\times 36\times 36$

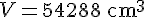
$V=54288\,\text{cm}^3$

2. Calculer le volume intérieur d’un compartiment.

Le volume d’un cylindre est donné par la formule :

$V=\pi \times r^2 \times h$

Le rayon $r = \frac{10}{2} = 5$ cmet la hauteur h = 36 cm.

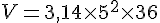
$V=3,14\times 5^2\times 36$

$V=2826\, cm^3$

3. En déduire le volume de plastique.

Le casier contient neuf compartiments, donc le volume total des cylindres est :

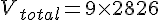
$V_{total}=9\times 2826$

$V_{total}=25434\, cm ^3$

Le volume de plastique est la différence entre le volume du pavé et le volume des cylindres :

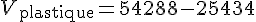
$V_{\text{plastique}}=54288-25434$

$V_{\text{plastique}}=28854\, cm ^3$

Exercice 3 – perspective cavalière d’un prisme droit.

Combien mesure la hauteur de ce prisme droit ? : 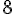cm

Nommer les bases : Les bases sont les triangles ABC et DEF.

Nommer les faces latérales : Les faces latérales sont les rectangles ABED, BCFE, et CAFD.

Combien mesure la longueur DF ? : 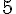cm

Combien mesure la longueur BE ? : 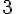cm

Exercice 4 – compléter un parallélépipède rectangle avec des cubes.

Dans la hauteur :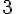

Dans la largeur :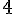

Dans la longueur :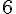

Exercice 5 – convertir des volumes.

1 m³ en dm³ : $1\ m^3=1000\ dm^3$

0,087 m³ en cm³ : $0,087\ m^3=87000\ cm^3$

345 000 mm³ en m³ : $345000\ mm^3=0,000345\ m^3$

0,375 m³ en dm³ : $0,375\ m^3=375\ dm^3$

38 m³ en dm³ : $38\ m^3=38000\ dm^3$

0,00043 m³ en dm³ : $0,00043\ m^3=0,43\ dm^3$

2915 cm³ en dm³ : $2915\ cm^3=2,915\ dm^3$

740 cm³ en dm³ : $740\ cm^3=0,74\ dm^3$

8,5 cm³ en dm³ : $8,5\ cm^3=0,0085\ dm^3$

0,37 dm³ en cm³ : $0,37\ dm^3=370\ cm^3$

0,005 m³ en cm³ : $0,005\ m^3=5000\ cm^3$

47 mm³ en cm³ : $47\ mm^3=0,047\ cm^3$

Exercice 6 – calcul du volume d’une tente.

Pour calculer le volume de la tente, il faut multiplier l’aire de la base par la hauteur du prisme.

Étape 1 : Calcul de l’aire de la base

La base de la tente est un triangle isocèle. L’aire d’un triangle est donnée par la formule :

$Aire=\frac{1}{2}\times base \times hauteur$

La base est BC = 1,5 m. La hauteur (AH) est la ligne perpendiculaire entre A et le segment BC.

Considérons que les côtés AB et AC sont égaux, on peut utiliser le théorème de Pythagore pour trouver AH en supposant que H est le milieu de BC.

Donc HC = 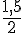$\frac{1,5}{2}$ = 0,75 m.

AB et AC forment les côtés égaux du triangle isocèle :

En utilisant le théorème de Pythagore dans le triangle rectangulaire AHC :

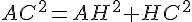
Supposons AC = x :

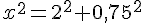
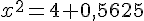
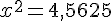
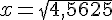
$x=\sqrt{4,5625}$

Calculons la hauteur AH :

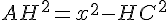
Si AH = 2 m, alors :

On a :

$Aire_\triangle=\frac{1}{2}\times BC \times AH= \frac{1}{2}\times 1,5 \times 2$

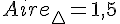
$Aire_\triangle=1,5$

Étape 2 : Calcul du volume du prisme

Le volume du prisme est donné par :

$Volume=Aire\_base \times hauteur$

Avec la longueur CD = 4,5 m :

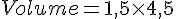
$Volume=1,5\times 4,5$

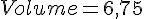
Le volume de la tente est de 6,75 m³.

Exercice 7 – calcul du volume d’un prisme.

Pour calculer le volume d’un prisme droit, on utilise la formule :

$V=Base\times hauteur$

Dans cet exercice, la base est un quadrilatère ABCD d’aire $A=15\ cm^2$ .

La hauteur du prisme est $h=5\ cm$ .

En appliquant la formule, on obtient :

$V=15\ cm^2\times 5\ cm$

$V=75\ cm^3$

Donc, le volume du prisme est 75 cm³.

Exercice 8 – volume d’un hangar.

1. Calculer la hauteur AH’ du triangle isocèle ABE.

Dans le triangle isocèle ABE, la hauteur AH’ coupe la base BE en son milieu. Ainsi, $BH' = EH' = \frac{BE}{2} = \frac{9}{2} = 4,5 \, m$ .

En utilisant le théorème de Pythagore dans le triangle ABH’, on a :

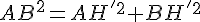
$AB^2=AH^{'2}+BH^{'2}$

Avec AB = AH = 12,5 m :

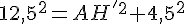
$12,5^2=AH^{'2}+4,5^2$

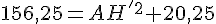
$156,25=AH^{'2}+20,25$

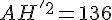
$AH^{'2}=136$

$AH'=\sqrt{136}\approx11,66\, \text{m}$

2. Calculer l’aire du polygone ABCDE.

L’aire du polygone ABCDE est la somme de l’aire du rectangle BCDE et de l’aire du triangle ABE.

Pour le rectangle BCDE :

$\text{Aire}_{BCDE}=CD \times DE = 9 \times 5,2 = 46,8\,\text{m}^2$

Pour le triangle ABE :

$\text{Aire}_{ABE}=\frac{1}{2} \times BE \times AH' = \frac{1}{2} \times 9 \times 11,66 \approx 52,47\,\text{m}^2$

Aire totale :

$\text{Aire}_{ABCDE}=46,8 + 52,47 \approx 99,27\,\text{m}^2$

3. En déduire le volume du hangar.

Le volume du hangar est la somme du volume du pavé droit (parallélépipède rectangle) BCDFGH et du volume du prisme droit ABEFHG.

Volume du pavé BCDFGH :

$V_{BCDFGH}=CD \times DE \times AH = 9 \times 5,2 \times 12,5 = 585\,\text{m}^3$

Volume du prisme ABEFHG :

$V_{ABEFHG}=\text{Aire}_{ABE} \times AH' = 52,47 \times (16-12,5)$

$=52,47 \times 3,5 \approx 183,65\,\text{m}^3$

Volume total du hangar :

$V_{\total}=585 + 183,65 \approx 768,65\,\text{m}^3$

Exercice 9 – etude d’une piscine.

1. Par quelles lettres désigne-t-on les bases de ce prisme ?

Les bases sont désignées par les lettres ABCD et EFGH.

2. Quelle est la nature géométrique des bases de ce prisme ?

Les bases sont des rectangles.

3. Quelles sont les dimensions d’une base ?

Une base mesure 8 m par 2 m.

4. Quelle est l’aire de la base ?

L’aire de la base est : 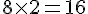$8\times 2=16$ m².

5. Quelle est l’aire de ce prisme ?

L’aire latérale se calcule en considérant le périmètre de la base (8 + 2 + 8 + 2 = 20 m) multiplié par la hauteur (4 m) : 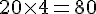$20\times 4=80$ m².

L’aire totale est la somme de l’aire latérale et deux fois l’aire de la base :

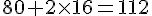
$80+2\times 16=112$ m².

6. Par quelles lettres désigne-t-on les 4 faces latérales de ce prisme ?

Les faces latérales sont désignées par les lettres ABFE, BCGF, CDHG et DAEH.

7. Quelle est la hauteur de ce prisme ?

La hauteur est de 4 m.

8. En déduire le volume de ce prisme ?

Le volume est donné par la formule 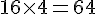$16\times 4=64$ m³.

9. On remplit le volume de ce prisme au quatre cinquième d’eau. Calculer en litres le volume d’eau.

Volume d’eau = 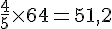$\frac{4}{5}\times 64=51,2$ m³ = 51 200 litres.

Exercice 10 – volume d’un flacon de parfum.

a) Calculer l’aire de la base en blanc sur le dessin de droite, puis calculer le volume intérieur du flacon en cm³.

L’octogone régulier peut être divisé en 8 triangles isocèles. L’aire d’un tel triangle est calculée avec :

$\frac{1}{2} \times \text{base} \times \text{hauteur}$

La base des triangles est 2,3 cm et la hauteur est 2,8 cm :

$\frac{1}{2} \times 2,3 \times 2,8 = 3,22 \, \text{cm}^2$

L’aire de l’octogone est donc :

$8 \times 3,22 = 25,76 \, \text{cm}^2$

Le volume du flacon est le produit de l’aire de la base par la hauteur :

$25,76 \times 12 = 309,12 \, \text{cm}^3$

b) Calculer l’aire de l’étiquette.

L’étiquette est un rectangle autour du flacon, sa hauteur est 3,5 cm et sa longueur est égale au périmètre de l’octogone.

Le périmètre de l’octogone est :

$8 \times 2,5 = 20 \, \text{cm}$

Donc, l’aire de l’étiquette est :

$20 \times 3,5 = 70 \, \text{cm}^2$

4.8/5 - (35005 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «volumes : corrigé des exercices de maths en 5ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Priorités opératoires

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 363 559 cours et exercices de maths téléchargés en PDF et 4 250 exercices.