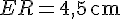Parallélogramme : corrigé des exercices de maths en 5ème en PDF
Mis à jour le 23 novembre 2025
Exercice 1 – construction – parallélogramme
Pour vérifier la construction du parallélogramme ABCD, il faut s’assurer que les côtés opposés sont égaux. Dans ce cas :
On sait que :

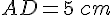
Il est nécessaire de trouver les mesures des côtés [AB] et [BC] grâce à la propriété du parallélogramme.
Ensuite, on utilise les propriétés des angles :
La somme des angles dans un parallélogramme est de 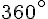
Si l’angle 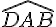
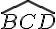
Calculons les angles restants :
En vérifiant ces angles et longueurs, nous confirmons que ABCD est bien un parallélogramme.
Exercice 2 – les parallélogrammes particuliers.
Construction : Tracer le triangle EFG avec EG = 8 cm, 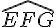
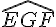
Symétrie : Soit H et I les symétriques respectifs de F et G par rapport à E.
Nature de IFGH :
Dans le quadrilatère IFGH :
- Le segment FG est parallèle et de même longueur que le segment HI (par symétrie),
- Le segment IF est parallèle et de même longueur que le segment HG (par symétrie).
Conclusion : Le quadrilatère IFGH est donc un parallélogramme car il a ses côtés opposés parallèles et de même longueur.
Exercice 3 – construction de parallélogramme
Étape 1 : Tracer le segment OR
1. Tracer un segment OR tel que 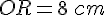
Étape 2 : Tracer l’angle ORU
2. À l’aide du rapporteur, tracer un angle 
Étape 3 : Tracer le segment RU
3. Sur le côté de l’angle de 120 degrés, tracer le segment RU tel que 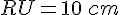
Étape 4 : Compléter le parallélogramme
4. Tracer le segment OS parallèle et égal à RU, et le segment SU parallèle et égal à OR pour compléter le parallélogramme OURS.
Étape 5 : Vérification
5. Vérifier que les côtés opposés sont égaux et parallèles, confirmant ainsi la construction du parallélogramme.
Exercice 4 – construction à la règle et au compas
Construction :
Pour construire le parallélogramme BRUN de centre E, suivez les étapes ci-dessous :
- Placez le point E.
- Tracez un cercle de centre E avec un rayon de 3,5 cm pour trouver le point B.
- Tracez un cercle de centre E avec un rayon de 4,5 cm pour trouver le point R.
- Assurez-vous que le point B est à 5 cm du point R. Ajustez si nécessaire en utilisant la distance BR=5 cm.
- Tracez les segments BR, RU, UN et NB pour compléter le parallélogramme.
Vérification :
- Vérifiez que les diagonales se coupent en leur milieu au point E,
ce qui confirme que E est bien le centre du parallélogramme. - Avec les mesures données :
Calculs :
- Distance BE = 3,5 cm :
- Distance ER = 4,5 cm :
- Distance BR = 5 cm :
Ces vérifications confirment que le parallélogramme est correctement construit.
Exercice 5 – démontrer que la figure est un rectangle.
Construction :
1. Tracez le segment [DM] de 7 cm.
2. À partir du point D, construisez un angle de 32 ° pour déterminer la direction de ( MO ).
3. À partir du point M , construisez un angle de 58 ° pour déterminer la direction de ( DO ).
4. Complétez le parallélogramme en traçant les côtés (DI) et (MI) parallèles respectivement à (MO) et (DO) .
Démonstration que DOMI est un rectangle :
Propriété d’un rectangle : Un rectangle est un parallélogramme avec au moins un angle droit.
Calcul des angles du parallélogramme :
Dans le triangle DMO :
Conclusion : Comme le parallélogramme DOMI a un angle droit 
Exercice 6 – construire un parallélogramme.
Étapes de construction :
1. Tracez le segment ![[AB]](https://maths-pdf.fr/latex-images/5e32d4dbe98ef3af1b5123ccba43cbf7.png)
2. Placez le point C tel que 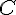
3. Tracez ![[AC]](https://maths-pdf.fr/latex-images/3ec2b68785ef743e4896d19fb83e1e79.png)
![[AB]](https://maths-pdf.fr/latex-images/5e32d4dbe98ef3af1b5123ccba43cbf7.png)
![[AC]](https://maths-pdf.fr/latex-images/3ec2b68785ef743e4896d19fb83e1e79.png)
4. Complétez le parallélogramme en traçant ![[CD]](https://maths-pdf.fr/latex-images/c1b706bf8595d9bc11fdee01201138a8.png)
![[DA]](https://maths-pdf.fr/latex-images/2231ad70391dd609446cf564bb39fc9f.png)
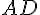
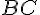
![[BD]](https://maths-pdf.fr/latex-images/e175905feb1843b45058f30c40c99249.png)
![[AC]](https://maths-pdf.fr/latex-images/3ec2b68785ef743e4896d19fb83e1e79.png)
5. Vérifiez que les diagonales se croisent en leur milieu, prouvant qu’il s’agit d’un parallélogramme.
Exercice 7 – construire un parallélogramme.
Étape 1 : Tracer le segment [IJ] de 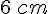
Étape 2 : À partir du point I, tracer un cercle de rayon 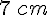
Étape 3 : À partir du point J, tracer un cercle de rayon 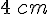
Étape 4 : L’intersection de ces deux cercles donne le point K. Relier les points K et J, puis K et I.
Étape 5 : Tracer le segment [KL] parallèle au segment [IJ] et [IL] parallèle au segment [JK] pour obtenir le point L.
Conclusion : Relier enfin les points L et J pour former le parallélogramme IJKL.
Exercice 8 – construction en vraie grandeur.
Pour construire le parallélogramme FGHI en vraie grandeur, suivez ces étapes :
1. Tracez d’abord le segment FG de 6 cm.
2. À partir du point F, tracez un arc de cercle de 4,3 cm.
3. À partir du point G, tracez un arc de cercle de 3 cm qui croise le précédent arc. Le point d’intersection des deux arcs est le point J.
4. Reliez F à J, J à G, et tracez IJ et JH pour compléter le parallélogramme.
Vérifiez que les côtés opposés sont bien parallèles et de même longueur pour confirmer que c’est un parallélogramme.
Exercice 9 – construire un parallélogramme.
Étape 1 : Dessiner le segment [OI] de 7 cm.
Étape 2 : À partir du point O, tracer un angle de 75° avec le segment [OI].
Étape 3 : À partir du point O, tracer un segment [OL] de 4 cm dans la direction de l’angle de 75°.
Étape 4 : À partir des points I et L, tracer des segments parallèles à [OL] et [OI] respectivement pour former le parallélogramme JOLI.
Conclusion : Le parallélogramme JOLI est maintenant construit, vérifiant les conditions de longueur et d’angle données.
Exercice 10 – construction d’un parallélogramme.
Pour construire le parallélogramme ABCD, suivez les étapes ci-dessous :
- Commencez par tracer le segment DE de 5 cm.
- Puis, à partir du point E, tracez l’angle de 80° avec une règle et un rapporteur.
- Tracez le segment EC d’une longueur de 2,5 cm.
- À partir des points D et C, tracez des lignes parallèles aux segments EC et DE, respectivement.
- Ces lignes se croisent aux points A et B, formant le parallélogramme ABCD.
Les diagonales se coupent perpendiculairement car nous avons créé deux angles de 80° de chaque côté de la ligne DE.
Vérification : Assurez-vous que les côtés opposés du parallélogramme sont égaux et parallèles :
- AB = CD
- BC = DA
Télécharger ou imprimer cette fiche «parallélogramme : corrigé des exercices de maths en 5ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.