Symétrie centrale : corrigé des exercices de maths en 5ème en PDF

Exercice 1 – symétrie centrale – bonhomme de neige

Pour construire la symétrie centrale de la figure par rapport au point I, suivez les étapes suivantes :

1. Identifier les points de la figure : Prenez chaque point de la figure (extrémités des bras, haut du chapeau, etc.) et notez leurs coordonnées par rapport à un repère avec une origine au point I.

2. Appliquer la symétrie centrale : La symétrie centrale par rapport à un point consiste à inverser les coordonnées de chaque point par rapport à ce point de symétrie. Si un point a pour coordonnées (x, y) par rapport au point I considéré comme origine, son image par symétrie aura pour coordonnées (-x, -y).

3. Tracer les nouveaux points : Placez chaque point symétrique à la position souhaitée en appliquant le principe de la symétrie centrale. Par exemple, si un point initial est à droite et vers le haut par rapport à I, son symétrique sera à gauche et vers le bas à la même distance de I.

4. Relier les points : Une fois que tous les points symétriques sont placés, reliez-les de sorte à former la figure symétrique complète, assurant l’exactitude des proportions et angles.

Le bonhomme de neige symétrique devrait apparaître inversé, mais à dimension et proportion égales par rapport à I.

Exercice 2 – symétrie centrale – chaussures

Pour construire l’image de la figure par rapport au centre O, suivez les étapes ci-dessous :

1. Pour chaque point de la figure initiale (A, B, C, D, E, F, G, H, I), tracez une droite passant par ce point et le centre O.

2. Reportez la mesure de la distance de chaque point au centre O de l’autre côté pour obtenir le point symétrique. Utilisez une règle pour mesurer la distance entre le point et O, puis prolongez la droite au-delà du centre O avec la même distance.

3. Les nouveaux points obtenus (appellés A’, B’, C’, D’, E’, F’, G’, H’, I’) représentent l’image de la figure.

4. Reliez les points obtenus dans l’ordre approprié pour reconstituer la figure symétrique.

Assurez-vous que chaque point et son image soient bien alignés par rapport au centre O.

Voici un exemple visuel de ce procédé appliqué à un point de la figure :

Exercice 3 – symétrie centrale et propriétés.

1. Construction des points S et T :

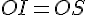
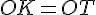
Les points S et T sont les symétriques respectifs des points I et K par rapport au point O, donc et .

2. Parallélisme et égalité de longueurs :

Comme S et T sont les symétriques des points I et K, les droites (TI) et (KS) sont parallèles car elles sont les symétriques l’une de l’autre. De plus, on a car chaque point est à égale distance d’O dans la transformation par symétrie centrale.

3. Égalité des angles :

Les angles et sont égaux car les transformations par réflexion maintiennent les angles.

4. Alignement des points S, J, et T :

Les points S, J, et T sont alignés car la symétrie centrale conserve l’alignement lorsqu’il y a une symétrie centrale avec O comme centre. Ainsi, O étant le milieu de [JR], J est symétrique à lui-même par rapport à O.

Exercice 4 – propriétés de la symétrie centrale – démontrer.

1.a. Placer quatre points A, B, I et J non alignés.

1.b. Construire les points C et D qui sont les symétriques des points A et B par rapport au point I.

1.c. Construire les points F et E qui sont les symétriques des points C et D par rapport au point J.

2. Quelle est la symétrique de la demi-droite [AB] par rapport au point I ?

La symétrique de la demi-droite [AB] par rapport au point I est la demi-droite [CD].

Quelle est la symétrique de la demi-droite [CD] par rapport au point J ?

La symétrique de la demi-droite [CD] par rapport au point J est la demi-droite [EF].

3. Les demi-droites [AB] et [FE] sont-elles parallèles ?

Oui, les demi-droites [AB] et [FE] sont parallèles car les symétries centrales conservent le parallélisme.

Sont-elles de même sens ?

Non, les demi-droites [AB] et [FE] ne sont pas de même sens car les symétries centrales inversent le sens des demi-droites.

Exercice 5 – centre de symétrie d’une figure.

a. Pour que le point O soit le centre de symétrie, il faut compléter la figure en ajoutant une ligne et un cercle à droite du point O, mirroring ce qui est à gauche.

b. Pour que le point O soit le centre de symétrie, il faut prolonger la ligne en zigzag à partir de O de manière symétrique à gauche et ajouter une ligne horizontale qui complète la symétrie par rapport au centre O.

Exercice 6 – symétrie centrale d’une figure.

1. Identifiez le centre de symétrie S .

2. Prenez chaque point de la figure et tracez un segment de droite entre ce point et S.

3. Prolongez ce segment de manière à ce que S soit le milieu du segment. Ainsi, vous obtenez le symétrique de chaque point de la figure par rapport à S.

4. Répétez l’opération pour tous les points de la figure (y compris les intersections importantes comme le centre du cercle ( X ) pour obtenir le nouveau triangle et le cercle.

5. Dessinez le symétrique du cercle en plaçant son centre symétrique et en traçant un cercle de même rayon.

6. Pour les lignes droites, tracez leur symétrique en obtenant deux points symétriques sur la ligne, puis prolongez la ligne entre ces deux nouveaux points.

Les traits de construction doivent être laissés apparents pour montrer le procédé de symétrie.

Exercice 7 – symétrie centrale d’une figure.

1. Construction de la figure :

Étapes à suivre :

1. Tracez un segment [AB] de longueur 5 cm.

2. Positionnez le point C tel que = 30 ° et = 45 °.

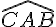
2. Symétrie centrale par rapport à O :

Pour construire la symétrie de chaque point de la figure par rapport au point O :

– Trouvez le point C’ tel que O soit le milieu du segment [CC’].

– Répétez pour les points A et B pour obtenir A’ et B’.

La figure symétrique de la figure initiale par rapport à O est le triangle A’B’C’ avec le même cercle passant par A’ et B’.

Exercice 8 – symétrie centrale d’un chat.

Pour construire la figure symétrique du chat par rapport au point Q, suivez les étapes suivantes :

1. Pour chaque point de la figure (A, B, C, …, P), tracez son symétrique par rapport à Q. Par exemple, pour le point A, trouvez un point A’ tel que Q soit le milieu du segment [AA’].
2. Pour cela, utilisez la propriété de la symétrie centrale : si un point M a pour symétrique M’ par rapport à Q, alors et les segments [MQ] et [QM’] sont sur le même axe.
3. Répétez le procédé pour chaque point de la figure originale.
4. Une fois tous les points symétriques trouvés, reliez-les dans le même ordre que les points d’origine pour obtenir la figure symétrique complète.

Exercice 9 – symétrie centrale de cercles.

Étape 1 : Construire la figure donnée.

Définition du triangle :

Le triangle ACD est isocèle et rectangle en C, donc AC = CDet les angles 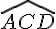et mesurent chacun 45 °.

Longueur des côtés :

cm

Pour le segment [AB], C est le milieu, donc AC = CB = 3 cm.

Vérifiez les mesures avec le théorème de Pythagore:

cm, donc il est correct.

Demi-cercles :

Les demi-cercles ont pour diamètres respectifs [AC] et [CB] et leur rayon est alors 3 cm.

Étape 2 : Construire le symétrique de cette figure par rapport au point O (milieu du segment [AB]).

Symétrie centrale :

Chaque point de la figure initiale a un symétrique de l’autre côté de O à la même distance :

• A devient B’ tel que O est le milieu de [BB’].
• B devient A’ tel que O est le milieu de [AA’].
• Les demi-cercles deviennent symétriques à l’opposé de O.

Vérifiez en traçant ces points et les arcs avec les outils géométriques pour obtenir une construction précise.

Exercice 10 – construction de symétries centrales.

1. Construire le symétrique de chaque figure par rapport à O.

– Pour la première figure, placez chaque point à une distance égale de O mais de l’autre côté de O.

Reproduisez la figure en respectant les formes et dimensions.

– Pour la deuxième figure, procédez de la même façon en vous assurant que chaque point est à une distance identique et opposée par rapport à O.

– Répétez ces étapes pour la troisième figure dans la série.

2. Construire le symétrique de chaque figure par rapport à O (grille triangulaire).

– Identifiez les coordonnées des sommets par rapport à O.

Reflétez chaque point à travers O et connectez-les dans l’ordre initial pour obtenir le symétrique.

3. Construire le symétrique de chaque figure par rapport à O puis par rapport à (d).

– D’abord, effectuez la symétrie centrale par rapport à O comme dans les étapes précédentes.

– Ensuite, utilisez la ldroite (d) pour effectuer une symétrie axiale du résultat.

Chaque point de la figure doit être réfléchi équidistantement de la ligne (d).

Remarque : Utilisez deux couleurs différentes pour différencier la symétrie centrale de la symétrie axiale.