Triangle : corrigé des exercices de maths en 5ème en PDF

Exercice 1 – médiane, médiatrice et hauteur

Médiane : Une médiane d’un triangle est un segment qui relie un sommet du triangle au milieu du côté opposé. Par exemple, dans le triangle ABC, la médiane issue de A serait le segment [AM] où M est le milieu de [BC].

Médiatrice : La médiatrice d’un côté d’un triangle est la droite qui est perpendiculaire à ce côté et qui le coupe en son milieu. Par exemple, pour le côté [EF] du triangle DEF, la médiatrice serait perpendiculaire à [EF] et passerait par son milieu.

Hauteur : Une hauteur d’un triangle est un segment de droite perpendiculaire à un côté (ou à son prolongement) et passant par le sommet opposé. Par exemple, dans le triangle GHI, la hauteur issue de H serait le segment perpendiculaire à [GI] passant par H.

Exercice 2 – cercle circonscrit à un triangle

Construction du triangle :

1. Trace le segment JK de .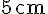

2. À partir du point J, trace un angle de 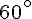en utilisant un rapporteur. Place le point L sur cet angle.

3. À partir du point K, trace un angle de 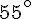en direction du point déjà placé L.

4. Ajuste la position de L pour que les deux angles et le segment JK soient correctement définis. Ensuite, connecte les points L et K pour compléter le triangle JKL.

Construction du cercle circonscrit :

1. Trace les médiatrices des segments JK, JL, et KL.

2. Le point de rencontre des médiatrices est le centre du cercle circonscrit. Appelle ce point O.

3. Utilise un compas placé sur le point O et ajuste-le à la distance OJ, OK ou OL pour dessiner le cercle qui passe par les trois sommets J, K, et L.

Exercice 3 – construction – triangle, bissectrice, hauteur

1) Construction du triangle ABC :

– Tracer le segment .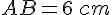

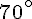
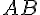
– À partir de A, tracer un angle de avec .

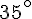
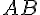
– À partir de B, tracer un angle de avec .

– L’intersection de ces deux angles détermine le point C.

2) Construction de la bissectrice de l’angle 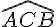\(\widehat{ACB}\) :

– Utiliser un rapporteur pour mesurer l’angle 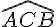\(\widehat{ACB}\).

– Diviser cet angle en deux parties égales en traçant la bissectrice.

3) Construction de la hauteur issue de A :

– Tracer une perpendiculaire à 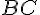passant par le point A. Ceci est la hauteur issue de A.

Exercice 4 – cercle circonscrit, triangle et médiatrices

Le texte indique que le trésor est enterré à la même distance de la tour T, de l’arbre A et du puits P. Cela signifie que le trésor est situé au centre du cercle circonscrit au triangle formé par les points T, A et P.

Le centre de ce cercle, appelé centre du cercle circonscrit, est le point d’intersection des médiatrices des côtés du triangle.

Pour déterminer l’emplacement exact, il faut tracer les médiatrices des segments [TA], [TP] et [AP] et trouver leur point d’intersection, comme suit :

1. Tracez la médiatrice du segment [TA].

2. Tracez la médiatrice du segment [TP].

3. Le point où ces deux médiatrices se croisent est le centre du cercle circonscrit. Ce sera l’emplacement du trésor.

De manière générale, pour trois points non alignés, le centre du cercle circonscrit est unique.

Exercice 5 – somme des angles d’un triangle

1. Triangle LNI :

On sait que la somme des angles d’un triangle est de .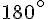

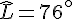
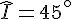
On a les angles : et .

On calcule :

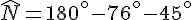
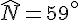
2. Triangle SAC :

La somme des angles d’un triangle est .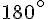

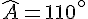
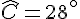
On a les angles : et .

On calcule :

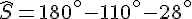
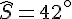
Exercice 6 – géographie et somme des angles d’un triangle.

Pour trouver la mesure de l’angle notée , nous devons utiliser la propriété que la somme des angles d’un triangle est de 180 °.

Nous avons les angles suivants dans le triangle :

• L’angle de la tour :  84,7 °
• L’angle avec le fil à plomb : 90 °
• La valeur  que nous devons trouver.

Donc, nous pouvons écrire l’équation :

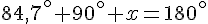
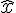
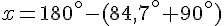
En isolant , nous obtenons :

Donc :

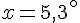
Conclusion : La mesure de l’angle est donc  5,3 °.

1. Calcul de l’angle :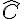

Dans le triangle ABC, la somme des angles est égale à 180°. Ainsi :

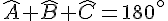
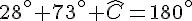
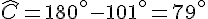
2. Calcul de l’angle :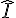

Dans le triangle GHI, étant donné que le triangle est rectangle en H :

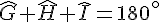
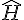
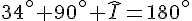
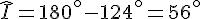
On sait que =90 ° :

3. Calcul des angles et :

Dans le triangle isocèle MNO, = :

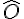
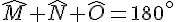
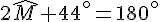
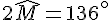
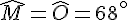
4. Mesures des angles de la figure :

En utilisant la figure et ses indications :

– Triangle ABD :

– Avec , donc .

– Triangle CDB : rectangle en D, donc et .

– Triangle CED : est également isocèle, donc et .

Exercice 8 – triangle, hauteur, médiatrices, bissectrices et médianes.

a) Hauteur issue de A :

Tracer la hauteur issue de A en vert, perpendiculaire à la base [BC].

b) Médiane passant par B :

Tracer la médiane en bleu reliant B au milieu du segment [AC].

c) Bissectrice de l’angle ACB :

Tracer la bissectrice en noir de l’angle ACB, coupant cet angle en deux angles égaux.

d) Médiatrice du segment [BC] :

Tracer la médiatrice en rouge du segment BC, perpendiculaire et passant par le milieu de BC.

e) Calcul de la mesure de l’angle ACB :

Utiliser la somme des angles dans un triangle :

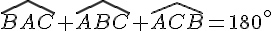
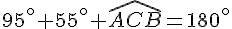
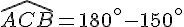
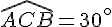
Exercice 9 – calculer la mesure d’un angle.

Pour déterminer la mesure de l’angle , nous devons utiliser les propriétés des parallélogrammes.

Étape 1 : Dans le parallélogramme ABCD, les angles opposés sont égaux.

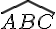
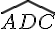
Donc, l’angle est égal à 105°, et par conséquent l’angle est également égal à 105°.

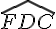
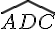
Étape 2 : Puisque (AD) est parallèle à (CF) et que (DF) est une sécante entre ces deux parallèles, l’angle est égal à l’angle , qui est 105°.

Étape 3 : L’angle est un angle supplémentaire à l’angle , où D + = 180°.

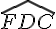
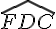
Calcul :

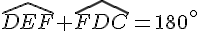
En substituant la valeur de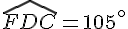

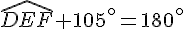
Résolution de l’équation :

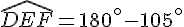
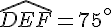
Conclusion : La mesure de l’angle est

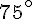
Exercice 10 – calcul de la mesure d’un angle.

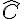
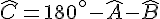
Dans un triangle, la somme des angles est toujours égale à 180°. Ainsi, pour trouver la mesure de l’angle , nous utilisons la formule suivante :

En remplaçant par les valeurs données :

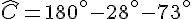
Calculons :

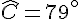
La mesure de l’angle est donc de 79°.