Volumes : corrigé des exercices de maths en 4ème en PDF

Mis à jour le 23 novembre 2025

Dans l’apprentissage des maths en quatrième, la compréhension des volumes est cruciale. Cette notion permet aux élèves de développer des compétences essentielles, telles que le calcul de l’espace occupé par des objets, et d’améliorer leur raisonnement logique. À travers des exercices corrigés, cet article vise à renforcer ces acquis et à préparer efficacement les élèves aux futurs défis mathématiques.

Exercice 1 – calcul du volume d’un cône de révolution

Objectif : Calculer le volume d’un cône de révolution.

Le volume V d’un cône est donné par la formule :

$V=\frac{1}{3}\pi R^2h$

où :

R est le rayon de la base du cône.
h est la hauteur du cône.

Dans cet exercice, nous avons :

Rayon R = 5 cm} .
Hauteur h = 6 cm.

En substituant ces valeurs dans la formule, nous obtenons :

$V=\frac{1}{3}\pi\times 5^2 \times 6$

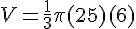
$V=\frac{1}{3}\pi(25)(6)$

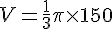
$V=\frac{1}{3}\pi\times150$

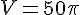
$V=50\pi$

Donc, le volume du cône est 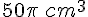$50\pi\,cm^3$ .

Exercice 2 – calcul du volume d’une pyramide.

Pour calculer le volume d’une pyramide, on utilise la formule :

$V=\frac{1}{3}\times B\times h$

où B est l’aire de la base et h est la hauteur de la pyramide.

Étape 1 : Calcul de l’aire de la base.

La base est un rectangle de dimensions 30 m et 50 m.

$B=30\times 50=1500\ m^2$

Étape 2 : Calcul du volume de la pyramide.

La hauteur de la pyramide est de 90 m.

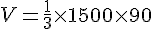
$V=\frac{1}{3}\times1500\times90$

$V=45000\ m^3$

Conclusion :

Le volume de la pyramide est de 45 000 m³.

Exercice 3 – patron d’un cône de révolution.

1. Quel est le sommet de ce cône ?

Le sommet du cône est le point qui n’appartient pas au disque de base, situé à l’extrémité opposée à la base.

2. Quel est le centre et le rayon de son disque de base ?

Le centre du disque de base est l’origine du cercle de base, et le rayon est la distance entre le centre et n’importe quel point du bord du cercle.

3. Quelle est la longueur d’une génératrice ?

La génératrice est le segment qui relie le sommet du cône à un point du cercle de base. Si on connaît le rayon et la hauteur du cône, la longueur de la génératrice est donnée par :

$g=\sqrt{r^2+h^2}$

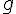
4. Calculer la longueur de l’arc de cercle BC.

La longueur de l’arc de cercle BC est trouvée à partir de l’angle au sommet 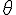$\theta$ en radians et le rayon de l’arc (génératrice) :

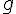
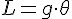
$L=g\cdot\theta$

Exercice 4 – pyramide droite à base rectangulaire.

1. Quelle est la nature de BCDE ?

BCDE est un rectangle.

2. Quelle est la hauteur de ABCDE ?

La hauteur de la pyramide ABCDE est le segment [AD].

Pour la trouver, utilisons le théorème de Pythagore dans le triangle rectangle ABE :

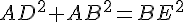
$AD^{2}+AB^{2}=BE^{2}$

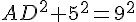
$AD^{2}+5^{2}=9^{2}$

$AD^{2}+25=81$

$AD^{2}=56$

$AD=\sqrt{56}$

Soit 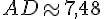$AD\approx7,48$ cm.

3. Tracer en vraie grandeur le triangle ABC.

Pour tracer le triangle ABC, utilisez les longueurs : AB = 5 cm, BC = 7 cm, et AC déterminé par le théorème de Pythagore :

Dans le triangle rectangle ABC :

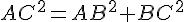
$AC^{2}=AB^{2}+BC^{2}$

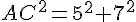
$AC^{2}=5^{2}+7^{2}$

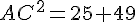
$AC^{2}=25+49$

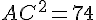
$AC^{2}=74$

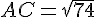
$AC=\sqrt{74}$

Soit 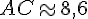$AC\approx8,6$ cm.

Tracez le triangle avec les longueurs précises de AB = 5 cm, BC = 7 cm, et AC ≈ 8,6 cm.

Exercice 5 – volume d’une pyramide à base carrée.

Le volume d’une pyramide est donné par la formule :

$V=\frac{1}{3}\times B\times h$

Où B est l’aire de la base et h est la hauteur de la pyramide.

Calcul de l’aire de la base :

La base est un carré de côté 6 cm, donc :

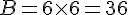
$B=6\times6=36$

Calcul du volume :

La hauteur de la pyramide est 34 cm.

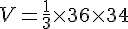
$V=\frac{1}{3}\times36\times34$

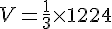
$V=\frac{1}{3}\times1224$

V=408

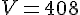
Le volume de la pyramide est $408\ cm^3$ .

Exercice 6 – volume d’une cône de révolution.

Le volume V d’un cône est donné par la formule :

$V=\frac{1}{3}\pi r^2 h$

Où :

r = 7 cm est le rayon de la base
h = 9 cm est la hauteur

En substituant les valeurs :

$V=\frac{1}{3}\pi \times (7)^2 \times 9$

Calculons :

$V=\frac{1}{3}\times \pi \times 49 \times 9$

$V=\frac{441}{3}\times \pi$

$V=147\pi$

Approximativement :

$V\approx 147\times 3,14$

$V\approx 461,58\,\text{cm}^3$

Donc, le volume du cône est d’environ 461,58 cm³.

Exercice 7 – volume d’une pyramide à base triangulaire.

1. Calcul de l’aire de la base :

La base de la pyramide est un triangle rectangle en B. La formule pour l’aire d’un triangle rectangle est :

$Aire=\frac{1}{2}\times AB\times BC$

Ici, AB=4,5 et BC=6 , donc :

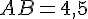
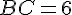
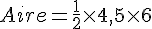
$Aire=\frac{1}{2}\times4,5\times6$

$Aire=13,5\ cm^2$

2. Calcul du volume de la pyramide :

La formule pour le volume d’une pyramide est :

$Volume=\frac{1}{3}\times Aire\times hauteur$

Avec une hauteur de $7\ cm$ , le volume est :

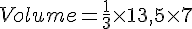
$Volume=\frac{1}{3}\times13,5\times7$

$Volume=31,5\ cm^3$

Exercice 8 – volume d’une pyramide à base un parallèlogramme.

Pour calculer le volume de la pyramide, nous devons d’abord calculer l’aire de la base, qui est un parallélogramme.

L’aire A d’un parallélogramme est donnée par la formule :

$A=b\times h$

Où b est une base du parallélogramme et h est la hauteur correspondante. Dans cet exercice :

b = AB = 4 cm
h = AH = 4 cm

Donc, l’aire de la base est :

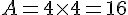
$A=4\times4=16$ cm²

Le volume V de la pyramide est donné par :

$V=\frac{1}{3}\times \text{Aire\ de\ la\ base}\times \text{Hauteur\ de\ la\ pyramide}$

Avec une hauteur de pyramide de 8 cm, nous avons :

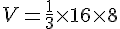
$V=\frac{1}{3}\times16\times8$

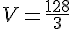
$V=\frac{128}{3}$

Le volume de la pyramide est $\frac{128}{3}\approx42,67$ cm³.

Exercice 9 – calcul du rayon de la base d’un cône.

Le volume V d’un cône de révolution est donné par la formule :

$V=\frac{1}{3}\pi r^2 h$

On connaît le volume 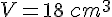$V=18\,cm^3$ et la hauteur h = 5 cm.

Nous devons trouver le rayon r .

En remplaçant les valeurs, nous avons :

$18=\frac{1}{3}\pi r^2 \times 5$

En simplifiant, cela devient :

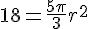
$18=\frac{5\pi}{3}r^2$

Pour isoler r :

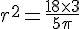
$r^2=\frac{18\times3}{5\pi}$

$r^2=\frac{54}{5\pi}$

En prenant la racine carrée :

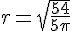
$r=\sqrt{\frac{54}{5\pi}}$

Valeur exacte : 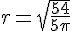$r=\sqrt{\frac{54}{5\pi}}$

Valeur approchée : $r\approx 1,85\,cm$

Exercice 10 – calcul de la hauteur d’une pyramide.

Données :

Volume de la pyramide : $63\ \text{cm}^3$

Base carrée de côté : $5\ \text{cm}$

Formule du volume d’une pyramide :

$V=\frac{1}{3}\times \text{Aire de la base} \times \text{Hauteur}$

Aire de la base carrée :

Aire = $5\ \text{cm} \times 5\ \text{cm} = 25\ \text{cm}^2$

Calcul de la hauteur :

Équation : $63=\frac{1}{3}\times 25 \times \text{Hauteur}$

Donc, $63=\frac{25}{3} \times \text{Hauteur}$

Hauteur 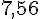= $\frac{63 \times 3}{25}$

Hauteur ≈ 7,56 cm

4.9/5 - (35779 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «volumes : corrigé des exercices de maths en 4ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 759 949 cours et exercices de maths téléchargés en PDF et 4 250 exercices.