Rotation : corrigé des exercices de maths en 4ème en PDF

Exercice 1 – hexagone et rotation.

a. La rotation d’angle 60° autour du point O transforme le triangle AOB en triangle BOA.

Le triangle obtenu est donc BOC.

b. La rotation d’angle 240° correspond à quatre fois la rotation de 60° (car  240°= 4 x 60°).

Donc, la transformation de AOB devient :

.

Le triangle obtenu est donc DOE.

c. La translation qui transforme C en D est une translation d’une unité le long de l’hexagone. Le triangle CED devient DFE par cette translation.

a. On considère la rotation de centre O, d’angle 60° dans le sens inverse des aiguilles d’une montre.

Image du point A :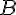

Image du point F :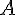

Image du triangle OBA :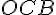

Image du losange ODEF :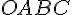

b. On considère la rotation de centre C, d’angle 60° dans le sens des aiguilles d’une montre.

Image du point B :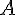

Image du point A :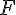

Image du triangle OBA :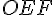

Image du losange OABC :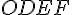

Exercice 3 – image par la rotation de centre O.

a. Construction de A’ et D’

A’ est l’image de A par une rotation de centre O et d’angle 70° dans le sens inverse des aiguilles d’une montre.

D’ est l’image de D par la même rotation.

b. Construction de B’, C’ et E’

B’ est l’image de B par une rotation de centre O et d’angle 45° dans le sens des aiguilles d’une montre.

C’ est l’image de C par la même rotation.

E’ est l’image de E par la même rotation.

c. Décrire la rotation :

Pour que C’ soit l’image de D’ :

Il faut une rotation de centre O d’angle :

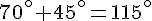
Pour que B’ soit l’image de A’ :

Il suffit de faire une rotation de centre O d’angle :

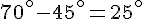
Exercice 4 – l’image d’un quadrilatère.

a. Rotation de centre B, angle 75° (sens inverse) :

Pour construire l’image du quadrilatère ABCD par une rotation de 75° dans le sens inverse des aiguilles d’une montre autour de B, il faut :

• Utiliser un rapporteur pour mesurer un angle de 75° à partir de chaque point A, C et D, en prenant B comme centre de rotation.
• Tracer un arc à 75° à partir de chaque point pivoté.
• Mesurer la même distance de B à chaque sommet (A, C, D) sur les arcs tracés pour déterminer les nouvelles positions des sommets après la rotation.

b. Rotation de centre O, angle 100° (sens des aiguilles d’une montre) :

Pour construire l’image du quadrilatère ABCD par une rotation de 100° dans le sens des aiguilles d’une montre autour de O, il faut :

• Utiliser un rapporteur pour mesurer un angle de 100° à partir de chaque point A, B, C et D, en prenant O comme centre de rotation.
• Tracer un arc à 100° à partir de chaque point pivoté.
• Mesurer la même distance de O à chaque sommet (A, B, C, D) sur les arcs tracés pour déterminer les nouvelles positions des sommets après la rotation.

Exercice 5 – l’image d’un carré.

a. L’image du carré ABCD par la rotation de centre D et d’angle 45° dans le sens inverse des aiguilles d’une montre est le carré A’B’C’D’ (en rouge). Chaque sommet est déplacé de 45° autour de D.

b. L’image du carré ABCD par la rotation de centre A et d’angle 135° dans le sens inverse des aiguilles d’une montre est le carré A »B »C »D » (en vert). Chaque sommet tourne de 135° autour de A.

c. Pour passer du carré noir au carré vert avec une rotation de centre A, on a déjà tourné de 45° en rouge et de 135° pour le vert, donc l’angle total est :

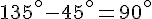
Il faut donc une rotation de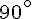

d. L’image du carré ABCD par la rotation de centre I et d’angle 280° dans le sens inverse des aiguilles d’une montre est le carré A »’B »’C »’D »’ (en bleu). Chaque sommet est tourné de 280° autour de I.

Exercice 6 – rotation et symétrie.

a. L’image F₁ de F par la rotation de centre B et d’angle 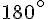est située de l’autre côté de B par rapport à F, à la même distance de B. Elle est obtenue par symétrie centrale par rapport au point B.

b. L’image F₂ de F₁ par la rotation de centre C et d’angle 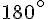est située de l’autre côté de C par rapport à F₁, à la même distance de C.

c. La transformation qui permet de passer de F à F₂ est une translation. En utilisant les points du dessin, cette translation est définie par la composition de deux symétries centrales : d’abord par rapport à B, suivie par une symétrie centrale par rapport à C.

Exercice 7 – déterminer le centre et l’angle d’une rotation.

Étape 1 : Pour déterminer le centre de rotation, on doit trouver le point qui est équidistant de tous les sommets des deux triangles correspondants après rotation.

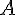
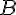
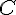
Étape 2 : Une méthode consiste à tracer les médiatrices des segments reliant chaque couple de points corrélatifs (par exemple, de \(A\) à \(A’\), de \(B\) à \(B’\), et de \(C\) à \(C’\)). Le point d’intersection de ces médiatrices sera le centre de rotation.

Étape 3 : Pour déterminer l’angle de rotation, on mesure l’angle formé par un segment original et son image. Par exemple, mesurer l’angle \(\angle(AOC)\) où 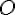\(O\) est le centre de rotation.

Conclusion : Avec le centre 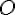\(O\) trouvé précédemment et l’angle mesuré, cela complète la détermination du centre et de l’angle de la rotation.

Exercice 8 – construire les images de points par rotation.

a. Pour construire A’, B’, C’, D’, et E’, on applique une rotation de 60° autour du centre O dans le sens inverse des aiguilles d’une montre. Chaque image de point sera à la même distance de O que le point d’origine, mais déplacée de 60° autour de O.

b. Puisque A et B sont sur le cercle de centre O, leurs images A’ et B’ après une rotation de 60° seront également sur ce cercle. L’angle entre OA et OA’ est de 60°, et l’angle entre OB et OB’ sera également de 60°.

c. Comme C et E appartiennent à la droite (OA), leurs images C’ et E’ seront également alignées avec l’image du point A, qui est A’. L’alignement est conservé, et ainsi C’, O, et A’ restent colinéaires.

Exercice 9 – démonstration en géométrie.

a. Construis A’, B’, C’, D’ et E’ :

Une rotation de 60° dans le sens inverse des aiguilles d’une montre autour de O fera tourner chaque point sur le cercle de centre O dans cet ordre. Pour construire les images :

• A’ est obtenu en tournant A de 60° autour de O.
• B’ est obtenu en tournant B de 60° autour de O.
• C’ est obtenu en tournant C de 60° autour de O.
• D’ est obtenu en tournant D de 60° autour de O.
• E’ est obtenu en tournant E de 60° autour de O.

b. Que peux-tu dire des images de A et B ?

Les points A et B étant sur le cercle centré en O, leurs images A’ et B’ sont aussi sur le cercle, à une distance égale de O. La mesure des arcs ∠AOA’ et ∠BOB’ est alors de 60°.

c. Que peux-tu dire de leurs images ?

Les points C et E appartenant à la droite (OA), subissent la même rotation, formant un angle de 60°. Donc leurs images C’ et E’ seront aussi alignées après rotation, formant un angle de 60° par rapport à C et E, respectivement.

Exercice 10 – construire l’image d’un poisson.

a. Construction avec le compas :

Pour construire l’image du poisson par une rotation de centre O et d’angle 60° dans le sens inverse des aiguilles du montre, en utilisant uniquement le compas :

• Place la pointe du compas sur le point O et trace un cercle passant par un des sommets du poisson.
• Avec le même écartement du compas, place la pointe sur ce sommet et marque un arc de 60° sur le cercle.
• Réitère cette opération pour chaque sommet du poisson.
• Relie les nouveaux points pour obtenir le poisson tourné en rouge.

b. Construction avec l’équerre :

Pour construire l’image du poisson par une rotation de centre O et d’angle 90° dans le sens inverse des aiguilles du montre, en utilisant uniquement l’équerre :

• Utilise l’équerre pour tracer un angle droit (90°) à partir de O vers chaque sommet du poisson.
• Marque les nouveaux sommets en suivant la ligne tracée par l’équerre.
• Relie les nouveaux sommets pour obtenir l’image du poisson en vert.