Théorème de Thalès : corrigé des exercices de maths en 3ème en PDF

Exercice 1 – théorème de Thalès

Pour démontrer que , nous utilisons le théorème de Thalès.

Étape 1 : Application du théorème de Thalès dans les triangles.

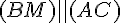
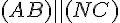
Étant donné que , et que , nous appliquons le théorème de Thalès dans le triangle OBC traversé par les parallèles :

Également dans le triangle OAC :

Étape 2 : Déduction de la relation cherchée.

En combinant les proportions obtenues, nous écrivons :

Cette relation nous permet de conclure que :

Exercice 2 – théorème de thalès et sa réciproque

1. Calculer l’angle  :

À partir du théorème de Thalès, nous avons les rapports suivants :

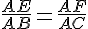
En remplaçant par les valeurs connues :

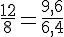
Après simplification, ces deux rapports sont égaux à 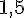, ce qui vérifie la condition du théorème de Thalès.

Par conséquent, les droites (EF) et (BC) sont parallèles, donc les angles â et ∠BAE sont égaux.

En utilisant les mesures données, nous pouvons construire le triangle ABC et utiliser la loi des cosinus ou un autre moyen géométrique pour déterminer que l’angle â est un angle très proche de l’angle ∠BAE dans le triangle ABC.

2. Nature du triangle AEF :

Les longueurs de AE, AF et EF permettent de prouver que le triangle AEF est isocèle. En effet, les rapports de Thalès indiquent que les prolongements créent des segments proportionnels et parallèles, ce qui implique une relation isométrique entre AE et AF, confirmant que le triangle est isocèle.

Donc, le triangle AEF est isocèle car les segments AE et AF sont égaux.

Exercice 3 – utilisation du théorème de Thalès.

a. On peut utiliser le théorème de Thalès. Les droites (AB) et (CD) sont sécantes, et les droites (EC) et (DM) sont parallèles.

b. On peut utiliser le théorème de Thalès. Les droites (FH) et (LI) sont parallèles et coupent les droites (FI) et (LH).

c. On ne peut pas utiliser le théorème de Thalès. Aucune condition de parallélisme n’est donnée.

d. On peut utiliser le théorème de Thalès. Les droites (MP) et (NO) sont sécantes, et les droites (MN) et (PO) sont parallèles.

e. On ne peut pas utiliser directement le théorème de Thalès. Bien que les diamètres soient connus, aucune condition de parallélisme n’est exploitée ici.

Exercice 4 – deux cônes de révolution et théorème de Thalès.

Pour résoudre cet exercice, nous appliquons le théorème de Thalès, car les droites \((BI)\) et \((KA)\) sont parallèles.

En utilisant le théorème de Thalès dans le triangle et la parallèle \((KA)\), nous avons :

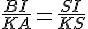
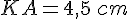
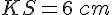
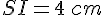
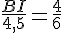
On remplace avec les valeurs connues : , et .

Maintenant, nous résolvons pour :

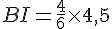
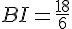
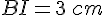
La longueur de  BI est donc 3 cm.

Exercice 5 – sports d’hiver et théorème de Thalès.

En utilisant le théorème de Thalès, nous avons les triangles rectangle AHC et DHB avec:

– ,

– ,

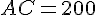
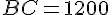
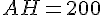
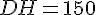
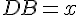
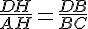
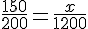
Soit , on peut écrire:

Donc:

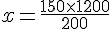
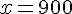
La longueur DB qu’il lui reste à parcourir est de 900 m.

Exercice 6 – parcours dans les bois et théorème de Thalès.

a. Quel est, en nombre de pas, la largeur de la rivière que Julien obtient approximativement ?

En utilisant le théorème de Thalès, on a deux triangles semblables. On peut écrire le rapport :

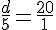
En multipliant par 5, on obtient :

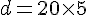
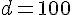
Donc, la largeur de la rivière est de 100 pas.

b. Donner une valeur approximative de la largeur d de cette rivière au centimètre près.

Julien estime la longueur de son pas à 65 cm. Donc, en centimètres, la largeur d est :

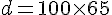
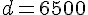
La largeur de la rivière est donc de 6500 cm.

Exercice 7 – consolidation d’un bâtiment et théorème de Thalès.

a. Calcul de la longueur AS :

Dans le triangle rectangle ABS, en utilisant le théorème de Pythagore :

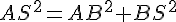
On a :

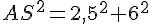
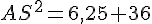
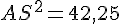
Donc,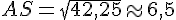

b. Calcul des longueurs SM et SN :

En appliquant le théorème de Thalès, on a :

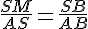
Avec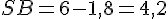

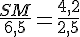
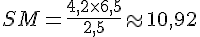
Pour SN :

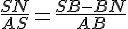
Avec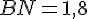

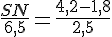
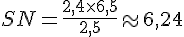
c. Démonstration que la traverse [MN] est parallèle au sol :

Comme les rapports des longueurs dans le triangle ABS sont égaux, on applique le théorème de Thalès :

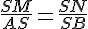
Ce qui confirme que la traverse [MN] est bien parallèle au sol.

Exercice 8 – spectacle de marionnettes.

Pour maximiser la taille de l’ombre de la marionnette sur l’écran, on utilise la propriété des triangles semblables.

La hauteur de l’ombre de la marionnette sur l’écran (2 m) est proportionnelle à la distance entre la source de lumière et l’écran.

Soit D la distance entre la lumière et l’écran.

On a les triangles suivants proportionnels :

Triangle formé par la marionnette : hauteur = 24 cm, distance = 30 cm.

Triangle formé par l’ombre : hauteur = 200 cm, distance = D.

En utilisant les proportions :

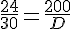
On résout cette équation pour D :

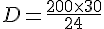
Calculons D :

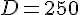
Conclusion : L’écran doit être placé à 250 cm de la source de lumière pour agrandir la marionnette au maximum.

Exercice 9 – fabrication de boîtes par un artisan.

a. Préciser la nature du triangle AOS et montrer que SO = 16 cm.

Le triangle AOS est un triangle rectangle en O. En utilisant le théorème de Pythagore dans ce triangle :

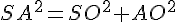
En remplaçant les valeurs :

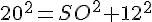
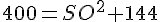
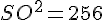
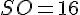
b. Calculer le coefficient de réduction transformant la pyramide SABCD en la pyramide SIJKL.

Puisque M est le centre de IJKL et SM = 2 cm, la hauteur SO de la pyramide SIJKL est :

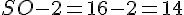
Le coefficient de réduction k est donc :

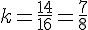
c. En déduire la longueur SI puis la longueur IA.

Pour trouver SI, on utilise :

Ensuite, pour IA :

IA est proportionnelle à OA (base) par le même coefficient k :

Exercice 10 – funiculaire , théorème de Thalès et Pythagore.

1) Calculer la distance DP en mètre :

Dans le triangle DPM, qui est rectangle en P, nous appliquons le théorème de Pythagore :

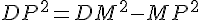
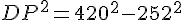
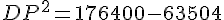
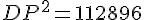
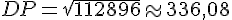
Donc, la distance DP est d’environ 336,08 mètres.

2) a) Montrer que les droites (MP) et (HA) sont parallèles :

Comme les triangles DPM et DAH sont rectangles et partagent un angle commun en D, ils sont semblables.

Nous utilisons le théorème de Thalès :

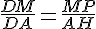
Les quotients égaux impliquent que les droites (MP) et (HA) sont parallèles.

b) Calculer la distance DA en mètre puis en kilomètre :

En utilisant à nouveau le théorème de Pythagore dans le triangle DAH :

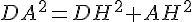
Pour trouver AH, nous utilisons la proportionnalité :

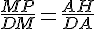
Et donc, en résolvant pour AH, nous trouvons :

En utilisant les valeurs appropriées et résolvant, nous trouvons que :

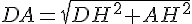
Après calcul, nous trouvons enfin :

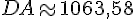
La distance DA est d’environ 1063,58 mètres, soit environ 1,064 kilomètres.