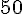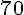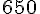Problèmes et calculs : corrigé des exercices de maths en CM2 en PDF

Mis à jour le 23 novembre 2025

Les exercices de mathématiques en CM2 jouent un rôle crucial dans le développement des compétences des élèves. Face aux défis des problèmes et calculs, il est essentiel de maîtriser des notions fondamentales telles que l’addition, la soustraction, la multiplication et la division. En travaillant sur ces exercices, les élèves renforcent leur logique et leur raisonnement, préparant ainsi le terrain pour des apprentissages futurs. Cet article propose des corrections détaillées pour aider les élèves à progresser et à surmonter leurs difficultés.

Exercice 1 – un lombricomposteur de jardin.

a. Masse des lombrics :

La population des lombrics double tous les trois mois. En un an (12 mois), il y a donc 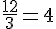$\frac{12}{3}=4$ périodes de trois mois.

La population sera multipliée par 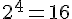$2^{4}=16$ . Par conséquent, la masse sera multipliée par 16.

La masse initiale étant de 500 g :

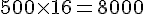
$500\times 16=8000$

La masse des lombrics après un an est de 8000 g, soit 8 kg.

b. Nombre de lombrics :

Le nombre initial de lombrics est de 1000. Comme la population double tous les trois mois et qu’il y a 4 périodes de trois mois en un an :

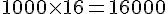
$1000\times 16=16000$

Le nombre de lombrics après un an est de 16 000.

Exercice 2 – des champignons microscopiques.

a. Quantités pour 75 m² :

Pour 30 m², il faut 50 g d’ail et 650 g d’oignons. Pour 75 m², on effectue un produit en croix.

Ail :

$\frac{50}{30}\times 75=125$ g d’ail

Oignons :

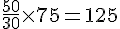
$\frac{650}{30}\times 75=1625$ g d’oignons

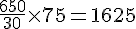
b. Aire maximale avec 150 g d’ail et 2 kg d’oignons :

Pour 50 g d’ail, on traite 30 m². Pour 150 g :

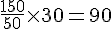
$\frac{150}{50}\times 30=90$ m²

Pour 650 g d’oignons, on traite 30 m². Pour 2000 g (2 kg) :

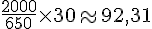
$\frac{2000}{650}\times 30\approx92,31$ m²

La quantité limitée est celle de l’ail. Zolan peut donc traiter 90 m².

Exercice 3 – problème du potager.

a. Pour les pommes de terre :

Coût d’achat : 7 €.

Quantité récoltée : 30 kg.

Prix en magasin : 1,60 € le kg.

Économie réalisée :

Valeur des pommes de terre en magasin :

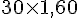
$30\times 1,60$ = 48 €

Économie :

= 41 €

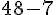
b. Calcul pour chaque légume :

Pour les tomates :

Coût des graines : 7,50 €

Quantité récoltée : 6,5 kg

Valeur en magasin :

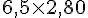
$6,5\times 2,80$ = 18,20 €

Économie :

= 10,70 €

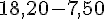
Pour les carottes :

Coût des graines : 7,50 €

Quantité récoltée : 20 kg

Valeur en magasin :

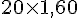
$20\times 1,60$ = 32 €

Économie :

= 24,50 €

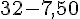
Pour les haricots :

Coût des graines : 7,50 €

Quantité récoltée : 1 kg

Valeur en magasin :

5 €

Économie :

= -2,50 €

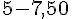
Pour les laitues :

Coût des graines : 7,50 €

Quantité récoltée : 15 unités

Valeur en magasin :

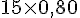
$15\times 0,80$ = 12 €

Économie :

= 4,50 €

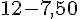
Pour les courgettes :

Coût des graines : 7,50 €

Quantité récoltée : 10 unités

Valeur en magasin :

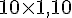
$10\times 1,10$ = 11 €

Économie :

= 3,50 €

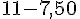
Exercice 4 – problème du verger.

a. Combien de Français possèdent un jardin ?

63 % de 60 millions, soit $0,63\times 60\ 000\ 000$ = 37,8 millions.

b. Combien de Français cultivent un potager ou un verger ?

67 % de ceux qui possèdent un jardin, donc $0,67\times 37,8\ 000\ 000$ = 25,326 millions.

Cela représente moins que la moitié de la population française puisque 30 millions serait la moitié.

c. Combien de Français cultivent uniquement un potager ? Uniquement un verger ? Les deux ?

Uniquement un potager : $0,37\times 25,326\ 000\ 000$ = 9,366 millions.

Uniquement un verger : $0,38\times 25,326\ 000\ 000$ = 9,621 millions.

Les deux : $0,25\times 25,326\ 000\ 000$ = 6,3315 millions.

Exercice 5 – problème du trou.

Réponse a :

Pour réaliser un plan de dessus et un plan de coupe à l’échelle 1:10 du trou :

– Plan de dessus :

La partie supérieure est un pavé droit de dimensions 1,60 m × 1,60 m × 0,30 m.

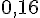
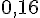
À l’échelle 1:10, les dimensions seront : m × m.

– Plan de coupe :

Le trou est composé de deux parties : un cube de côté 0,90 m et un pavé droit de 1,60 m × 1,60 m × 0,30 m.

À l’échelle 1:10 :

La hauteur du cube : 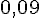m.

La hauteur du pavé droit : 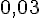m.

Réponse b :

Calculons le volume total du trou :

– Volume du cube : 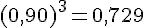m³.

– Volume du pavé droit : 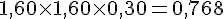$1,60\times 1,60\times 0,30=0,768$ m³.

Volume total : 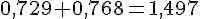m³.

Convertissons ce volume en litres :

– 1 m³ = 1000 L

– Volume total en litres : 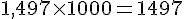$1,497\times 1000=1497$ L.

Nombre de seaux de 3 L :

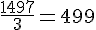
$\frac{1497}{3}=499$

Nombre total de seaux : 499 seaux.

Exercice 6 – problème de l’appartement.

L’appartement qui correspond aux attentes de Zolan et Chama est l’Appart. A3 avec 2 chambres, une superficie de 50 m² et un prix de 610 €.

Justification :

L’appartement doit avoir au moins 2 chambres.
La superficie doit être comprise entre m² et m².
Le prix doit être inférieur ou égal à €.

Analyse des options :

Appart. A1 : 70 m², 2 chambres, 660 € (trop cher).
Appart. A2 : 56 m², 1 chambre (pas assez de chambres).
Appart. A3 : 50 m², 2 chambres, 610 € (correspond à toutes les attentes).
Appart. A4 : 58 m², 1 chambre (pas assez de chambres).
Appart. A5 : 85 m² (trop grand), 3 chambres, 520 €.
Appart. A6 : 64 m², 2 chambres, 1 200 € (trop cher).

Exercice 7 – nombre de bébés nommés Ruby.

a. Complète le diagramme en barres :

Complétez le diagramme en reportant les valeurs de chaque année sur l’axe vertical. Chaque barre doit correspondre au nombre de bébés nommés Ruby pour l’année spécifiée.

b. Décris l’évolution du nombre de bébés se prénomment Ruby au cours de ces années :

Entre 1988 et 1999, le nombre de bébés nommés Ruby varie autour d’une dizaine, atteignant un pic de 17 en 1997. À partir de 2000, une augmentation significative est observée, culminant à 46 en 2007. Après 2007, le nombre diminue à nouveau, mais reste élevé comparé aux années précédentes, avec 34 en 2010.

Exercice 8 – le biberon de lait.

a. Complétion de la troisième colonne :

Cette colonne est proportionnelle. On observe que :

Pour 90 mL, il y a 3 mesurettes de lait, donc pour 1 mL, il y a 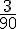$\frac{3}{90}$ mesurettes de lait.

Alors, pour 120 mL : 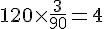$120\times \frac{3}{90}=4$ mesurettes.

Pour 150 mL : 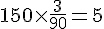$150\times \frac{3}{90}=5$ mesurettes.

Pour 180 mL : 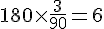$180\times \frac{3}{90}=6$ mesurettes.

Pour 210 mL : 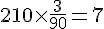$210\times \frac{3}{90}=7$ mesurettes.

Pour 240 mL : 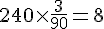$240\times \frac{3}{90}=8$ mesurettes.

b. Quantité totale d’eau pour 6 mois :

Pour chaque tranche d’âge, on calcule la consommation en eau par mois :

– 0 à 1 mois : 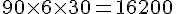$90\times 6\times 30=16200$ mL.

– 1 à 2 mois : 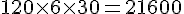$120\times 6\times 30=216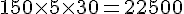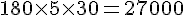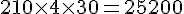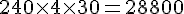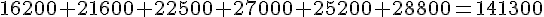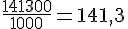00$ mL.

– 2 à 3 mois : $150\times 5\times 30=22500$ mL.

– 3 à 4 mois : $180\times 5\times 30=27000$ mL.

– 4 à 5 mois : $210\times 4\times 30=25200$ mL.

– 5 à 6 mois : $240\times 4\times 30=28800$ mL.

Total : mL.

En litres : $\frac{141300}{1000}=141,3$ litres.

c. Nombre total de mesurettes de lait :

Pour chaque tranche d’âge, calculons le nombre de mesurettes par mois :

– 0 à 1 mois : 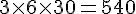$3\times 6\times 30=540$

– 1 à 2 mois : 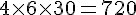$4\times 6\times 30=720$

– 2 à 3 mois : 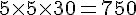$5\times 5\times 30=750$

– 3 à 4 mois : 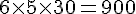$6\times 5\times 30=900$

– 4 à 5 mois : 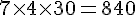$7\times 4\times 30=840$

– 5 à 6 mois : 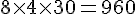$8\times 4\times 30=960$

Total : 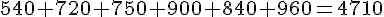mesurettes.

Exercice 9 – couches jetables et lavables.

a. Pour 750 000 enfants, la consommation de couches jetables est de :

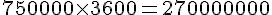
$750000\times 3600=270000000$

Masse totale des déchets :

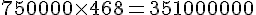
$750000\times 468=351000000$

Coût total de traitement :

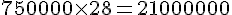
$750000\times 28=21000000$

b. Économie annuelle d’une crèche de 46 enfants :

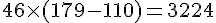
$46\times (179-110)=3224$

Économie sur 2 ans :

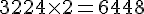
$3224\times 2=6448$

c. Quantité d’électricité consommée par 46 enfants en 2 ans :

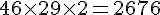
$46\times 29\times 2=2676$

La crèche économise 6448€ et consomme 2676 kWh en 2 ans.

Exercice 10 – des relevés du sommeil.

a. Calcule la durée totale de sommeil de Ruby à 1 semaine et à 3 mois.

Pour 1 semaine :

Sommeil diurne = 1 h 56 + 1 h 47 + 2 h 08 = 5 h 51

Sommeil nocturne = 3 h 12 + 2 h 52 + 3 h 04 = 9 h 08

Durée totale = 5 h 51 + 9 h 08 = 14 h 59

Pour 3 mois :

Sommeil diurne = 2 h 16 + 2 h 42 + 2 h 35 = 7 h 33

Sommeil nocturne = 6 h 18 + 1 h = 7 h 18

Durée totale = 7 h 33 + 7 h 18 = 14 h 51

b. La durée totale de sommeil de Ruby à 6 mois est de 15 h 20. Quelle est la durée de sommeil nocturne de Ruby à 6 mois ?

Sommeil diurne à 6 mois = 2 h 07 + 1 h 57 + 1 h 32 = 5 h 36

Durée totale = 15 h 20

Sommeil nocturne = 15 h 20 – 5 h 36 = 9 h 44

4.8/5 - (32017 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «problèmes et calculs : corrigé des exercices de maths en CM2 en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Gestion de données

Solides de l’espace

Longueur, masse et volume

Durée

Opérations et calculs

Figures et construction

Symétrie axiale

Cercle et triangle

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 331 584 cours et exercices de maths téléchargés en PDF et 4 250 exercices.