Figures et construction : corrigé des exercices de maths en CM2 en PDF
Mis à jour le 23 novembre 2025
Exercice 1 – différents polygones.
Quadrilatère : Fig. H et Fig. I
Pentagone : Fig. C et Fig. G
Hexagone : Fig. F et Fig. J
Heptagone : Fig. D
Octogone : Fig. B
Nonagone : Fig. A
Décagone : Fig. E et Fig. K
Exercice 2 – indiquer la nature du polygone.
a. Ce polygone est un pentagone non convexe car il a cinq côtés et un angle intérieur qui dépasse 180 degrés.
b. Ce polygone est un pentagone non convexe car il a cinq côtés et des côtés qui se croisent.
c. Ce polygone est un quadrilatère convexe car il a quatre côtés et tous les angles sont inférieurs à 180 degrés.
d. Ce polygone est un hexagone convexe car il a six côtés et tous les angles sont inférieurs à 180 degrés.
Exercice 3 – nombre de diagonales d’un polygone.
Formule : Le nombre de diagonales d’un polygone à 
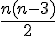
a. Tracé : Tracez toutes les diagonales des polygones donnés en vous basant sur leur nombre de côtés.
b. Complétion du tableau : Utilisez la formule pour calculer le nombre de diagonales de chaque polygone.
| Polygone | Quadrilatère | Pentagone | Hexagone | Heptagone |
|---|---|---|---|---|
| Nombre de diagonales | 
|

|

|

|
Exercice 4 – reproduire l’heptagone.
Pour reproduire l’heptagone MNPQRSTU en vraie grandeur, commencer par tracer le segment MS de 9 cm.
Puis, suivez ces étapes en utilisant les longueurs et les angles donnés :
- Tracez MU = 4,5 cm à partir de M.
- Tracez UN = 3,3 cm en veillant à respecter l’angle droit unit avec U.
- Tracez NNP = 5,2 cm à partir de N.
- Tracez PQ = 4,3 cm à partir de P.
- Tracez SR = 9 – PQ = 4,7 cm pour fermer le polygone avec R.
- Assurez-vous que TS = 3,6 cm complète correctement le chemin pour l’encadrement intérieur de l’heptagone.
Terminez avec les calculs vectoriels appropriés pour vérifier les correspondances des segments et fermer l’heptagone avec précision.
Exercice 5 – classer chaque quadrilatère.
Quadrilatère : Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7, Fig. 8, Fig. 9
Carré : Aucun
Rectangle : Fig. 5
Losange : Fig. 6
Parallélogramme : Fig. 1, Fig. 3, Fig. 9
Quadrilatère quelconque : Fig. 2, Fig. 4, Fig. 7, Fig. 8
Exercice 6 – carré, losange, rectangle et parallélogramme.
a. Les carrés en bleu : Identifiez les formes avec quatre côtés égaux et quatre angles droits.
b. Les rectangles en rouge : Cherchez les quadrilatères avec quatre angles droits mais pas tous les côtés égaux.
c. Les losanges en vert : Trouvez les quadrilatères avec quatre côtés égaux sans nécessairement avoir d’angles droits.
d. Les parallélogrammes en jaune : Repérez les formes avec deux paires de côtés parallèles. Tous les losanges sont des parallélogrammes.
e. Les quadrilatères quelconques en orange : Coloriez les formes restantes qui ne possèdent pas les caractéristiques précédentes.
Exercice 7 – programme de construction.
Figure a :
1. Trace le segment [HW] de 6 cm.
2. Trace un cercle de centre H et de rayon 9,5 cm.
3. Place le point X sur le cercle tel que WX = 9,5 cm} .
4. Complète le parallélogramme en traçant [HV] et [VX].
Figure b :
1. Trace le segment [RP]de 3,4 cm.
2. Trace un angle droit à chaque extrémité de [RP].
3. Prolonge chaque côté et crée un carré en traçant PT = 3,4 cm et RA = 3,4 m .
Figure c :
1. Trace le segment [CS] de 5,8 cm.
2. Trace un angle droit à chaque extrémité de [CS].
3. Prolonge les côtés et crée un rectangle en traçant SF = 4,3 cm .
4. Complète le rectangle en traçant NF = 5,8 cm .
Exercice 8 – droites parallèles et carré.
a. Traçons d’abord les diagonales du carré WXYZ :
- Les diagonales sont (WZ) et (XY).
Ensuite, traçons les droites parallèles demandées :
- La droite parallèle à (WY) passant par X est une ligne horizontale au-dessus de XY.
- La droite parallèle à (WY) passant par Z est une ligne horizontale en dessous de ZX.
- La droite parallèle à (XZ) passant par W est une ligne verticale à gauche de WZ.
- La droite parallèle à (XZ) passant par Y est une ligne verticale à droite de XY.
Ces droites se croisent en formant un nouveau quadrilatère à l’intérieur du carré et un carré plus grand à l’extérieur.
b. Le quadrilatère formé par les intersections externes des droites parallèles est aussi un carré, car les côtés sont parallèles et de même longueur, et les angles sont tous droits.
Exercice 9 – donner un programme de contruction.
Étape 1 : Dessiner le rectangle ABCD tel que AB = 12 \, cm et AD = 5 \, cm.
Étape 2 : Tracer un cercle de centre B et de rayon 3 \, cm.
Étape 3 : Dessiner la diagonale [AC] du rectangle.
Étape 4 : Tracer la perpendiculaire de [AC] passant par A pour atteindre le cercle au point E, puis compléter le quadrilatère AFED.
Exercice 10 – reproduire cette figure.
Étapes pour reproduire et continuer la construction :
1. Reproduisez exactement la figure initiale sur votre feuille quadrillée :
- Observez que la figure occupe une grille de 5×5 cases.
- Chaque forme en « L » est composée de trois carrés verts connectés.
2. Continuez le motif en respectant la symétrie et la continuité :
- Étendez le motif sur les grilles adjacentes en suivant le même pattern.
- Assurez-vous que toutes les lignes formées sont parallèles et équidistantes.
Conseil : Utilisez une règle pour prolonger les lignes si nécessaire.
Télécharger ou imprimer cette fiche «figures et construction : corrigé des exercices de maths en CM2 en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.





