Cercle et triangle : corrigé des exercices de maths en CM2 en PDF

Exercice 1 – notion de diamètre et rayon.

[AM] est un diamètre : oui

[AM] est un rayon : non

[RC] est un diamètre : non

[RC] est un rayon : oui

[IE] est un diamètre : non

[IE] est un rayon : oui

[EM] est un diamètre : non

[EM] est un rayon : oui

[AC] est un diamètre : non

[AC] est un rayon : oui

Exercice 2 – repasser des cercles.

1. Cercle de centre A et de rayon 4 cm (Rouge) :
Le centre A est déjà marqué sur la figure. Repasser le cercle ayant A comme centre et un rayon de 4 cm en rouge.

2. Deux cercles de diamètre 4 cm (Vert) :
– Avec I et J comme centres, on trace deux cercles de diamètre 4 cm. Cela signifie que chaque rayon est de 2 cm. Repasser les cercles en vert.

3. Cercle de diamètre [IB] (Bleu) :
Le diamètre [IB] est la distance entre les points I et B. Repasser le cercle avec un diamètre [IB] en bleu.

4. Cercle de diamètre [CJ] (Noir) :
Le diamètre [CJ] est la distance entre les points C et J. Repasser le cercle avec un diamètre [CJ] en noir.

Exercice 3 – tracer un cercle de centre A.

1. Trace un cercle de centre A et de rayon 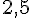cm.

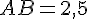
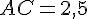
2. Trace deux rayons en bleu. Un rayon est un segment reliant le centre A à un point du cercle. Par exemple, trace les segments [AB] et [AC] tels que cm et cm.

3. Trace deux diamètres en rouge. Un diamètre est un segment passant par le centre et reliant deux points du cercle. Par exemple, si [DE] est un diamètre, alors 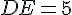cm.

Exercice 4 – calculer le périmètre d’un cercle.

a. Un cercle a pour rayon 12 cm. Quelle est la longueur d’un diamètre de ce cercle ?

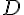
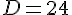
Le diamètre est égal à deux fois le rayon. Donc, . Par conséquent, cm.

b. Un cercle a pour diamètre 16,8 cm. Quelle est la longueur d’un rayon de ce cercle ?

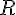
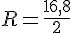
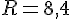
Le rayon est égal à la moitié du diamètre. Donc, . Par conséquent, cm.

Exercice 5 – tracer deux cercles.

1. Tracer le cercle de centre F et de rayon [FE] :

Pour ce faire, utilisez un compas. Placez la pointe du compas sur le point F et ouvrez-le jusqu’au point E. Tracez ensuite le cercle complet.

2. Tracer le cercle de diamètre [EG] :

Pour tracer un cercle de diamètre [EG], placez le milieu du segment [EG] comme centre du cercle. La longueur du rayon sera la moitié de la longueur du segment [EG], soit 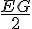. Utilisez un compas pour réaliser ce cercle.

Exercice 6 – reproduire une figure.

Pour reproduire la figure correctement, suivez ces étapes :

• Tracez un grand cercle avec un rayon couvrant les 9 unités de la grille.
• Positionnez deux cercles plus petits avec un rayon de 3 unités à chaque extrémité des axes horizontaux de la figure, de sorte qu’ils soient tangents à l’axe horizontal et se touchent entre eux.
• Utilisez un compas pour assurer la précision des demi-cercles qui complètent la forme yin-yang.
• Les centres des petits cercles doivent être placés sur la ligne médiane du grand cercle.

Exercice 7 – tracer cette figure.

Étapes pour tracer la figure :

1. Commencez par dessiner un carré 6×6 sur une feuille quadrillée.

2. Marquez le centre de chaque côté du carré, ainsi que les points médiaux des diagonales.

3. Tracez un cercle avec chaque centre aux points suivants :
– Centre de chaque côté du carré
– Centre global du carré
– Chaque point médian des diagonales

4. Notez que tous les cercles doivent avoir un rayon de 3 carreaux.

5. Vérifiez que les cercles se coupent au centre du carré, formant ainsi la figure géométrique de quatre lobes en pétales.

Exercice 8 – triangles particuliers.

Triangle isocèle : Fig. 7, Fig. 8

Triangle rectangle : Fig. 2, Fig. 4, Fig. 5

Triangle équilatéral : Fig. 6

Triangle quelconque : Fig. 1, Fig. 3, Fig. 9

Exercice 9 – coder l’angle droit d’un triangle.

Fig. 1 : Ce triangle est isocèle car il a deux côtés de même longueur. Il n’est pas rectangle car aucun angle n’est droit.

Fig. 2 : Ce triangle est équilatéral car il a trois côtés de même longueur. Aucun angle n’est droit.

Fig. 3 : Ce triangle est rectangle car un des angles est de 90° Il n’est ni isocèle ni équilatéral car les trois côtés sont de longueurs différentes.

Fig. 4 : Ce triangle est isocèle et rectangle car il a un angle droit et deux côtés de même longueur.

Exercice 10 – reproduire chaque triangle.

Figure 1 : Le triangle est un triangle équilatéral. Il suffit de copier exactement la même figure sur le quadrillage donné en respectant la taille et les proportions.

Figure 2 : Le triangle est un triangle isocèle. Assurez-vous que les côtés égaux sont bien reproduits avec la même longueur sur le quadrillage.

Figure 3 : Le triangle est un triangle scalène. Faites attention à la longueur de chaque côté et à leurs angles qui sont tous différents.

Figure 4 : Le triangle est un triangle isocèle. Vérifiez que les deux côtés égaux sont de même longueur et que l’angle entre eux est correct.