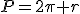Aires et périmètres : corrigé des exercices de maths en CM2 en PDF

Mis à jour le 22 avril 2026

Les aires et périmètres sont des notions essentielles en mathématiques que les élèves de CM2 doivent maîtriser. Comprendre ces concepts permet de développer des compétences cruciales telles que le calcul, la mesure et la résolution de problèmes. Dans cet article, nous allons corriger divers exercices sur ces thèmes, afin d’aider les élèves à renforcer leur compréhension et à améliorer leur confiance en mathématiques.

Exercice 1 – déterminer le périmètre de chaque figure.

Figure A :

La figure A est un carré de 4 unités de côté.

Le périmètre est donc : 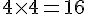$4\times4=16$

Figure B :

La figure B est un rectangle de 9 unités de longueur et 3 unités de largeur.

Le périmètre est : 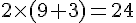$2\times(9+3)=24$

Figure C :

La figure C a une forme en « E » avec une longueur totale de bordure de 20 unités.

Le périmètre est :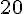

Figure D :

La figure D a une forme complexe de 24 unités de longueur totale de bordure.

Le périmètre est :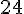

Exercice 2 – quel est le périmètre du carré ?.

Réponse a : Le périmètre d’un carré est donné par la formule $P=4\times c$ , où est la longueur du côté.

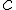
Pour un côté de 6 cm :

$P=4\times 6=24\text{ cm}$

Réponse b : Pour un côté de 4,6 cm :

$P=4\times 4,6=18,4\text{ cm}$

Exercice 3 – périmètre et carré.

Pour un carré de côté : le périmètre P = 4 x c .

a. c = 8 cm :

P = 4 x 8 = 32 cm

b. c = 1,5 cm

P = 4 x1,5 = 6 cm

c. P = 16 mm :

c = 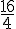$\frac{16}{4}$ = 4 mm

d. P = 22 m

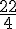
c = $\frac{22}{4}$ = 5,5 m

Exercice 4 – un rectangle de largeur l et de longueur L.

Réponse a :

La formule du périmètre est 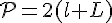$\mathcal{P}=2(l+L)$ .

Pour a : 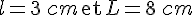$l=3\,cm\,\text{et}\,L=8\,cm$

Convertissons 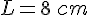$L=8\,cm$ en cm pour que les unités soient concordantes :

Périmètre : 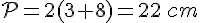$\mathcal{P}=2(3+8)=22\,cm$

Réponse b :

Pour b : 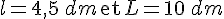$l=4,5\,dm\,\text{et}\,L=10\,dm$

Périmètre : 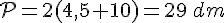$\mathcal{P}=2(4,5+10)=29\,dm$ .

Réponse c :

Pour c : 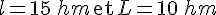$l=15\,hm\,\text{et}\,L=10\,hm$

Périmètre : 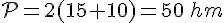$\mathcal{P}=2(15+10)=50\,hm$ (corrigé pour les valeurs de l).

Réponse d :

Pour d : 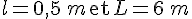$l=0,5\,m\,\text{et}\,L=6\,m$

Périmètre : 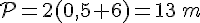$\mathcal{P}=2(0,5+6)=13\,m$ .

Exercice 5 – quel est la longueur du cercle ?.

La longueur de chaque figure correspond à un nombre entier d’unités de longueur (u.l.).

Chaque figure est composée de plusieurs arcs de cercle. Pour vérifier quel est l’intrus, calculons la longueur de chaque figure par rapport à l’unité de longueur donnée (le cercle de rayon 1 carreau, soit 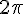$2\pi$ u.l.).

Fig. A : La figure est composée de 3 demi-cercles 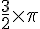$\frac{3}{2}\times\pi$ u.l.

Fig. B : La figure est composée de 2 cercles complets 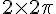$2\times2\pi$ u.l.

Fig. C : La figure est composée de 4 demi-cercles 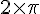$2\times\pi$ u.l.

Fig. D : La figure est composée de 4 demi-cercles identiques à celle de la Fig. C 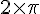$2\times\pi$ u.l.

Fig. E : La figure est composée de 2 cercles complets 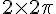$2\times2\pi$ u.l.

Intrus : La Fig. A est l’intrus car elle a une longueur de 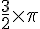$\frac{3}{2}\times\pi$ u.l., qui n’est pas un entier multiple de l’unité de longueur définie.

Exercice 6 – une fourmi et le tour d’un cercle.

La distance parcourue par la fourmi est le périmètre du cercle.

Le périmètre d’un cercle est donné par la formule :

$P=\pi\times d$

où d est le diamètre du cercle.

Dans cet exercice, le diamètre d est de 5 cm.

Donc,

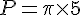
$P=\pi\times5$

En arrondissant le résultat à deux décimales, on obtient :

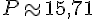
$P\approx15,71$

La fourmi parcourt donc environ 15,71 cm.

Exercice 7 – périmètre de différentes figures.

Réponse a :

Pour calculer le périmètre de chaque figure en unités de longueur (u.l.), nous allons additionner les demi-cercles qui composent chaque figure. Chaque demi-cercle correspond à une demi-unité de longueur.

Figure A :

La figure A est composée de 4 demi-cercles.

Périmètre de A : 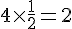$4\times\frac{1}{2}=2$ u.l.

Figure B :

La figure B est composée de 6 demi-cercles.

Périmètre de B : 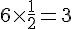$6\times\frac{1}{2}=3$ u.l.

Figure C :

La figure C est composée de 8 demi-cercles.

Périmètre de C : 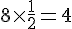$8\times\frac{1}{2}=4$ u.l.

Figure D :

La figure D est composée de 10 demi-cercles.

Périmètre de D : 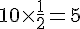$10\times\frac{1}{2}=5$ u.l.

Réponse b :

Convertissons les périmètres en centimètres, sachant que 1 u.l. ≈ 3,14 cm.

Figure A :

Périmètre de A : 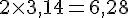$2\times3,14=6,28$ cm

Figure B :

Périmètre de B : 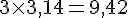$3\times3,14=9,42$ cm

Figure C :

Périmètre de C : 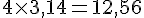$4\times3,14=12,56$ cm

Figure D :

Périmètre de D : 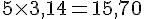$5\times3,14=15,70$ cm

Exercice 8 – calculer le périmètre de chaque figure.

Réponse pour la Fig. A :

Fig. A est un cercle complet. Pour calculer le périmètre d’un cercle, on utilise la formule :

$P=2\pi r$

Le rayon r est de 3 unités.

Donc, 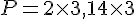$P=2\times3,14\times3$

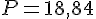
P=18,84

Réponse pour la Fig. B :

Fig. B est un demi-cercle. Pour calculer le périmètre d’un demi-cercle, on additionne la demi-circonférence et le diamètre :

$P=\pi r+d$

Le rayon r est de 3 unités. Le diamètre d est de 6 unités.

Donc, 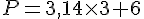$P=3,14\times3+6$

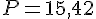
P=15,42

Réponse pour la Fig. C :

Fig. C est un quart de cercle. Pour calculer le périmètre d’un quart de cercle, on additionne un quart de circonférence et les deux rayons :

$P=\frac{\pi r}{2}+2r$

Le rayon r est de 3 unités.

Donc, 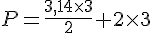$P=\frac{3,14\times3}{2}+2\times3$

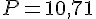
P=10,71

Exercice 9 – la lunule d’hippocrate.

Le demi-cercle en trait plein a un diamètre de 4 cm. Son périmètre est donc :

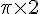
$\pi\times2$

Les deux demi-cercles en pointillés ont chacun un diamètre de 2 cm. Le périmètre combiné de ces deux demi-cercles est :

$2\times (\frac{\pi\times 2}{2}) = \pi\times 2$

Conclusion : Le périmètre du demi-cercle en trait plein est égal à celui des deux demi-cercles en pointillés.

Exercice 10 – exprimer l’aire de chaque figure.

Figure A : Cette figure est composée de 12 carrés unités complets.
Aire =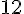

Figure B : Cette figure est composée de 10 carrés unités complets.
Aire =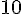

Figure C : Cette figure est composée de 11 carrés unités complets.
Aire =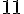

Figure D : Cette figure est composée de 9 carrés unités complets.
Aire =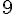

4.9/5 - (31512 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «aires et périmètres : corrigé des exercices de maths en CM2 en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 15 514 470 cours et exercices de maths téléchargés en PDF et 4 250 exercices.