Droites parallèles et perpendiculaires : corrigé des exercices de maths en CM2 en PDF
Mis à jour le 23 novembre 2025
Exercice 1 – droites perpendiculaires ?.
a. Non
b. Non
c. Non
d. Oui
e. Non
f. Oui
g. Oui
h. Non
Exercice 2 – repasser les droites perpendiculaires.
Les droites 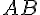
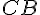
Exercice 3 – les droites sont-elles perpendiculaires ?.
a. (AB) et (IJ) : non
b. (HG) et (GJ) : oui
c. (BE) et (IJ) : oui
d. (DF) et (BG) : oui
e. (JE) et (AG) : non
f. (AB) et (HE) : non
Exercice 4 – tracer des droites perpendiculaires.
Figure a :
La droite (d1) est une droite verticale passant par le point A.
Figure b :
La droite (d1) est une droite horizontale passant par le point A.
Figure c :
La droite (d1) est une droite avec une pente opposée qui passe par le point A, formant un angle de 90° avec la droite (d).
Figure d :
La droite (d1) est une droite avec une pente opposée qui passe par le point A, formant un angle de 90° avec la droite (d).
Exercice 5 – construire des droites.
Pour construire les droites perpendiculaires à la droite (d) passant respectivement par les points A, B, C, D, E, F, G et H, suivez ces étapes :
- Identifiez chaque point A, B, C, D, E, F, G, H sur le plan.
- Utilisez un équerre pour mesurer un angle de 90° par rapport à la droite donnée (d).
- Tracez une droite à partir de chaque point en utilisant l’équerre pour assurer que la droite soit perpendiculaire à (d).
- Répétez cette étape pour chaque point.
Le processus assure que toutes les droites construites sont perpendiculaires à (d) et passent par leurs points respectifs.
Exercice 6 – compléter le tableau.
Droites perpendiculaires :
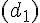
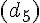
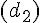
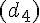
Droites parallèles :
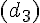
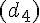
Exercice 7 – tracer en couleur des droites.
a.
Trace la droite (d1) en vert, perpendiculaire à la droite (d) et passant par le point B (c’est une verticale passant par B).
Trace la droite (d2) en rouge, parallèle à la droite (d) et passant par le point A (c’est une horizontale passant par A).
b.
Trace la droite (d1) en vert, perpendiculaire à la droite (d) et passant par le point B (la pente est l’inverse opposée de celle de (d)).
Trace la droite (d2) en rouge, parallèle à la droite (d) et passant par le point A (la pente est la même que celle de (d)).
c.
Trace la droite (d1) en vert, perpendiculaire à la droite (d) et passant par le point B (la pente est l’inverse opposée de celle de (d)).
Trace la droite (d2) en rouge, parallèle à la droite (d) et passant par le point A (la pente est la même que celle de (d)).
Exercice 8 – tracer la parallèle.
Pour résoudre cet exercice, il faut suivre les étapes suivantes :
- Tracer une droite parallèle à [RO]passant par le point C.
- Tracer une droite perpendiculaire à [RO] passant par le point R.
- L’intersection de ces deux droites se trouve au point K.
Le point K est donc situé à l’endroit où la parallèle à [RO] passant par C et la perpendiculaire à [RO] passant par R se rencontrent.
Exercice 9 – tracer des droites parallèles.
Pour compléter correctement cet exercice, nous devons suivre les étapes suivantes :
1. Trace la droite (NU).
2. Trace la droite parallèle à (NU) qui passe par le point F. Appelons cette droite (d).
3. Trace la droite perpendiculaire à (NU) qui passe par le point N. Cette droite coupe (NU) à un angle de 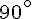
4. Les droites (d) et (e) sont sécantes en un point. Place ce point d’intersection K.
À ce stade, tu devrais voir un quadrilatère formé par les droites (NU), (d), et (e), avec l’intersection K.
Exercice 10 – utiliser le matériel de géométrie.
a. La droite parallèle à (AD) passant par C est la droite CG.
b. La droite parallèle à (AE) passant par D est la droite DG.
c. La droite perpendiculaire à (CE) passant par D n’existe pas dans cette configuration.
d. La droite perpendiculaire à (AB) passant par E est la droite EF.
Télécharger ou imprimer cette fiche «droites parallèles et perpendiculaires : corrigé des exercices de maths en CM2 en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.





