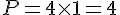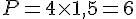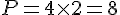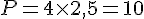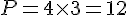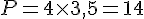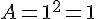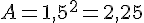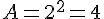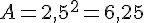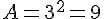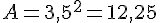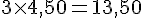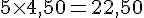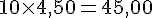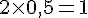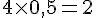Proportionnalité : corrigé des exercices de maths en CM2 en PDF

Mis à jour le 23 novembre 2025

La proportionnalité est un concept fondamental en mathématiques, particulièrement pour les élèves de CM2. Maîtriser cette compétence permet aux élèves de développer leur logique et d’améliorer leurs capacités en calcul et en raisonnement. Dans cet article, nous vous proposons des corrections d’exercices pour aider vos enfants à comprendre et appliquer les notions de proportionnalité, essentielles pour leur réussite scolaire.

Exercice 1 – problème des mini quiches.

a. Complétons le tableau :

	Pour 6	Pour 18	Pour 2	Pour 8
Farine (en g)	120	360	40	160
Jambon (en g)	150	450	50	200
Œuf	3	9	1	4
Lait (en cL)	60	180	20	80

b. Laurine ne dispose que de 10 œufs. Elle peut donc faire la recette pour :

Pour 6 personnes, il faut 3 œufs. Donc pour 10 œufs :

Nombre de personnes = 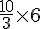$\frac{10}{3}\times 6$

Nombre maximal de personnes :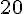

Exercice 2 – tarifs au cinéma.

a. Céline va 3 fois au cinéma ce mois-ci. Calcule le prix payé avec chaque tarif.

Tarif A : 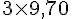$3\times 9,70$ = 29,10 €

Tarif B : 20,50 €

Tarif C : 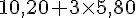$10,20+3\times 5,80$ = 27,60 €

b. Pour un mois, quel tarif est proportionnel au nombre de séances ?

Le tarif A est proportionnel au nombre de séances, car il dépend du nombre de séances

Exercice 3 – carré et proportionnalité.

a. Complète le tableau et justifie :

Pour calculer le périmètre d’un carré, on utilise la formule suivante :

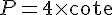
$P=4\times \text{cote}$

Complétons le tableau :

1 cm : $P=4\times 1=4$
1,5 cm : $P=4\times 1,5=6$
2 cm : $P=4\times 2=8$
2,5 cm : $P=4\times 2,5=10$
3 cm : $P=4\times 3=12$
3,5 cm : $P=4\times 3,5=14$

Le périmètre est proportionnel à la longueur du côté puisque le rapport entre le périmètre et le côté est constant (4).

b. Même question pour l’aire du carré :

Pour calculer l’aire d’un carré, on utilise la formule suivante :

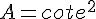
$A={cote}^2$

Complétons le tableau :

1 cm :
1,5 cm :
2 cm :
2,5 cm :
3 cm :
3,5 cm :

L’aire n’est pas proportionnelle à la longueur du côté car le rapport n’est pas constant.

Exercice 4 – compléter les tableaux de proportionnalité.

a. 1 gallon = 8 pintes

Pour 3 gallons : $3\times 8=24$
Pour 5 gallons : $5\times 8=40$
Pour 10 gallons : $10\times 8=80$

b. Un tour = 4,50 €

Pour 3 tours : $3\times 4,50=13,50$
Pour 5 tours : $5\times 4,50=22,50$
Pour 10 tours : $10\times 4,50=45,00$

c. 1 L = 0,5 kg

Pour 2 L : $2\times 0,5=1$
Pour 4 L : $4\times 0,5=2$
Pour 10 L : $10\times 0,5=5$

Exercice 5 – jeux et proportionnalité.

1. Prix de 13 jeux :

Le prix d’un jeu est 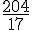$\frac{204}{17}$ €.

Donc, le prix de 13 jeux est :

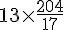
$13\times \frac{204}{17}$

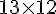
$13\times 12$ = 156 €.

2. Tapisser les fauteuils :

a. Temps pour 10 fauteuils :

Armel met 34 heures pour 4 fauteuils, donc pour 1 fauteuil, il met :

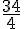
$\frac{34}{4}$

Donc pour 10 fauteuils, il met :

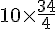
$10\times \frac{34}{4}$

heures.

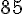
b. Nombre de fauteuils en 153 heures :

Armel peut tapisser 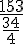$\frac{153}{\frac{34}{4}}$

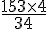
$\frac{153\times 4}{34}$ ≈ 18 fauteuils.

Exercice 6 – problème de la salle de bains.

a. Un sac de colle de 5 kg permet de poser 8 m² de carrelage. On cherche combien de colle est nécessaire pour 10 m².

Calcul :
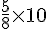
$\frac{5}{8}\times 10$

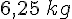
$6,25\,kg$

b. Un pot de 2,5 L de peinture couvre une surface de 30 m². On cherche combien de peinture est nécessaire pour 21 m².

Calcul :
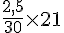
$\frac{2,5}{30}\times 21$

$1,75\,L$

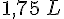
Exercice 7 – problème de consommation d’esence.

Réponse a :

Pour calculer la consommation d’essence de Martin aux 100 km :

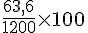
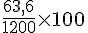
$\frac{63,6}{1200}\times 100$ = $\frac{63,6}{1200}\times 100$ = 5,3 L aux 100 km

Pour Amina :

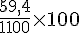
$\frac{59,4}{1100}\times 100$ = 5,4 L aux 100 km

Conclusion : La voiture d’Amina consomme le plus.

Réponse b :

Pour trouver la consommation d’Amina pour parcourir 1 200 km :

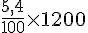
$\frac{5,4}{100}\times 1200$ = 64,8 L

Ce résultat confirme que la voiture d’Amina consomme plus que celle de Martin pour le même trajet.

Exercice 8 – conversions d’unités de longueur.

Pour convertir 26 miles en mètres :

Calcul :

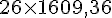
$26\times 1609,36$

Résultat :

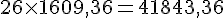
$26\times 1609,36=41843,36$

Donc, 26 miles correspondent à 41 843,36 mètres.

Pour convertir 385 yards en mètres :

Calcul :

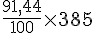
$\frac{91,44}{100}\times 385$

Résultat :

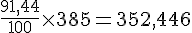
$\frac{91,44}{100}\times 385=352,446$

Donc, 385 yards correspondent à 352,446 mètres.

Exercice 9 – confitures et proportionnalité.

a. De quelle masse de sucre a-t-elle besoin si elle utilise 10,8 kg d’airelles ?

La masse de sucre nécessaire est proportionnelle à la masse d’airelles utilisée.

Relation de proportionnalité : 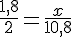$\frac{1,8}{2}=\frac{x}{10,8}$

Calculons x :

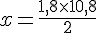
$x=\frac{1,8\times 10,8}{2}$

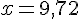
Elle a besoin de 9,72 kg de sucre.

b. De quelle masse d’airelles a-t-elle besoin si elle utilise 10,8 kg de sucre ?

Dans ce cas, la masse d’airelles est proportionnelle à la masse de sucre utilisée.

Relation de proportionnalité : 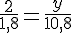$\frac{2}{1,8}=\frac{y}{10,8}$

Calculons y :

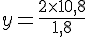
$y=\frac{2\times 10,8}{1,8}$

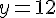
Elle a besoin de 12 kg d’airelles.

Exercice 10 – placement et proportionnalité.

a. Avec ce même taux, combien rapporte un placement de 12 700 € au bout d’un an ?

Le taux d’intérêt est calculé comme suit :

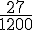
$\frac{27}{1200}$

Pour un placement de 12 700 €, cela donne :

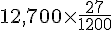
$12,700\times \frac{27}{1200}$

Le montant des intérêts est :

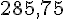
b. Quel est le montant initial d’un placement qui rapporte 427,50 € d’intérêts au bout d’un an ?

Utilisons le taux trouvé précédemment :

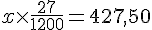
$x\times \frac{27}{1200}=427,50$

En résolvant pour :

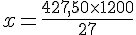
$x=\frac{427,50\times 1200}{27}$

Le montant initial est :

4.7/5 - (35861 votes)

Télécharger puis imprimer cette fiche en PDF.

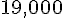
Télécharger ou imprimer cette fiche «proportionnalité : corrigé des exercices de maths en CM2 en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Droites parallèles et perpendiculaires

Les angles

Nombres entiers et calculs

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 331 585 cours et exercices de maths téléchargés en PDF et 4 250 exercices.