Médiatrice : corrigé des exercices de maths en 6ème en PDF
Mis à jour le 23 novembre 2025
Dans cet article, nous allons explorer la médiatrice, un concept clé en géométrie qui aide les élèves de sixième à développer des compétences fondamentales en maths. Comprendre la médiatrice permet non seulement de résoudre des problèmes géométriques, mais aussi d’améliorer des compétences telles que la logique et l’analyse. Les exercices que nous proposons aideront les élèves à maîtriser ce concept essentiel et à renforcer leur confiance en mathématiques.
Exercice 1 – jusitifier si un point est sur la médiatrice.
a. Figure : Le point P n’appartient pas à la médiatrice de [AB] car il n’est pas à égale distance des points A et B.
b. Figure : Le point P appartient à la médiatrice de [AB]. La médiatrice est la ligne perpendiculaire au segment [AB] passant par son milieu. Puisque P est sur la ligne perpendiculaire au milieu de [AB], il est équidistant de A et B.
c. Figure : Le point P n’appartient pas à la médiatrice de [AB] car les distances AP et BP ne sont pas égales.
d. Figure : Le point P n’appartient pas à la médiatrice de [AB] car les distances AP et BP ne sont pas égales.
Exercice 2 – médiatrice d’un quadrilatère.
a. Pour tracer la médiatrice du segment [AB], commence par déterminer le milieu de [AB]. Ensuite, trace une ligne perpendiculaire à [AB] passant par ce milieu. Répète le même processus pour le segment [BC].
b. Le point D est l’intersection des deux médiatrices, ce qui signifie qu’il est équidistant des points A, B, et C. En fait, le point D est le centre du cercle circonscrit au triangle ABC.
Exercice 3 – tracer la médiatrice d’un segment à la règle et au compas.
Réponse a :
Tracer le segment EF de longueur 6,1 cm, puis :
- Placez la pointe sèche du compas sur le point E, et tracez un arc au-dessus et un autre en dessous du segment.
- En gardant le même écartement, placez maintenant la pointe sèche du compas sur le point F, et tracez un autre arc qui croise les précédents.
- Reliez les deux points d’intersection des arcs. Cette ligne est la médiatrice du segment EF.
Réponse b :
Tracer le segment GH de longueur 7 cm, puis suivez les mêmes étapes que pour EF pour dessiner sa médiatrice.
Réponse c :
Tracer le segment IJ de longueur 8,3 cm, et appliquez le même processus pour construire sa médiatrice.
Réponse d :
Tracer le segment KL de longueur 5,2 cm, puis suivez les mêmes étapes pour obtenir sa médiatrice.
Réponse e :
Tracer le segment MN de longueur 4 cm, et procédez à la construction de sa médiatrice en suivant les mêmes instructions.
Réponse f :
Tracer le segment PR de longueur 8,7 cm, puis utilisez le même procédé pour construire la médiatrice.
Exercice 4 – exercice de justification.
Le raisonnement de Noam est partiellement correct mais nécessite une clarification. La droite 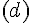
![[AB]](https://maths-pdf.fr/latex-images/5e32d4dbe98ef3af1b5123ccba43cbf7.png)
![[AB]](https://maths-pdf.fr/latex-images/5e32d4dbe98ef3af1b5123ccba43cbf7.png)
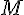
Pour montrer que 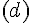
![[EC]](https://maths-pdf.fr/latex-images/8961d39164bd48d08fc513c38e3e0037.png)
![[EC]](https://maths-pdf.fr/latex-images/8961d39164bd48d08fc513c38e3e0037.png)

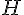
![[EC]](https://maths-pdf.fr/latex-images/8961d39164bd48d08fc513c38e3e0037.png)
Comme 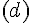
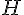
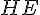
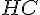
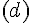
![[EC]](https://maths-pdf.fr/latex-images/8961d39164bd48d08fc513c38e3e0037.png)
Exercice 5 – médiatrice d’un segment et justification.
La droite (d) est la médiatrice du segment [AB] si elle vérifie deux conditions :
- Elle est perpendiculaire au segment [AB].
- Elle passe par le milieu du segment [AB].
Analyse des cas :
a) La droite (d) n’est pas perpendiculaire à [AB]. Non.
b) La droite (d) est perpendiculaire et passe par le milieu de [AB]. Oui.
c) La droite (d) est perpendiculaire mais ne passe pas par le milieu de [AB]. Non.
d) La droite (d) est perpendiculaire et passe par le milieu de [AB]. Oui.
e) La droite (d) n’est pas perpendiculaire à [AB]. Non.
En conclusion, la droite (d) est la médiatrice de [AB] dans les cas b) et d).
Exercice 6 – médiatrice et droite parallèles
1. Construction des points : Place trois points alignés A, B et C tels que AB = 5 cm et BC = 5,8 cm.
2. Construction des médiatrices :
– La médiatrice (d) de [AB] est la droite qui passe par le milieu de [AB] et est perpendiculaire à [AB].
– Le milieu de [AB] se trouve à 
– La médiatrice (d’) de [BC] est la droite qui passe par le milieu de [BC] et est perpendiculaire à [BC].
– Le milieu de [BC] se trouve à 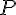
3. Démonstration que (d) et (d’) sont parallèles :
Les médiatrices (d) et (d’) sont par définition perpendiculaires à la droite (ABC), qui est une droite unique.
Deux droites perpendiculaires à une même droite sont parallèles entre elles.
Donc, (d) et (d’) sont parallèles.
Exercice 7 – médiatrice et calcul de longueur
1) Que représente la droite 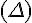
La droite 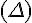
2) Trouver la longueur AN. Démontrer la réponse.
Étant donné que 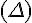
AM est donné comme étant 5 cm. Ainsi,
Exercice 8 – médiatrice et démonstration
1) Démontrer que les points B et D sont sur la médiatrice de [AC].
Pour démontrer que B et D sont sur la médiatrice de [AC], nous devons montrer qu’ils sont équidistants des points A et C.
Observons le triangle isocèle ABC :
Pour le point B :
On sait que 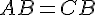
Pour le point D :
De même, 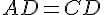
Comme B et D sont à égale distance de A et C, ils appartiennent tous deux à la médiatrice de [AC].
2) Que représente la droite (BD) pour le segment [AC] ?
La droite (BD) est la médiatrice du segment [AC]. Cela signifie qu’elle est perpendiculaire à [AC] et qu’elle passe par son milieu.
Par conséquent, tous les points de cette droite sont équidistants de A et C.
Exercice 9 – construction de médiatrices.
Le triangle ABC est isocèle.
Explication :
Lorsqu’on place un point C sur la médiatrice (d) du segment [AB], cela signifie que le point C est équidistant des points A et B.
Donc, les longueurs des segments [AC] et [BC] sont égales, d’où la nature isocèle du triangle ABC.
Exercice 10 – construction de triangle et médiatrice.
Étapes de construction :
1. Tracer le triangle : À l’aide d’une règle, tracez un triangle MNP.
2. Construction de la médiatrice de chaque côté :
a. Pour le côté MN :
– Placez la pointe du compas sur le point M et tracez un arc de cercle de rayon supérieur à la moitié de MN.
– Sans changer l’ouverture du compas, tracez un autre arc de cercle avec la pointe du compas sur le point N.
– Les deux arcs se croisent en deux points. Tracez une ligne droite entre ces deux points. Cette ligne est la médiatrice de MN.
b. Pour le côté NP :
– Répétez le même processus en plaçant d’abord la pointe du compas sur le point N puis sur le point P.
– Tracez la médiatrice de NP.
c. Pour le côté MP :
– Répétez le même processus en plaçant d’abord la pointe du compas sur le point M puis sur le point P.
– Tracez la médiatrice de MP.
Résultat : Les trois médiatrices se rencontrent en un point, appelé le centre du cercle circonscrit du triangle MNP.
Télécharger ou imprimer cette fiche «médiatrice : corrigé des exercices de maths en 6ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.






