Proportionnalité : corrigé des exercices de maths en 5ème en PDF

Mis à jour le 23 novembre 2025

La proportionnalité est une notion fondamentale en mathématiques, surtout pour les élèves de cinquième. Maîtriser ce concept permet aux élèves de développer des compétences essentielles telles que l’analyse, la comparaison et la résolution de problèmes. Dans cet article, nous vous proposons des corrections d’exercices pour aider les élèves à mieux comprendre et appliquer la proportionnalité dans divers contextes, renforçant ainsi leur confiance en mathématiques.

Exercice 1 – tableau de proportionnalité.

Exemple 1 :

Vérifions si chaque paire de valeurs a le même coefficient de proportionnalité.

Pour les valeurs 7 et 56 :

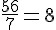
$\frac{56}{7}=8$

Pour les valeurs 11 et 88 :

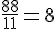
$\frac{88}{11}=8$

Pour les valeurs 13 et 104 :

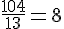
$\frac{104}{13}=8$

Pour les valeurs 21 et 168 :

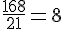
$\frac{168}{21}=8$

Pour les valeurs 25 et 200 :

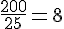
$\frac{200}{25}=8$

Conclusion : Le tableau est proportionnel avec un coefficient de proportionnalité de 8.

Exemple 2 :

Vérifions si chaque paire de valeurs a le même coefficient de proportionnalité.

Pour les valeurs 4 et 29,8 :

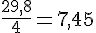
$\frac{29,8}{4}=7,45$

Pour les valeurs 7 et 52,15 :

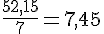
$\frac{52,15}{7}=7,45$

Pour les valeurs 8,4 et 62,58 :

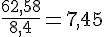
$\frac{62,58}{8,4}=7,45$

Pour les valeurs 12 et 89 :

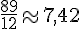
$\frac{89}{12}\approx7,42$

Pour les valeurs 100 et 745 :

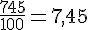
$\frac{745}{100}=7,45$

Conclusion : Le tableau n’est pas proportionnel car le coefficient entre 12 et 89 n’est pas exactement 7,45.

Exercice 2 – Compléter le tableau.

Calcul :

Pour trouver le coefficient de proportionnalité, choisissons les valeurs 3,2 et 2,4 :

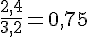
$\frac{2,4}{3,2}=0,75$

Appliquons ce coefficient aux autres valeurs :

Pour la case vide en haut :

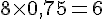
$8\times 0,75=6$

Pour la case vide en bas :

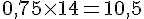
$0,75\times 14=10,5$

Conclusion : Le tableau complété est :

3,2	8	3	14
2,4	6	2,7	10,5

Exercice 2 – proportionnalité et vitesse.

Pour Françoise :

Longueur de la piste Le Flambeau : 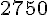m

Temps : 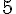minutes

Vitesse de Françoise : 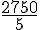$\frac{2750}{5}$ m/min

Donc, vitesse de Françoise : 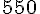m/min

Pour Georges :

Longueur de la piste Bois des Coqs : 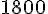m

Temps : 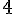minutes

Vitesse de Georges : 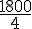$\frac{1800}{4}$ m/min

Donc, vitesse de Georges : 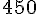m/min

Conclusion : Françoise a rejoint l’Arcelle en premier car elle a une vitesse plus élevée.

Exercice 3 – proportionnalité et calculs.

Analyse : Pour déterminer si cette situation traduit une proportionnalité, nous devons voir si les prix sont proportionnels aux nombres d’heures.

Calcul du prix par heure pour chaque option :

1 jour = 8 heures (de 9h à 17h) :

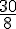
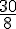
Prix par heure = $\frac{30}{8}$ = $\frac{30}{8}$ = 3,75€

1/2 journée (à partir de 12h) = 5 heures (de 12h à 17h) :

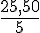
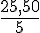
Prix par heure = $\frac{25,50}{5}$ = $\frac{25,50}{5}$ = 5,10€

1/2 journée a.M. (à partir de 13h) = 4 heures (de 13h à 17h) :

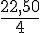
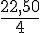
Prix par heure = $\frac{22,50}{4}$ = $\frac{22,50}{4}$ = 5,625€

Conclusion :

Les prix par heure sont différents pour chaque option. Donc, il n’y a pas de proportionnalité entre les heures et les prix. La situation ne traduit pas une situation de proportionnalité car le tarif par heure n’est pas constant.

Exercice 4 – calcul de la quatrième proportionnelle.

1. Tricot :

Il faut 14 mailles pour 8 cm de largeur. Pour 36 cm de largeur, le nombre de mailles nécessaires est calculé comme suit :

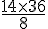
$\frac{14\times 36}{8}$

Calcul : 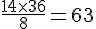$\frac{14\times 36}{8}=63$

2. Règle en acier :

Une règle de 20 cm³ a une masse de 148 grammes. Pour une règle de 35 cm³, la masse est calculée comme suit :

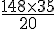
$\frac{148\times 35}{20}$

Calcul : 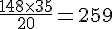$\frac{148\times 35}{20}=259$

Exercice 5 – tableau de proportionnalité.

1°) Compléter avec un coefficient de proportionnalité de 4.

Pour chaque valeur de la première ligne, nous devons la multiplier par 4 pour obtenir la valeur correspondante de la deuxième ligne.

3	12	0	15	…
6	4	0	3,75	7

2°) Dans chacun des trois tableaux suivants, peut-on trouver un opérateur multiplicatif comme dans les questions précédentes ?

Analysons chaque tableau :

Tableau 1 :

4	6	8
2	3	4

On peut vérifier qu’il existe un coefficient de proportionnalité en divisant chaque valeur de la première ligne par celle de la deuxième ligne : 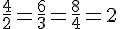${\frac{4}{2}=\frac{6}{3}=\frac{8}{4}=2}$

Tableau 2 :

12	13	14
3	4	5

Il n’existe pas de coefficient commun, car 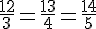${\frac{12}{3}=\frac{13}{4}=\frac{14}{5}}$

Tableau 3 :

2	3	4
6	9	12

Il existe un coefficient de proportionnalité, car 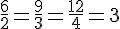${\frac{6}{2}=\frac{9}{3}=\frac{12}{4}=3}$

Exercice 7 – est-ce un tableau de proportionnalité.

Première ligne : Les ratios sont :

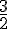
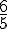
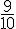
$\frac{3}{2}$ , $\frac{6}{5}$ , $\frac{9}{10}$ , etc.

Non proportionnels car les ratios ne sont pas tous égaux.

Deuxième ligne : Les ratios sont :

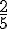
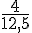
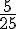
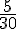
$\frac{2}{5}$ , $\frac{4}{12,5}$ , $\frac{5}{25}$ , $\frac{5}{30}$ , etc.

Non proportionnels car les ratios ne sont pas tous égaux.

Troisième ligne : Les ratios sont :

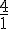
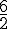
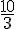
$\frac{4}{1}$ , $\frac{6}{2}$ , $\frac{10}{3}$ , etc.

Non proportionnels car les ratios ne sont pas tous égaux.

Quatrième ligne : Les ratios sont :

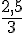
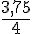
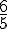
$\frac{2,5}{3}$ , $\frac{3,75}{4}$ , $\frac{6}{5}$ , etc.

Non proportionnels car les ratios ne sont pas tous égaux.

Exercice 8 – plan d’un couloir et échelle.

a. Exprimer ces deux dimensions en cm.

La longueur réelle du couloir est de 10 m. Pour exprimer cette mesure en centimètres, nous utilisons la conversion :

$10\ \text{m}=10\times 100\ \text{cm}=1000\ \text{cm}$

La longueur sur le plan est déjà donnée en centimètres : 20 cm.

b. Déterminer l’échelle de ce plan.

L’échelle est le rapport entre la longueur sur le plan et la longueur réelle. Elle est donnée par :

$\frac{\text{longueur\ sur\ le\ plan}}{\text{longueur\ réelle}}=\frac{20\ \text{cm}}{1000\ \text{cm}}$

Simpliﬁons ce rapport :

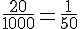
$\frac{20}{1000}=\frac{1}{50}$

L’échelle du plan est donc 1:50.

Exercice 9 – echelle d’un agrandissement.

On a agrandi un carré de 4 cm de côté en un carré de 6 cm de côté.

Pour trouver l’échelle d’agrandissement, on utilise la formule :

$\text{echelle}=\frac{\text{cote final}}{\text{cote initial}}$

Calcul :

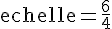
$\text{echelle}=\frac{6}{4}$

En simplifiant, on obtient :

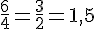
$\frac{6}{4}=\frac{3}{2}=1,5$

Donc, l’échelle utilisée est de 1,5.

Exercice 10 – maquette de bateau.

Pour calculer l’échelle de la maquette, il faut comparer la longueur de la maquette avec la longueur réelle du bateau.

La maquette mesure 21 cm, soit 0,21 m, et la longueur réelle est de 52,5 m.

L’échelle est donnée par le rapport : 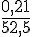$\frac{0,21}{52,5}$

Calculons ce rapport :

$\frac{0,21}{52,5} \approx \frac{1}{250}$

Ainsi, l’échelle de la maquette est 1:250.

4.8/5 - (36639 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «proportionnalité : corrigé des exercices de maths en 5ème en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Nombres relatifs

Angles

Calcul littéral

Priorités opératoires

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 363 560 cours et exercices de maths téléchargés en PDF et 4 250 exercices.