Limites et variations de suites : corrigé des exercices de maths en 1ère en PDF
Mis à jour le 25 novembre 2025
Dans cet article, nous allons explorer les limites et les variations de suites, des concepts essentiels pour les élèves de première en mathématiques. Comprendre ces notions vous permettra non seulement de maîtriser les suites numériques, mais aussi de développer des compétences analytiques cruciales lors de l’étude des fonctions. Grâce à des corrections d’exercices ciblés, nous vous aiderons à renforcer votre confiance et à exceller dans cette matière fondamentale.
Exercice 1 – fonction et monotonie d’une suite.
1) 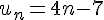
La fonction associée est 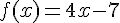
donc la suite 
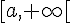
2) 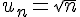
La fonction associée est 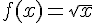
Cette fonction est croissante sur 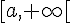

3) 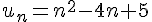
La fonction associée est 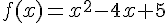
C’est une parabole qui admet un minimum au sommet. La dérivée 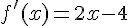
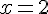
Ainsi, la suite est décroissante pour 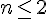
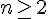
4) 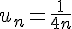
La fonction associée est 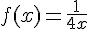
Cette fonction est décroissante sur 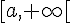

Exercice 2 – etudier la monotonie de suites.
1) Suite
Étudions les variations de la fonction 

Pour trouver le sens de variation, calculons la dérivée : 
La dérivée s’annule pour 
Donc, f est décroissante sur ![[a, \frac{13}{2}]](https://maths-pdf.fr/latex-images/6989ce94f78c89c668477ef150da5f7f.png)

Conclusion : La suite 


2) Suite
Étudions les variations de la fonction 

Calculons la dérivée :

Comme 

Conclusion :
La suite 
Exercice 3 – démontrer que la suite n’est pas monotone.
1) Pour la suite 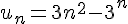
Considérons 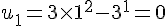
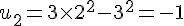
On a 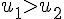
2) Pour la suite définie par 
Calculons quelques termes :
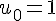
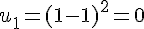
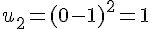
Ainsi, 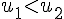
3) Pour la suite 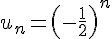
Considérons quelques termes :
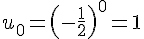
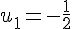
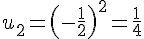
La suite oscille entre les valeurs positives et négatives, donc elle n’est pas monotone.
Exercice 4 – déterminer le sens de variation de la suite.
1) Suite 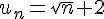
La fonction 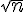
Donc, la suite 
2) Suite 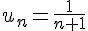
La fonction 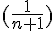
Donc, la suite 
3) Suite 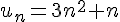
La fonction polynomiale 3n^2+n est croissante pour n \geq 0.
Donc, la suite 
4) Suite 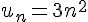
La fonction polynomiale 


5) Suite 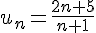
En étudiant le signe de la différence, on trouve que la suite 
6) Suite 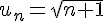
La fonction 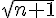

7) Suite 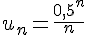
Cette suite décroît car le numérateur décroît plus vite que le dénominateur augmente.
Donc, la suite 
Exercice 5 – etudier la monotonie de ces suites en choisissant la méthode adaptée.
1) Suite : 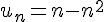
Cette suite est décroissante car pour tout 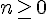
nous avons :
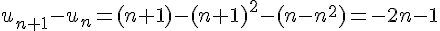
2) Suite : 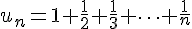
Cette suite est croissante car chaque terme ajouté est positif :
3) Suite : 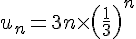
Cette suite est décroissante car 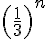
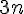
4) Suite : 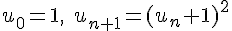
Cette suite est croissante car 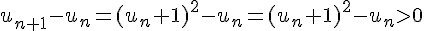
5) Suite : 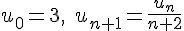
Cette suite est décroissante car chaque terme
6) Suite : 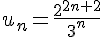
Cette suite est croissante car l’exposant de 2 croît plus vite que celui de 3 : 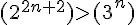
Exercice 6 – monotonie de différentes suites.
1) Suite 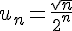
Pour étudier la monotonie, nous calculons 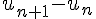
L’expression obtenue sera négative pour tous 
2) Suite 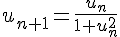
On vérifie par récurrence que la suite est décroissante.
Pour cela, montrons que 
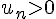
Cela est vrai car
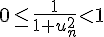
3) Suite 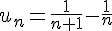
Cette suite est négative pour tout 
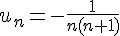
Suite Factorielle
La suite 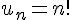
est plus grand que le précédent par le facteur 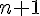
Exercice 7 – problème de plutonium et de suites.
1) Écrire 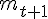
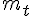
La quantité de plutonium 239 diminue de 0,003 % chaque année.
Ainsi, on peut écrire :
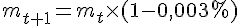
Ce qui donne :
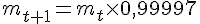
2) Étudier la nature de la suite (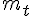
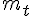
La suite (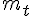
La formule générale d’une suite géométrique est :
Sachant que 
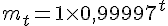
3) Étudier le sens de variations de la suite (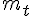
Puisque la raison q = 0,99997 est inférieure à 1, la suite (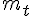
4) Déterminer, à l’aide d’un tableur, le nombre d’années nécessaires pour diminuer de moitié la masse de plutonium 239 dans ce déchet.
Il s’agit de résoudre l’équation suivante :
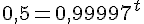
En prenant le logarithme de chaque côté, nous obtenons :
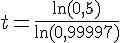
Calculons cette valeur avec un tableur pour déterminer la demi-vie :
Ainsi, on trouve environ 
Cette durée s’appelle demi-vie radioactive du plutonium 239.
Exercice 8 – suite arithmétique et monotonie.
Réponse 1 :
Pour la suite arithmétique de premier terme 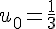
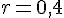

La raison 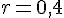

Réponse 2 :
Pour la suite arithmétique de premier terme 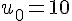
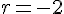

La raison 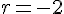

Réponse 3 :
Pour la suite arithmétique de premier terme 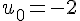
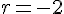

La raison 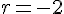

Réponse 4 :
Pour la suite arithmétique de premier terme 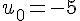
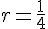

La raison 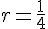

Exercice 9 – suite géométrique et monotonie.
1. Suite 1 :
Suite géométrique de premier terme 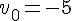
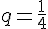
- Le terme suivant est strictement inférieur au terme précédent car
- Cette suite est décroissante.
2. Suite 2 :
Suite géométrique de premier terme 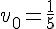
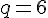
- Le terme suivant est strictement supérieur au terme précédent car
- Cette suite est croissante.
3. Suite 3 :
Suite géométrique de premier terme 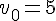
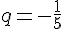
- La suite oscille entre des valeurs positives et négatives puisque
- Cette suite est non monotone.
4. Suite 4 :
Suite géométrique de premier terme 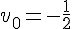
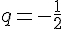
- La valeur absolue des termes diminue mais les signes alternent, donc
- Cette suite est non monotone.
Exercice 10 – par lecture graphique, indiquer si la suite est monotone.
Réponse pour la suite 1 :
La suite n’est pas monotone. Elle oscille autour de la valeur 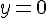
Réponse pour la suite 2 :
La suite est constante et monotone. La limite semble être 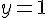
Télécharger ou imprimer cette fiche «limites et variations de suites : corrigé des exercices de maths en 1ère en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.














