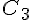Dérivée : corrigé des exercices de maths en 1ère en PDF
Mis à jour le 25 novembre 2025
Exercice 1 – donner le tableau de signes.
Pour établir le tableau de signes de f'(x), observons les variations de la courbe de f(x) :
1. Intervalle ![]-\infty; 0]](https://maths-pdf.fr/latex-images/449d0697da290a3f12374963fd0ec461.png)
La fonction est croissante car la courbe monte, donc 
2. Intervalle ![[0; 0,5]](https://maths-pdf.fr/latex-images/e9e5e20ae151f8e0a7faa8df6faefc43.png)
La fonction continue de monter, donc 
3. Point 
On atteint un maximum, donc 
4. Intervalle ![[ 0,5; 1]](https://maths-pdf.fr/latex-images/13aa56d5ae292d4c782d09d5824fd2fe.png)
La fonction descend, donc 
5. Point x = 1 :
La dérivée n’est pas définie f n’est pas dérivable).
6. Intervalle ![]1;+\infty]](https://maths-pdf.fr/latex-images/aad3e599988219a258ff776bb5a920e6.png)
La fonction descend puis remonte; ainsi, sans croisement de l’axe des abscisses entre les deux mouvements, la dérivée reste 
Tableau de signes de f ‘(x) :
| x | -∞ | 0 |  \ \ |
1 | +∞ |
| f ‘(x) | + | + | 0 | / | … |
Exercice 2 – parmi ces fonctions quelle est celle de la dérivée de f ?.
Pour déterminer laquelle des fonctions 
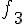
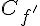
La courbe 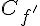
Cela signifie que la fonction d’origine est décroissante puis croissante au minimum de la dérivée.
En observant les graphiques des fonctions :
-
-
-
Conclusion : La fonction f_2 est celle qui a pour dérivée la fonction représentée par 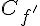
Exercice 3 – volume maximal d’un cône inclus dans une sphère.
Pour déterminer le volume maximal du cône, on choisit d’abord la variable r = HA.
Le volume V d’un cône est donné par la formule :
Dans notre cas :
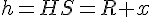
La relation dans le triangle rectangle OHA donne :
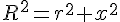
d’où :
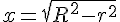
Substituons x dans l’expression de h :
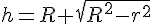
Le volume du cône s’exprime alors en fonction de r :
Pour maximiser V(r), on dérive par rapport à r et on résout V'(r) = 0.
De la même manière, en choisissant la variable x = HO, on a :
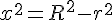
et en substituant dans l’expression du volume, nous suivons un processus similaire.
Dans les deux cas, une optimisation standard en utilisant le calcul différentiel montrera que le volume maximal est atteint pour :
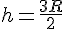
Cela donne un volume maximal :
Exercice 4 – une boîte de conserve et la surface de métal.
1) Calcul de la surface :
La surface totale d’une boîte cylindrique est la somme de la surface latérale et des deux bases :
Surface latérale :
Surface des deux bases :
Le volume 
En substituant, on obtient :
Ce qui simplifie à :
2) Étude de la fonction S :
La fonction 
0″>
Étudions sa dérivée pour trouver les minimums :
Pour annuler la dérivée :
![r=\sqrt[3]{\frac{\mathcal{V}}{2\pi}}](https://maths-pdf.fr/latex-images/076d2d68ec26f3060820b33e65869480.png)
3) Dimensions optimales :
En utilisant la valeur de 
Finalement, ces valeurs minimisent la surface de métal utilisée.
4) Application numérique :
Pour un volume donné, par exemple 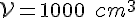
Calculons ![r=\sqrt[3]{\frac{1000}{2\pi}}](https://maths-pdf.fr/latex-images/2559adbff2fd4da073363a8f7f37203b.png)
Puis, calculons
Cela donne les dimensions optimales de la boîte.
Exercice 5 – courbe de f et de f’.
Pour déterminer quelle courbe représente f et quelle représente sa dérivée f ‘ , observons les variations des fonctions et le signe de la dérivée.
La courbe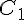
De plus, elle croise l’axe des abscisses, ce qui correspond aux valeurs des x où f ‘ est zéro.
La courbe C_2 présente une forme continue sans changement de signe radical, plus caractéristique d’une fonction 
Ainsi, la courbe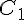

Exercice 6 – tableau de signes d’une fonction.
Réponse 1 :
Pour le premier exercice, la fonction 
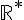
1. ![]-\infty < x< 0 ]](https://maths-pdf.fr/latex-images/5f020a1670b6a4101bf9d3f37fdf0c11.png)
Donc 
2. 

Il y a un extremum.
3. 

Donc 
4. 

Il y a un extremum.
5. ![[0 < x < 1]](https://maths-pdf.fr/latex-images/ddbfbd3ba0eeba04171ac81cb818f919.png)

Donc 
6. 

7. 

Donc 
Comme 

Réponse 2 :
Pour le second exercice, la fonction 
![]0 ; +\infty[](https://maths-pdf.fr/latex-images/7c82b1a398e0e78d779a5cbfa6e7bf51.png)
1. 

Donc 
2. 

3. 
Donc 
4. 

Il y a un extremum.
5.
Donc 
6. 

Il y a un extremum.
7. 

Donc 
Comme 

Exercice 7 – ensemble de définition et position relative par rapport à la tangente.
a) Fonction : 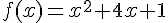
1) Ensemble de définition et de dérivabilité :
La fonction est définie et dérivable sur 
2) Équation de la tangente 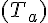
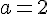
Dérivée : 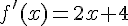
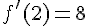
Équation : 
3) Positions relatives : Étudier la différence entre 
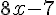
b) Fonction : 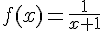
1) Ensemble de définition et de dérivabilité :
Définie et dérivable sur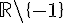
2) Équation de la tangente 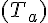
Dérivée : 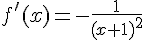
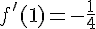
Équation : 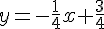
3) Positions relatives :
Étudier la différence entre 
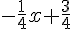
c) Fonction : 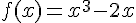
1) Ensemble de définition et de dérivabilité :
La fonction est définie et dérivable sur 
2) Équation de la tangente 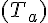
Dérivée : 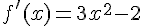
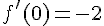
Équation : 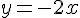
3) Positions relatives : Étudier la différence entre 
d) Fonction : 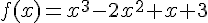
1) Ensemble de définition et de dérivabilité : La fonction est définie et dérivable sur 
2) Équation de la tangente 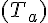
Dérivée : 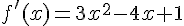
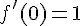
Équation : 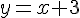
3) Positions relatives : Étudier la différence entre
e) Fonction : 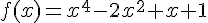
1) Ensemble de définition et de dérivabilité :
La fonction est définie et dérivable sur 
2) Équation de la tangente 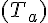
Dérivée : 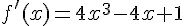
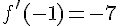
Équation : 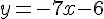
3) Positions relatives :
Étudier la différence entre 
f) Fonction : 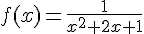
1) Ensemble de définition et de dérivabilité : Définie et dérivable sur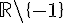
2) Équation de la tangente 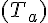
Dérivée : 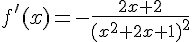
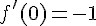
Équation : 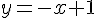
3) Positions relatives : Étudier la différence entre 
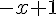
g) Fonction : 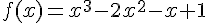
1) Ensemble de définition et de dérivabilité :
La fonction est définie et dérivable sur 
2) Équation de la tangente 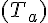
Dérivée : 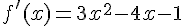
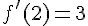
Équation : 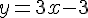
3) Positions relatives :
Factoriser l’expression 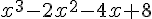
Exercice 8 – fonction dérivable à droite de 0.
Pour déterminer la dérivabilité de la fonction 
Étude de la dérivabilité à droite (pour 
Pour

Sa dérivée est donc 
En 
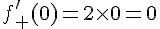
Conclusion :
La fonction est dérivable à droite en 0, avec 
Étude de la dérivabilité à gauche (pour 
Pour 

Sa dérivée est donc 
En 
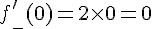
Conclusion :
La dérivée à gauche en 0, est aussi égale à 0.
Cependant, à l’analyse des limites de 

Cependant, cette information ne tient pas sa dérivabilité à gauche stricte.
Conclusion générale :
La fonction est dérivable à droite en 
montre qu’une bonne compréhension vient d’identifier la transition en les deux termes séparés en chaque côté de 0.
Exercice 9 – fonction dérivable et problème.
1) Les points M et N sont symétriques par rapport à l’axe des ordonnées car pour une fonction paire, 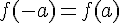
2) La dérivée de f en -a est l’opposé de la dérivée en a :
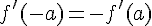
3) Pour a = 0, on a 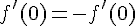
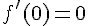
4) Pour une fonction impaire, les points M et N sont symétriques par rapport à l’origine car 
5) La dérivée de f satisfait :
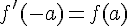
Exercice 10 – signe de f’ et sens de variation.
1. Première fonction :
Soit 
Les racines de 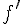

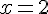
Tableau de signes de 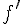
| x | -∞ | 1 | 2 | +∞ |
| 
Conclusion :
La fonction 
![]-\infty, 1]](https://maths-pdf.fr/latex-images/c4075ba3edf6a4ece53ddbea98b3c9aa.png)
![[1, 2]](https://maths-pdf.fr/latex-images/04cd0e0151f352e7fd414d694a604136.png)

2. Deuxième fonction :
Avec 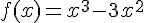
Calcul de la dérivée : 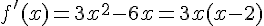
Les racines de 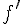
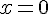
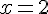
Tableau de signes de 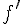
| x | -∞ | 0 | 2 | +∞ |
| 
Conclusion :
La fonction 
![]-\infty, 0]](https://maths-pdf.fr/latex-images/c31737d615ac8e7a597a175ab99191c9.png)
![[0, 2]](https://maths-pdf.fr/latex-images/6635d8e8b50fce682f2f7a19308db4ad.png)

3. Tableau de variations donné :
Nous pouvons observer que la fonction descend puis monte :
– Sur ![]-\infty, 3[](https://maths-pdf.fr/latex-images/1e21740764274049a94455ab40e93644.png)

– Sur ![[3, 4]](https://maths-pdf.fr/latex-images/d8b28cb48c33f4af8c04df2c49a58b88.png)

– Sur 

Conclusion :
Le signe de 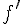
Télécharger ou imprimer cette fiche «dérivée : corrigé des exercices de maths en 1ère en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.