Probabilités et variables aléatoires : corrigé des exercices de maths en 1ère en PDF

Mis à jour le 25 novembre 2025

Dans cet article, nous allons aborder les probabilités et les variables aléatoires, des notions cruciales pour les élèves de 1ère.

La maîtrise de ces notions permet de développer des compétences essentielles en statistiques et en analyse de données, qui sont indispensables pour réussir dans les matières scientifiques.

En comprenant les probabilités, les élèves de première peuvent mieux appréhender les incertitudes et prendre des décisions éclairées au quotidien.

Exercice 1 – déterminer des événements contraires.

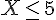
1) Événement contraire de X > 5 : $X\leq5$

2) Événement contraire de « X est supérieur ou égal à 2 » : 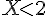X<2

3) Événement contraire de $(X \leq\, 3)$ : X>3

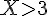
4) Événement contraire de « X est inférieur ou égal à 4 » : 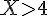X>4

Exercice 2 – donner l’affirmation contraire.

1) Il y a au moins un élève de la classe qui ne sera pas admis au bac.

2) Paul ne mange pas tous les jours à la cantine.

3) Je vais parfois au cinéma le dimanche.

4) Il y a au moins un élève de la classe qui ne possède pas de téléphone portable.

Exercice 3 – loi de probabilité.

Pour que la table définisse une loi de probabilité, la somme des probabilités doit être égale à 1.

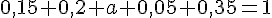
Calculons la somme des autres probabilités :

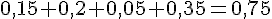
On a donc :

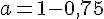
Donc, 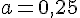a=0,25

Exercice 4 – calculer des probabilités.

1. Quelles sont les probabilités données :

Les probabilités données dans l’arbre sont :

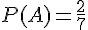
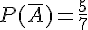
– $P(A)=\frac{2}{7}$ et $P(\overline{A})=\frac{5}{7}$

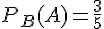
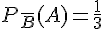
– $P_{B}(A)=\frac{3}{5}$ et $P_{\overline{B}}(A)=\frac{1}{3}$

2. Déterminer les probabilités manquantes :

Les probabilités complémentaires manquantes sont :

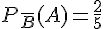
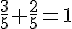
– $P_{\overline{B}}(A)=\frac{2}{5}$ (car $\frac{3}{5}+\frac{2}{5}=1$ )

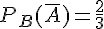
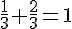
– $P_{B}(\overline{A})=\frac{2}{3}$ (car $\frac{1}{3}+\frac{2}{3}=1$ )

3. En déduire 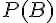P(B) :

Pour calculer 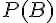P(B) , on utilise la formule de la probabilité totale :

$P(B)=P(B|A)\times \, P(A)+P(B|\overline{A})\times \, P(\overline{A})$

Donc :

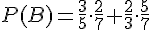
$P(B)=\frac{3}{5}\cdot\frac{2}{7}+\frac{2}{3}\cdot\frac{5}{7}$

Calculons chaque terme :

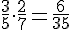
$\frac{3}{5}\cdot\frac{2}{7}=\frac{6}{35}$

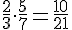
$\frac{2}{3}\cdot\frac{5}{7}=\frac{10}{21}$

Pour additionner, mettons au même dénominateur :

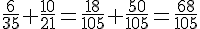
$\frac{6}{35}+\frac{10}{21}=\frac{18}{105}+\frac{50}{105}=\frac{68}{105}$

Donc, 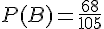$P(B)=\frac{68}{105}$

Exercice 5 – calculer la probabilité de AUB.

1. Calcul de P(A ∪ B) :

La probabilité de l’union de deux événements est donnée par la formule :

$P(A\cup B) = P(A) + P(B) - P(A\cap B)$

En remplaçant par les valeurs données :

$P(A\cup B) = 0,3 + 0,6 - 0,2 = 0,7$

2. Calcul de P_B(A) :

Il s’agit de la probabilité de A sachant B :

$P_B(A) = \frac{P(A\cap B)}{P(B)}$

En remplaçant par les valeurs données :

$P_B(A) = \frac{0,2}{0,6} = \frac{1}{3}$

3. Calcul de P_A(B) :

Il s’agit de la probabilité de B sachant A :

$P_A(B) = \frac{P(A\cap B)}{P(A)}$

En remplaçant par les valeurs données :

$P_A(B) = \frac{0,2}{0,3} = \frac{2}{3}$

Exercice 6 – des événements indépendants ?.

Pour déterminer si A et B sont indépendants, nous devons vérifier si :

$\text{P}(A\cap B)=\text{P}(A)\times \text{P}(B)$

Calculons le produit des probabilités de A et B :

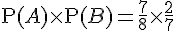
$\text{P}(A)\times\text{P}(B)=\frac{7}{8}\times\frac{2}{7}$

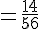
$=\frac{14}{56}$

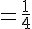
$=\frac{1}{4}$

Comparons avec P(A ∩ B) :

$\text{P}(A\cap B)=\frac{1}{4}$

Conclusion :

Les événements A et B sont indépendants car le produit des probabilités est égal à la probabilité de l’intersection.

Exercice 7 – calculer deux probabilités.

1. Correction du tableau :

	A_1	$\overline{A_1}$	Total
A_2	0,55	0,15	0,7
$\overline{A_2}$	0,25	0,05	0,3
Total	0,8	0,2	1

2. Calcul des probabilités :

Pour calculer 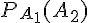$P_{A_1}(A_2)$ , on utilise la formule :

$P_{A_1}(A_2)=\frac{P(A_1\cap A_2)}{P(A_1)}$

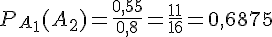
$P_{A_1}(A_2)=\frac{0,55}{0,8}=\frac{11}{16}=0,6875$

Pour calculer 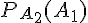$P_{A_2}(A_1)$ , on utilise la formule :

$P_{A_2}(A_1)=\frac{P(A_2\cap A_1)}{P(A_2)}$

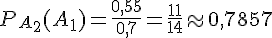
$P_{A_2}(A_1)=\frac{0,55}{0,7}=\frac{11}{14}\approx0,7857$

Exercice 8 – calculer la probabilité conditionnelle.

Solution 1 :

Calculer $P(A\cap B)$ .

Nous savons que :

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$ .

En remplaçant par les valeurs connues :

$0,9=0,45+0,6-P(A\cap B)$ .

En résolvant pour $P(A\cap B)$ :

$P(A\cap B)=0,45+0,6-0,9=0,15$ .

Solution 2 :

En déduire 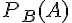P_B(A) et P_A(B) .

$P_B(A)=\frac{P(A\cap B)}{P(B)}=\frac{0,15}{0,6}=0,25$ .

$P_A(B)=\frac{P(A\cap B)}{P(A)}=\frac{0,15}{0,45}=\frac{1}{3}\approx0,33$ .

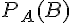
Exercice 9 – un arbre de probabilités.

1. Recopier et compléter l’arbre.

$P(A\cap B)=0,7\times 0,2=0,14$

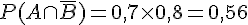
$P(A\cap\overline{B})=0,7\times0,8=0,56$

$P(\overline{A}\cap B)=0,3\times 0,6=0,18$

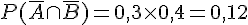
$P(\overline{A}\cap\overline{B})=0,3\times0,4=0,12$

2. Calculer 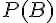P(B) .

$P(B)=P(A\cap B)+P(\overline{A}\cap B)=0,14+0,18=0,32$

Exercice 10 – probabilités indépendantes.

1. Calculer $P(A \cap B)$ :

Les événements A et B sont indépendants. Donc :

$\mathbb{P}(A \cap B) = \mathbb{P}(A) \times \mathbb{P}(B)$

En remplaçant par les valeurs données :

$\mathbb{P}(A \cap B) = 0,5 \times 0,7 = 0,35$

2. Calculer $P(\overline{A} \cap B)$ de deux manières différentes :

Méthode 1 :

Nous savons que :

$\mathbb{P}(\overline{A} \cap B) = \mathbb{P}(B) - \mathbb{P}(A \cap B)$

En remplaçant par les valeurs :

$\mathbb{P}(\overline{A} \cap B) = 0,7 - 0,35 = 0,35$

Méthode 2 :

En utilisant l’indépendance et la complémentarité :

$\mathbb{P}(\overline{A} \cap B) = \mathbb{P}(\overline{A}) \times \mathbb{P}(B)$

Or, $P(\overline{A}) = 1 - P(A) = 0,5$

Donc :

$\mathbb{P}(\overline{A} \cap B) = 0,5 \times 0,7 = 0,35$

4.9/5 - (35485 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «probabilités et variables aléatoires : corrigé des exercices de maths en 1ère en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Statistiques

Fonctions usuelles

Les suites

Angles orientés et trigonométrie

Second degré et polynômes

Limites et variations de suites

Produit scalaire dans le plan

Vecteurs et droites du plan

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 753 693 cours et exercices de maths téléchargés en PDF et 4 250 exercices.