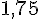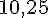Statistiques : corrigé des exercices de maths en 1ère en PDF

Exercice 1 – simplifier des sommes.

Réponse 1 :

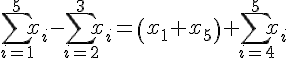
Réponse 2 :

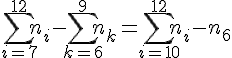
Exercice 2 – diagramme en boîte et intervalle interquartile.

1) Lire le minimum, Q1, la médiane, Q3 et le maximum de cette série statistique.

Minimum :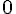

Q1 :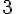

Médiane :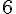

Q3 :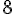

Maximum :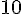

2) En déduire l’intervalle interquartile.

L’intervalle interquartile est calculé comme :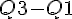

Intervalle interquartile :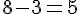

Exercice 3 – compléter le diagramme en boîte.

L’étendue est la différence entre la valeur maximale et la valeur minimale. Ici, elle doit être de 11. Supposons que la valeur minimale soit 7, alors la valeur maximale sera .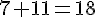

La médiane, qui est la valeur centrale, doit être 12.

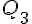
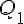
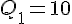
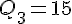
L’écart interquartile (différence entre le troisième quartile et le premier quartile ) doit être 5. Si nous posons , alors .

En résumé:

• Valeur minimale : 7
• Premier quartile : 10
• Médiane : 12
• Troisième quartile : 15
• Valeur maximale : 18

Exercice 4 – déterminer les quartiles et diagramme en boîte.

1) Détermination des quartiles et de la médiane :

Pour déterminer les quartiles et la médiane, nous devons d’abord organiser l’ensemble des données en une liste ordonnée. La liste ordonnée du nombre d’articles est :

2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 6, 8, 8, 8, 8, 8, 8, 8, 8, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 8, 8, 8, 8, 8, 8, 8, 8, 1, 1, 1, 1.

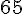
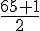
Le nombre total de clients est . Pour déterminer la médiane, nous prenons le milieu de cette liste ordonnée. La médiane est le -ème terme, soit le 33ème terme. Donc, la médiane est :

Médiane = 5

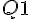
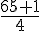
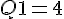
Pour le premier quartile , nous prenons la valeur au -ème terme, soit le 16ème terme :

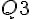
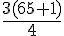
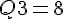
Pour le troisième quartile , nous prenons la valeur au -ème terme, soit le 49ème terme :

2) Diagramme en boîte :

Le diagramme en boîte est constitué des éléments suivants :

• Le minimum = 2
• 
• Médiane = 5
• 
• Le maximum = 10

Le diagramme en boîte résume ainsi la répartition des données.

Exercice 5 – déterminer la médiane et jeux vidéos.

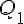
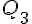
1) Déterminer \(Q_1\), \(Q_3\) et la médiane de cette série.

La série triée est : 0 ; 1 ; 2 ; 3 ; 5 ; 6 ; 7 ; 10 ; 11 ; 12.

Pour un ensemble de 10 valeurs :

• Médiane :
• Premier quartile \(Q_1\) : Position \(\frac{10+1}{4}=2,75\), donc \(Q_1\) est entre 1 et 2, soit
• Troisième quartile \(Q_3\) : Position \(\frac{3\times (10+1)}{4}=8,25\), donc \(Q_3\) est entre 10 et 11, soit

2) Tracer le diagramme en boîte de cette série.

Le diagramme en boîte se base sur les valeurs suivantes : min = 0, \(Q_1 = 1,75\), médiane = 5,5, \(Q_3 = 10,25\), max = 12. (Diagramme non dessiné ici)

3) De quel phénomène important le diagramme en boîte ne rend-il pas compte ?

Le diagramme ne montre pas l’ordre chronologique des valeurs ni la tendance au fil du temps.

4) Proposer une représentation graphique rendant compte de ce phénomène.

Une courbe chronologique, telle qu’un graphique en ligne, pourrait mieux illustrer l’évolution du nombre de jeux achetés par an.

Exercice 6 – tracer les diagrammes en boîtes des séries.

1) Déterminer le nombre d’élèves de chaque classe.

Pour la classe 1^re S1 :

Effectifs : 5 + 4 + 0 + 3 + 5 + 6 + 4 + 5 + 6 + 6 =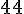

Pour la classe 1^re S2 :

Effectifs : 4 + 5 + 4 + 2 + 3 + 6 + 7 + 4 + 5 + 1 =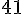

2) Tracer les diagrammes en boîtes des deux séries sur le même graphique.

Pour tracer les diagrammes en boîtes, identifions les valeurs importantes :

– Médiane pour S1 : notes 5 et 6, donc médiane =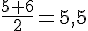

– Médiane pour S2 : note 5

– Premier quartile pour S1 : entre 3 et 4

– Premier quartile pour S2 : 4

– Troisième quartile pour S1 : 8

– Troisième quartile pour S2 : 8

Tracer maintenant les boîtiers et les moustaches avec ces valeurs.

3) Comparer les deux classes.

Comparons leurs médianes et leurs étendues interquartiles :

– La médiane de la S1 est légèrement plus élevée que celle de la S2, indiquant une meilleure performance globale.

– L’étendue interquartile est similaire, ce qui montre une dispersion semblable des notes autour de la médiane.

– Les deux classes ont des valeurs extrêmes proches, mais S1 a des élèves avec des notes plus élevées (9 et 10).

Exercice 7 – une étude de séries statistiques.

1) La série la plus homogène est celle avec le plus petit écart interquartile (e).

2) Démonstration :

Soit 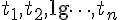les valeurs des tailles en mètres.

Lorsque les tailles sont exprimées en centimètres, chaque valeur est multipliée par 100 : .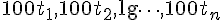

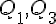
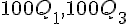
Si sont les premiers et troisièmes quartiles de la série en mètres, les quartiles de la série en centimètres deviennent : .

L’écart interquartile est donc multiplié par 100 : .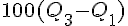

3) Discussion sur l’homogénéité :

On ne peut pas simplement comparer les écarts interquartiles (e et 100e) pour évaluer l’homogénéité sans prendre en compte l’échelle des séries. D’autres mesures comme le coefficient de variation peuvent être envisagées pour plus de pertinence.

Exercice 8 – salaires nets mensuels des femmes et hommes en France.

Pour les femmes :

Médiane : environ 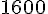euros

Écart interquartile : environ 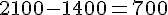euros

Pour les hommes :

Médiane : environ 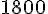euros

Écart interquartile : environ 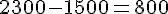euros

Exercice 9 – algorithme et quartiles.

Réponse 1 :

Cet algorithme demande à l’utilisateur de saisir des valeurs jusqu’à ce que le compteur i atteigne 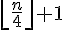, où n est le nombre de valeurs demandé initialement. Ensuite, il affiche la dernière valeur saisie et un message. Actuellement, l’algorithme ne trie pas les valeurs, donc le message sur l’ordre est inapproprié.

Amélioration : Pour être plus pertinent, il faudrait enregistrer toutes les valeurs saisies dans une liste, les trier, et ne pas afficher la dernière valeur saisie comme le script actuel mais plutôt un message pertinent après vérification de l’ordre.

Réponse 2 :

Pour modifier l’algorithme afin qu’il affiche le troisième quartile, il faut :

1. Créer une liste pour stocker les valeurs saisies.

2. Trier la liste après saisie de toutes les valeurs.

3. Calculer l’indice du troisième quartile comme :

4. Afficher la valeur correspondante au troisième quartile dans la liste triée.

Exercice 10 – algorithme et série statistiques.

Pour que l’algorithme vérifie à chaque étape si la série est bien ordonnée, nous complétons les pointillés de la manière suivante :

9. Si 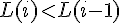<img class="LatexImg" src="https://maths-pdf.fr/cgi-bin/mimetex.cgi?L(i)<L(i-1)" alt="L(i) Alors

Ce critère permet de vérifier que chaque nouvel élément de la série est supérieur ou égal au précédent. Si ce n’est pas le cas, l’algorithme affiche le message :

« Votre série n’est pas ordonnée »

et termine ses vérifications. Cela garantit que la liste est croissante à tout moment du traitement.