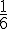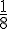Angles orientés et trigonométrie : corrigé des exercices de maths en 1ère en PDF
Mis à jour le 25 novembre 2025
Dans cet article, nous allons explorer les angles orientés et leur application en trigonométrie, des compétences clés pour les élèves de première. La compréhension des angles et de leurs propriétés est essentielle pour maîtriser des concepts mathématiques plus avancés. Les exercices corrigés que nous vous proposons ici permettront aux étudiants de renforcer leurs compétences en géométrie et en analyse tout en se préparant efficacement pour leurs examens.
Exercice 1 – donner plusieurs nombres réels ayant le même point-image.
1) 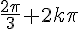
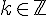
2) 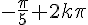
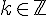
3) 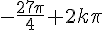
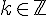
4) 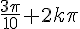
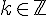
1) 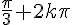
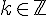
2) 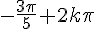
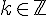
Exercice 2 – convertir les mesures des angles orientés.
1) Conversion des angles en degrés :
a) 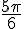
Conversion : 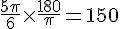
b) 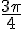
Conversion : 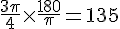
c) 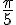
Conversion : 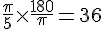
d) 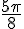
Conversion : 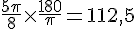
e) 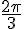
Conversion : 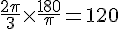
2) Placement sur le cercle trigonométrique :
Les angles convertis étant de 150°, 135°, 36°, 112,5°, et 120°, ils doivent être positionnés respectivement
sur le cercle trigonométrique en respectant ces mesures à partir de l’axe des abscisses positif.
Exercice 3 – cercle trigonométrique et angles orientés.
1) Convertir les mesures des angles orientés suivants en degré :
Conversion de 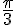
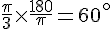
Conversion de 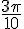
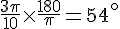
Conversion de 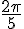
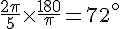
Conversion de 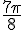
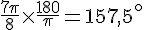
Conversion de 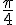
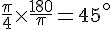
2) Placer sur le cercle trigonométrique les points-images des nombres réels précédents :
Sur le cercle trigonométrique, les angles convertis sont placés comme suit :
- 60° : À
- 54° : Un peu avant
- 72° : Un peu après
- 157,5° : Presque à la moitié de cercle (mi-chemin entre 90° et 180°).
- 45° : À
Exercice 4 – placer les point-image sur le cercle trigonométrique.
Pour placer les points-image sur le cercle trigonométrique, il faut d’abord réduire chaque angle modulo 2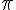
1. 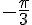
2. 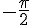
3. 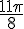
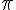
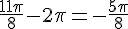
4. 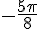
5. 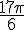
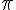
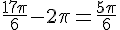
Conclusion : Chacun de ces angles a été décrit par rapport à sa position sur le cercle trigonométrique.
Exercice 5 – représenter l’arc de cercle sur le cercle trigonométrique.
1) Intervalle : ![\left[-\frac{\pi}{4};0\right]](https://maths-pdf.fr/latex-images/11059dc4599e018ddfba881d9f558c65.png)
L’arc de cercle correspondant part de 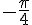
2) Intervalle : ![\left[\frac{\pi}{2};\frac{3\pi}{4}\right]](https://maths-pdf.fr/latex-images/234bd3b083e58a19b282c0360d2e72e7.png)
L’arc de cercle correspondant part de 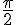
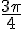
3) Intervalles :
![\left[\frac{\pi}{2};\frac{5\pi}{4}\right]](https://maths-pdf.fr/latex-images/9cbf2fd4d664d93cd509ff5497047976.png)
L’arc de cercle part de 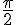
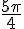
![\left[\frac{7\pi}{4};2\pi\right]](https://maths-pdf.fr/latex-images/eb891a20ce95bd568271485c5dcb1832.png)
L’arc de cercle part de 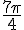
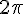
4) Intervalles :
![\left[-\frac{2\pi}{3};-\frac{\pi}{6}\right]](https://maths-pdf.fr/latex-images/b236c88f6e2406763047d7917228dde8.png)
L’arc de cercle part de 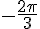
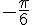
![\left[0;\frac{\pi}{2}\right]](https://maths-pdf.fr/latex-images/df31595eb7cc7d448b762e9319ef6fae.png)
L’arc de cercle part de 0 à 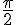
Exercice 6 – donner la mesure des angles orientés.
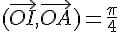
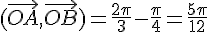
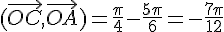
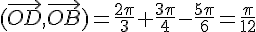
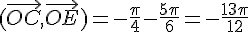
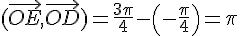
Exercice 7 – angles orientés dans un carré.
1) 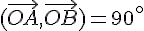
2) 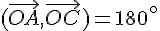
3) 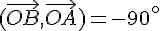
4) 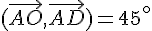
5) 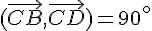
6) 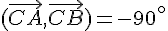
Exercice 8 – mesure principale d’un angle orienté².
Réponse 1 :
La mesure principale d’un angle est obtenue en ajoutant ou soustrayant un multiple de 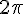
![]-\pi,\pi]](https://maths-pdf.fr/latex-images/9ece7b81376ff59f9430421b04933a11.png)
Pour 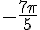
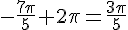
Réponse 2 :
Pour 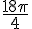
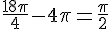
Réponse 3 :
Pour 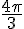
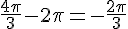
Réponse 4 :
Pour 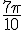
![]-\pi,\pi]](https://maths-pdf.fr/latex-images/9ece7b81376ff59f9430421b04933a11.png)
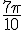
Exercice 9 – mesure principale d’un angle.
1) Pour trouver la mesure principale de l’angle 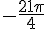
un multiple entier de 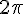
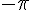
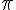
Commençons par simplifier :
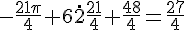
Ensuite, soustrayons 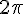
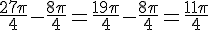
Une nouvelle soustraction est nécessaire :
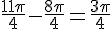
La mesure principale est donc 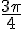
2) Pour l’angle 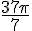
Même démarche :
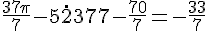
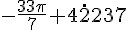
La mesure principale est 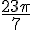
3) Pour 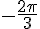
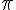
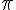
Donc, la mesure principale est 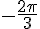
4) Pour 
Simplifiez :
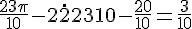
La mesure principale est 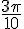
Exercice 10 – vecteurs et mesure principale d’un angle orienté.
1) 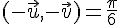
2) 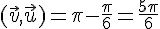
3) 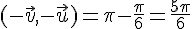
4) 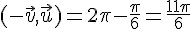
Télécharger ou imprimer cette fiche «angles orientés et trigonométrie : corrigé des exercices de maths en 1ère en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.