Fonctions usuelles : corrigé des exercices de maths en 1ère en PDF
Mis à jour le 25 novembre 2025
Exercice 1 – fonctions carré et inverse.
1. La fonction 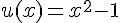
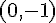
2. La fonction 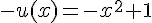
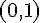
3. La fonction 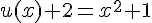
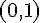
4. La fonction 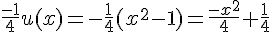
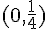
Exercice 2 – logiciel de géométrie et distance minimale.
1) a) Utilisez un logiciel de géométrie dynamique comme GeoGebra pour tracer la courbe 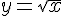
b) En déplaçant le point M le long de la courbe, vous constatez visuellement que la distance AM est minimale
lorsque M se trouve à un point particulier, proche de l’origine.
2) Pour vérifier que 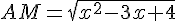
On a 
La distance AM est donnée par :
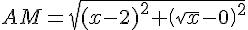
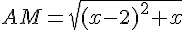
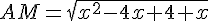
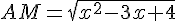
3) Pour minimiser 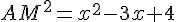
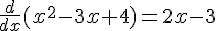
En posant la dérivée nulle, 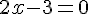
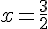
La position de M pour laquelle AM est minimale est donc 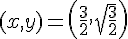
Exercice 3 – tableau de variation et images.
1) 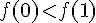
2) 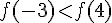
Les valeurs de 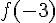
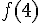
3) 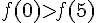
Les valeurs à 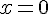
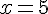
4) 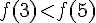
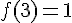
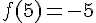
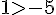
5)
La valeur 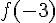
6) 
La valeur 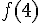
Exercice 4 – préciser le sens de variation des fonctions usuelles.
1) La fonction 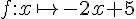
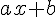
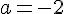
Comme 

2) La fonction 
Elle est décroissante sur ![\left]-\infty;0\right]](https://maths-pdf.fr/latex-images/972439ed03a624db8d0c06cd285a7a00.png)
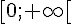
3) La fonction 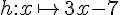
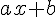
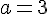
Comme 

4) La fonction 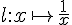
- Sur
- Sur
Exercice 5 – comparer des nombres sans les calculer.
1) Comparons 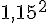

Comme 

2) Comparons 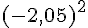
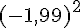
Puisque 
3) Comparons 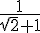
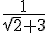


4) Comparons 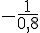
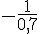


Exercice 6 – résoudre des équations et des inéquations.
1) Résoudre les équations suivantes.
1) Équation : 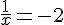
Solution : 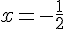
2) Équation : 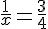
Solution : 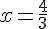
3) Équation : 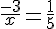
Solution : 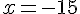
2) Donner un encadrement de 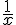
1) Intervalle :
Encadrement : 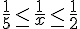
2) Intervalle : 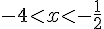
Encadrement : 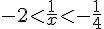
3) Intervalle :
Encadrement : 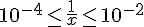
4) Intervalle : 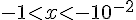
Encadrement : 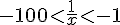
3) Résoudre les inéquations suivantes en s’aidant du graphique.
1) Inéquation : 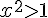
Solution : 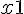
2) Inéquation : 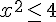
Solution :
3) Inéquation : 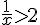
Solution : 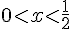
4) Inéquation : 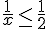
Solution :
Exercice 7 – fonction racine carrée et valeur absolue.
A. Calculer l’image par la fonction racine carrée :
1) 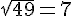
2) 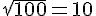
3) 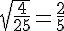
4) 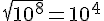
5) 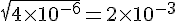
B. Donner les antécédents éventuels :
1) 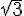
2) 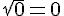
3) 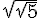
4) Pas d’antécédents car 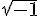
5) 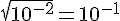
C. Calculer :
1) 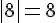
2) 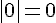
3) 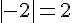
4) 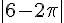
5) 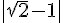
D. Donner la valeur absolue des nombres suivants :
1) 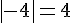
2) 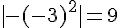
3) 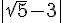
4) 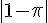
5) 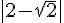
6) 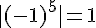
Exercice 8 – valeur absolue et inverse.
1) Résoudre 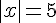
2) Résoudre 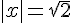

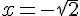
3) Résoudre 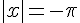
Équation impossible car la valeur absolue ne peut pas être négative.
Compléter par < ou > :
1) 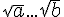
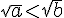
2) 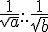
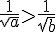
3) 
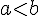
4) 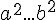
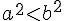
5) 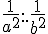

6) 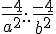
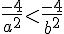
7) 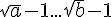
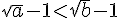
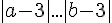
8) 

9) 

10) 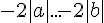
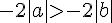
Exercice 9 – fonction linéaire, affine et inverse.
1) Soit u une fonction croissante sur un intervalle I.
Donner le sens de variations des fonctions suivantes sur I :
1) u – 2 : croissante (transformation par translation verticale)
2) u + 3 : croissante (transformation par translation verticale)
3) -3u : décroissante (transformation par multiplication par un nombre négatif)
4) -7u : décroissante (transformation par multiplication par un nombre négatif)
5) -2u + 8 : décroissante (transformation par multiplication par un nombre négatif et translation)
6) 4u – 1 : croissante (multiplication par un nombre positif et translation verticale)
2) Soit u une fonction strictement positive et décroissante sur un intervalle I .
Donner le sens de variations des fonctions suivantes sur I :
1) 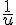
2) 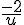
3) 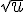
Exercice 10 – encadrement d’un nombre.
Comparaison :
1) Comparons 0,3, 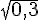
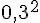
On sait que : 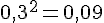
Donc, 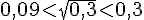
2) Comparons 1,2, 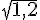
On sait que : 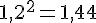
Donc, 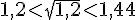
Encadrement de 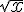
1) 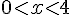
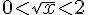
2) 
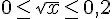
3) 
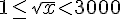
Encadrement pour d’autres expressions :
1) 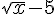
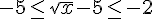
2) 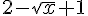
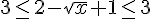
3) 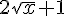

Comparaison de X et Y :
On pose 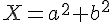
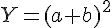
Alors, 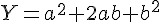
Donc, 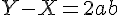
Étant donné que a et b sont positifs, 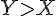
Encadrement de 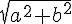
En utilisant le sens de variation de la fonction racine carrée, nous avons :
Puisque 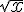
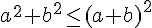
Donc, 
Télécharger ou imprimer cette fiche «fonctions usuelles : corrigé des exercices de maths en 1ère en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.

![\left]-\infty;0\right[](https://maths-pdf.fr/latex-images/7e6feadc670b8adae18546047dd88a8a.png)
![\left]0;+\infty\right[](https://maths-pdf.fr/latex-images/15948b6f0ddb5294659d3d275327982c.png)









